
台形の面積を求めなさい。
本屋さんで母校の赤本を見つけた。
高校の赤本じゃん。
ちょっと覗いたろ。
社会のページを見た。
何これ……。わからん。
母に思わず「私、入学できない!」とひと言。
母は「中学受験とまた内容違うし、
てか無事卒業したからいいのよ。」
私は中学受験をしたので高校受験は体験していない。中学受験では算数・国語・理科のみで、
社会がなかった。
それでも、ものすごく難しかったのを覚えている。
父に固いものでぱこーんと殴られて
泣きながら勉強していた。
数学を見てみよう。
「右の図の台形の面積を求めなさい。」
台形の面積?そんなの小学生で学ぶやつやん。
(上辺+下辺)×高さ÷2やろ?
そんな簡単な問題が高校受験で出るんや。

あれ?高さがなーーーい!
本屋さんでもやもやした私は台形の4辺の長さを記憶し、家で解くことにした。
高さがわかったらいいんだ。
高さ、高さ……と直角に引いてみた。
何にも思い浮かばない。
今どきの中学生ってこんな高度なことしてるの?
いや、私も元理系だったのよ!
きっと解けるはず……
きっと高さを求めるのがこの問題の核なんだ。
2本の線を引いて気づいた、
あっ、ピタゴラスの定理を使えば……。

直角三角形の時の3辺の関係の定理である。
おそらく中学生で学んでいるはず…
わからない長さをx,y,zで表してみる。

これで連立方程式を立てれば…!
連立方程式は求めたい値がいくつかあっても
その数の分、式を作れれば求められる。
例えばこの場合、わからない値がx,y,zとあるけど、
3つ式が作れれば問題ないのだ。
おお、作れたぞ……!

試験のときはもっと簡単でいいでしょう。
あとはこれを解けばいいんだ!!
私の心は踊った。
まずはzを消して、xとyだけの式にしよう。
十うん年ぶりに代入という言葉を使う。
代入とはある式を、他の式に当てはめることである。

二乗が邪魔くさいね…
xの二乗とyの二乗の合計なら①でわかっている。
そうすれば②の式は厄介な二乗が消える!

yとzの関係の式はめちゃくちゃ単純だったから、
zもすぐに出る。
あとはxの値だ!!いや、楽しいじゃんか。

どちらの式にも代入することによって
計算間違いしていないことの確認ができる。
ん?ルート??
ルートの意味はわかる。
平方根といって、二乗してaになる値である。
わかりやすく言えば、正方形の面積がaだった場合の1辺の長さだ。√aという具合に。
√4なら2だし、√9なら3だ。
では√48は?
連立方程式からxつまり台形の高さが
この値ということはわかる。
しかし√48のまま使って答えを出すのは不正解だ。
√8は2√2ってことは、何となく覚えてるんだけど、
√48ってどうやって出すの?
私はググることにした。
もちろんケータイを出した時点で不合格だ。
しかし私はもう随分前にこの高校を卒業している。
受験勉強をするためにこの問題を解いてるわけじゃない。今のままじゃ、モヤモヤしかしない。
ググった結果がこれだ。

たぶん3ヶ月ぐらいしたらまた忘れるだろう。
少し省略しているのでわからない方はググってください。
これでやっと台形の高さが求められた。
これを踏まえて台形の面積
(上辺+下辺)×高さ÷2に当てはめる。
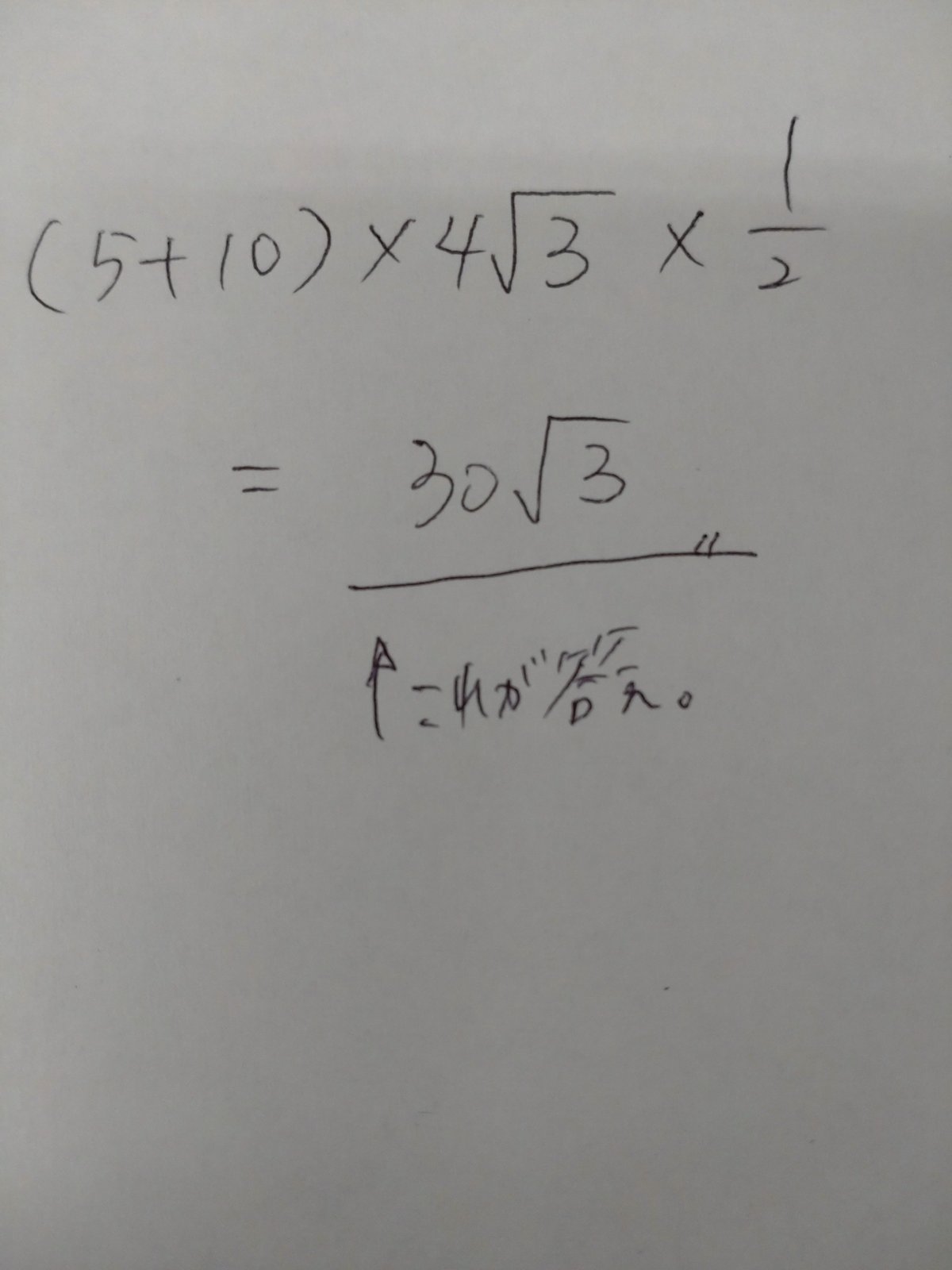
できた〜
解けた〜〜!!
何だかうれしくなった。
台形の面積って、
4辺の長さがわかったら求められるんだ〜!
一見難しいものも、
1つずつ考えると答えに辿り着く。
何だか人生みたいではないか。(大げさ?)
もしかしたら、別の解き方があって、
もっと早く解けるのかもしれない。
でもいろんな手段を使って、解答に導く体験は
スッキリしたし、何より楽しかった。
やっぱりチャレンジは大切だな!
※もし「答え間違ってるよ?」って気づいた方は
ご指摘お願いいたします。
P.S.二乗とか数式とかをスマホ入力は難しかったので、手書き使いました。字が汚いのがバレる…!
数学の先生ってどうやって教材作ってるのかな。。
