
【高校数学】特性方程式のαが謎
皆さんこんにちは!
日常の中で様々なことに疑問を持ち、学んでいっているのですが、せっかくなのでそれを発信していき、共有していこうと思っている、そんな企画でございます。
今回は数学Bの漸化式における特性方程式についてです。
前回の記事では漸化式について扱いました。("ぜんか"をかけたダジャレ)
その中で2つの疑問を紹介しました。
①漸化式の解き方は習ったけど、どうしてそうやって解くの?
②途中で出てくる特性方程式のαって何なの!!
今回の記事ではこの内の②の方を解説していきたいと思います。
たくさん勉強して漸化式に慣れていきましょう!
前回までのあらすじ・・・
非常に難解な数列に直面した時、
「等比数列の形を利用する」という夜神月もびっくり天才的な発想で解決することができました。
その際に皆さんが変形しようとした理想形
![]()
この形に変形するためにαを探す旅に出かけました。
・・・
紆余曲折あってαを見つけることができた皆さん
![]()
ってなんでやねーーーーーん!!!!

こんな風に思いませんでしたかね?
僕は結構謎だったんですよ。
結論
結論から言うと、
![]()
あくまでαは「置き換えた」数なのです。
「いや、それがわけわかんねぇよ!」
という方のために次の項からより詳しく説明していきますね。
とにかく大事なのは
たまたまα=pα+qの形になった
ということ!
特性方程式参上!!
理系に興味のない、生まれながらにして数学アレルギー持ちのU子。
今週唯一の楽しみであった体育を終えた6限の数学B…
襲い来るのは漸化式
それを解くために必要と言われた特性方程式…
ガビーン!!
「二次方程式でギリだったのに…大体、なんで看護学部志望なのに数学Bまでやらなきゃいけいないのよ…トホホ…」
日本の全看護学部受験生が感じていることであります。
この特性方程式って言葉はあまり正式なものではないらしく、Wikipediaにも「特性方程式」というページは存在しませんでした。
特性方程式というのは簡単に言うと、
ある式を解くための手助けをしてくれる式
というような意味になります。
まぁお助けキャラってとこですかね?

とても任天堂の公式ホームページとは思えないようなホームページ
昔はこれが普通でした
なので、突然出てきて、何事もなかったかのように去っていく存在だったのです。
高校の範囲では、漸化式を解くために登場します。
他にも特性方程式が登場する場面があり、
例えば微分方程式という訳の分からない式を解くためにも出てくるので、物理学をやりたい人は覚悟しておいてください。
そもそも何で急にα?
話は少し戻って、
皆さんは与えられた漸化式を解かなくてはいけませんでした。
その際に考えたのが、
![]()
ということ。
何でこうしたかというと、要するにこの式は
![]()
とすると、
![]()
ということであり、これはbの等比数列だったんですね。
初項も公比もわかっているので、等比数列だったらもう解けるはずなのです。
残念ながらもう「いやいや、等比数列って何よ???」って人は着いて来れないような領域まで来てしまったのです・・・
申し訳ありませんが、等比数列は分かっていること前提で行かせてもらいます。
![]()
というのは、
「こういう式に変形することができれば解けるのになー」
という理想的な形を持った式だったのです。
で、我々は今からそのαの正体を探す旅に出るわけなのです。
(ここから先の漸化式の解き方は前回の記事で解説しているので、今回はαの求め方の説明のみになります)
αを探せ!!
はい!
ということで、早速αがどんな数字なのかを検証していきましょう!!
まず、皆さんが何をしたかったかというと、
![]()
という難解な式を解くために、
![]()
という解くことのできる形に直したいと思ったわけでございます。
ここで、②の式をちょっといじっていきましょう。
![]()
左辺のαを右辺に移項した
![]()
右辺を展開した
そしてここで"左"辺に注目してみてください!
①の式と同じですね。
ということは"右"辺も同じでなくてはならないのです。
すなわち、
![]()
こういうことですね。
この式をまた変形してやると・・・
![]()
両辺の同じ記号は削除
![]()
移項して左右を入れ替えて
完成!!!
ちょっとちょっと!
みなさんよく見てくださいよ!
なんとこの式、一番最初に解きたかった問題
![]()
から
![]()
と言えないですか?
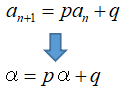
ね?
あとは実際の問題ではpとqはわかっているわけですし、そのわかっている数字を代入したやればαが求まります。
αが求まるということは、晴れて問題の漸化式が解けるというわけです。
そして、このα=pα+qというのが「特性方程式」と言われるおたすけキャラとなのです。
偶々
こんな感じで「置き換え」ることでαが求まるのです。
そして、そっくりそのまま置き換えてOKなのはある意味たまたま。
偶然そうなっただけというわけです。
偶然にしては非常にわかりやすい式ですし、これは「αに置き換えればいいよー」と教えたくなっちゃいますよね。
(必然的にこうなるようなカラクリがあるのかもしれませんが)
今回の説明を完璧に理解しなくても
「たまたまこの形で解けるんだな~」
くらいの認識を持っていただければ結構かと思います。
少しでも疑問が軽減できればそれでオッケーなのです!
本日はここまで!!
補講
とは言ったものの、
頭のいい人の中にはこんな疑問を持つ方もいるでしょう。
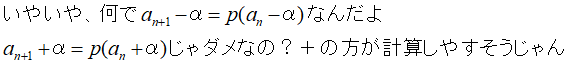
確かにその通りでございます。
では、-αを+αに変えてαを求めてみましょう。
そうするとこうなります。
![]()
pとqは問題文に書いてあるはずなので、これでαが求められます。
そうして見つかったαを
![]()
に代入してやれば解けるのです。が、
![]()
ってなんだか覚えづらいですよね。
というよりも
![]()
って元の問題の式とそっくりでとっても覚えやすいです!
恐らくこれが-αにしている理由なんだと思います。
細かい求め方を理解できていれば-αでも+αでも関係ありません。
どちらでも答えは一緒です。
めでたしめでたし
さぁ!謎は解けましたか?
すっきりしたでしょうか?
要するに「いい感じにこういう形になったんだよ~」ってだけだったんですね。
もう文句言わずに使えるものは使いまくっちゃいましょう!!
ということで今回はここまで。
今回の記事がためになったという方、面白かったという方はぜひSNS等でシェアしてくださると嬉しいです。
間違いがあったりしたらコメント等で教えてください。
また、「お疲れ!コーヒーでも飲みな!」という方はサポートをしてくださるととても励みになります!
また、他の記事もぜひ見てみて、ついでにTwitterのフォローもお願いします!!⇒https://twitter.com/mazenemaze
それでは、また次回の記事でお会いしましょう!!
