
【夏休み企画】おすすめ自由研究3選 数学編
どうも皆さまこんにちは!LITの数学担当、Taroです!夏休みですね!!!
これから夏休みに入っていく中、夏休みの課題に苦心する方もいるのではないでしょうか?
今回の夏休み企画では、私たちLITのメンバーたちがそれぞれいろんなトピックについて語っていきます。
まだ、最初の記事や、前回の記事をご覧になっていない方は是非読んでみてください!
この記事では「おすすめ自由研究3選 数学編」と銘打って、皆様の自由研究や、学びのお手伝いとなるようなトピックを提供できればなと思います。
それでは、やっていきましょ~!
1.身の回りに潜む数学を追ってみよう!
「いきなり何言ってんだ」とお思いでしょう。実は普段私たちが暮らしているこの世界では、数学がありとあらゆるところに潜んでいます。
そういった「身の回りに潜む数学」をいろいろ調べて、学んでみよう!ということです。「え~、いきなりそんなこと言われても探せないよ~」という方もいるでしょう。
身近に潜む数学の例を2つ紹介したいと思います!
1-1.身の回りに潜む数学 モノを表すn進法
n進法とは、皆様ご存じでしょうか?
本来は高校で習うものです。
n進法について、簡単にご説明しましょう。

例えば、10進法で8521という数を表すならば、
千の位(10³の位)に8という数が入り、百の位(10²の位)に5、十の位(10¹の位)に2、一の位(10⁰の位)に1という数が入ります。(ちなみにこれは素数です。)
詳しい解説はいずれ記事で書くつもりですのでその時にでも!
要は、数字の表し方というイメージでOKです!
実は、このn進法、意外と周りの生活や、意外なところにも使われています。身の回りだとコンピューターであったり(2進法や16進法など・・・)、 時計など(12進法)が挙げられます。
さらに言うと、歴史がお好きな方なら狼煙、SF好きの方ならモールス信号も、見方によっては2進法といえるでしょう。
「なぜ、その数の表し方が都合がよいのか」という研究しても良いかもしれませんね。
1-2.身の回りに潜む数学 ハチの巣の図形、ハニカム構造
私は見たことがありますが、みなさまは「ハチの巣って見たことありますか?」
実はハチの巣の構造って、数学的に美しいんです・・・。
ハチの巣は、断面を見てみると正六角形を敷き詰めた形をしています。
そう、平面に正六角形はきれいに敷き詰められるんです!
(他には、正三角形、正方形があります、これが何故かは証明されているので、それを調べてもいいかも)

この正六角形を隙間なく敷き詰めた構造をハニカム構造といいます。
なんか美しいと私は感じます・・・。
「私が数学にハマった理由」でも述べた通り、数学って芸術なんです。
このハニカム構造、いろんなところに使われています。CDプレーヤーや 一眼レフカメラなどが挙げられます。
なぜこの形が都合がいいのか?はたまた他にどんなところにあるか、調べてみてみるのも面白いと思います!
2.数学者の姿に迫る ~数学の歴史を味わう~
実際の数学は、過去の素晴らしい変人(誉め言葉)たちによって発展してきました。そんな数学者たちが紡いできた歴史を掘り下げたり、数学者たちの意外なエピソードなどを掘り下げるのもまた面白い研究になるのかな、と思います!
ここからは、そんな数学者たちが紡いできた数学の歴史をちょっとだけご紹介させていただきます!
2-1.「0」の起源と、それまでの数学
0という、何もないこと、位に数字がないことを示す数は、正確な時期はわかっていませんが、インドが起源とされています。そもそも、なぜ0がそれ以前考えられなかったのでしょうか?
有名な言葉として、「エジプトは、ナイルの賜物」があります。
毎年のように氾濫するナイル川によって、個人の土地がめちゃくちゃにされてしまい、誰の土地がどこまでか、などが分からなくなってしまうことがありました。
それを”測量”することで土地をもとに戻そうという動きが、エジプトで数学が興った起源であり、図形を数学的に考察する「幾何学」の始まりです。
ちなみに幾何学は英語で、「Geometry」といいますが、Geo=土地、
Metry=測ることなので、幾何学とは、土地測量学という意味になります。
エジプトの数学幾何学では、なぜ0がなかったのでしょうか?
それは、長さが0の直線や、高さや底辺が0の三角形などを考慮していなかったからと言われています。エジプトにおいて、発展していた幾何学は、0を考える必要がなかったのです。

つまり、インドの数学は、エジプトのそれとはまた違ったものになっていきます。そういった歴史を追うのもまた面白いかもしれませんね!
3.直感と違った数学。あなたの直感本当ですか?
さて、最後は、あなたの「直感」を裏切るかもしれない、そんな数学の事実についてです。数学はしばしば、私たちの想像を超える真実を導き出すことがあります。
また、数学をうまいこと使うことで、その人の印象をガラリと変えてしまうことだって可能です。
そんな数学の例について軽くお話していきたいと思います。
3-1.その扉。変える?変えない? ~モンティ・ホール問題~
モンティ・ホール問題とは、アメリカのゲームショー番組である、
「Let's make a deal」という番組で出された問題です。
あまりにも直感と違う事実が確率論で示されたことで、モンティ・ホール・ジレンマ、モンティ・ホール・パラドックスとも称されているそう。
皆さんも、実際考えてみてください。
問)
あなたの前に閉じた3つのドアがある。
1つのドアには景品が、2つのドアには、はずれがある。
あなたは景品のドアを当てると景品がもらえる。
あなたが1つのドアを選んだ後、残りのドアのうちはずれがあるドアを 開けてはずれであることが示される。
ここであなたは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。
ここであなたはドアを変更すべきか?
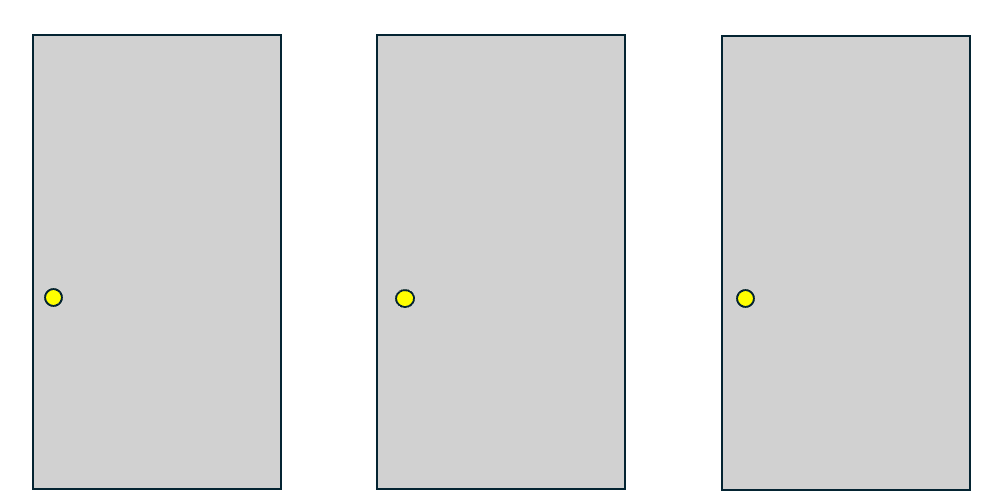

さて、これを変更するかしないか、はたまた変更しても変わらないのか・・・・この答えが、世紀の大論争を起こしてしまったのです!
皆さんはどう思いましたか?
あなたの直感が果たしてあっているのか!?その答えは、ぜひ、皆さんが研究してみてください・・・!!
4.まとめ
いかがでしたでしょうか?今回は、数学でおすすめできる自由研究3選という形で、3つの視点からの研究を紹介させていただきました。
ここに紹介した研究を使って深めてみるもよし、ここの例にはないことを研究してみるもよしです!ここまでお読みくださり、ありがとうございました!
夏休み企画第7弾をお楽しみに!!
お問い合わせ先
記事のご感想については、各記事のコメント欄にご記入ください。
また団体に関するご質問やご相談については下記のメールアドレスからご連絡いただけると幸いです。
メールアドレス
lightupyourtorch@gmail.com
