項目反応理論(IRT)における受験者の学力推定方法のイメージ
はじめに
こんにちは、ライフイズテックでデータサイエンティストをやっているホンディーです。今回も項目反応理論について記事を書きます。
ライフイズテックではサービスを導入いただいた学校や塾の生徒の皆さんに良い教材を提供するため、作成している問題の質の評価に項目反応理論を活用することが多くあります。しかし、世間一般的には項目反応理論はテストの受験生の学力の評価に用いるものです。そして昨今は項目反応理論が導入された資格試験等もあるので皆さんの関心もそちらの方にあるのではないかと思います。
そこでこの記事では、項目反応理論を用いたテストでは受験者の学力がどの様に評価されるのか、ということを単純な例を使って説明したいと思います。項目反応理論の中にもいくつか流儀がありますがここではベイズ推定の事後確率最大推定(MAP推定)を取り上げます。
問題ごとに配点があって正解した問題で獲得した点数を合計していく従来の採点方法とは全く違うやり方である、という点を感じていただけるといいなと思います。
ベイズの定理
項目反応理論において最重要な働きをするのが、ベイズの定理です。
$$
P(A|B) = \frac{P(B|A)P(A)}{P(B)}.
$$
各記号の意味は次のようになります。
$${P(A|B)}$$: 事象Bが起きた場合に事象Aが起きる確率
$${P(B|A)}$$: 事象Aが起きた場合に事象Bが起きる確率
$${P(A)}$$: 事象Aが起きる確率
$${P(B)}$$: 事象Bが起きる確率
雑に言うと、ベイズの定理を使うと Aである場合にBが起きる確率から、Bである場合にAが起きる確率を計算できるのです。
例えば項目反応理論では、生徒の学力が$${\theta}$$であるとわかっているとき、困難度などのパラーメータがわかっている問題に対する正解率が算出できます。そこにこのベイズの定理を使うとそれを反転させて、その問題の採点結果からその受験生の学力が$${\theta}$$である確率を算出できるというイメージです。
単純化した設定における学力パラメーターの推定例
架空のテストと架空の採点結果を元に、実際に学力を推定してみましょう。
ここではより話を単純にし、積分を使わずに説明するために生徒の学力パラメーター$${\theta}$$は、 $${-1, -0.5, 0, 0.5, 1}$$ の5種類の値のどれかだと仮定します。(本当は$${-\infty \sim \infty}$$の実数値を取ります。)
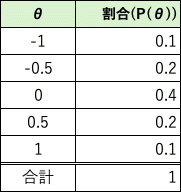
更に、生徒全体の学力パラメーター$${\theta}$$の分布は次表のとおりだと仮定します。要するに平均的な学力の生徒が一番多くて、極端に高かったり低かったりする生徒は少ないよね、という自然な前提をおいておきます。これを事前分布と言い、先程のベイズの定理の$${P(A)}$$に相当するものです。ここではAではなく$${P(\theta)}$$と書きましょう。
そして、とある生徒が解いた問題のパラメーターと正誤の結果を次のように仮定します。5問回答して4問正解し、一番難しいものを間違えています。ここからこの生徒の学力を推定していきます。

上の表の採点結果 {正解, 正解, 正解, 正解, 不正解}を、$${\mathbf{u}}$$ と書くことにします。つまり$${P(\mathbf{u})}$$は採点結果が {正解, 正解, 正解, 正解, 不正解}となる確率だし、$${P(\mathbf{u}|\theta=0)}$$は、学力$${\theta}$$が0の生徒の採点結果が{正解, 正解, 正解, 正解, 不正解}となる確率です。
さて、該当の受験生の学力はまだわかりませんが、$${\theta}$$の値を$${-1, -0.5, 0, 0.5, 1}$$ のどれかに仮定すると、それぞれの問題に正解できる確率は項目特性曲線の式から計算できます。念の為、以前の記事で紹介した計算式を再掲しておきます。
$$
p_j(\theta_i) = \frac{1}{1+e^{-Da_j(\theta_i-b_j)}} \qquad(D=1.701).
$$
更に、各問題の正解率がわかると、全体の採点結果が$${\mathbf{u}=}$${正解, 正解, 正解, 正解, 不正解}となる確率もわかります。
{問題1の正解率 ✕ 問題2の正解率 ✕ 問題3の正解率 ✕ 問題4の正解率 ✕ 問題5の不正解率} を計算すればよいのです。問題5の不正解率は {1-正解率}で出せますね。これが$${P(\mathbf{u}|\theta)}$$です。
5個の$${\theta}$$と5問の問題についてそれぞれの正解率と、$${P(\mathbf{u}|\theta)}$$を計算した結果が次の表です。

この時点でベイズの定理を使う部品として事前分布$${P(\theta)}$$と、各学力の生徒の採点結果が$${\mathbf{u}}$$になる確率の$${P(\mathbf{u}|\theta)}$$が揃いました。あと必要なのは学力を仮定せずに採点結果が$${\mathbf{u}}$$になる確率$${P(\mathbf{u})}$$ですが、これは次の式で計算できます。
$$
P(\mathbf{u}) =\sum_{\theta \in \{-1, -0.5, 0, 0.5, 1\}} P(\mathbf{u}|\theta)P(\theta).
$$
そしてこれを計算した結果は約$${0.088}$$です。
部品が全部そろいましたので次のベイズの定理が使えます。採点結果が$${\mathbf{u}}$$だった場合に学力パラメーター$${\theta}$$である確率をそれぞれの$${\theta}$$について計算してみましょう。
$$
P(\theta|\mathbf{u}) = \frac{P(\mathbf{u}|\theta)P(\theta)}{P(\mathbf{u})}.
$$
結果がこちらの表です。ちなみにこの一番右の列の$${P(\theta|\mathbf{u})}$$を事後分布と言います。

この表から、採点結果がu = {正解, 正解, 正解, 正解, 不正解} である場合に、その生徒の学力$${\theta}$$が-1である確率は 0.005で、0.5である確率は0.352だ、というように$${\theta}$$の確率分布が得られました。
そして、事後確率最大推定(MAP推定)では、この確率が最大になる$${\theta}$$、上の表で言えば確率が0.352である、$${\theta=0.5}$$ を推定値とします。
以上が、単純化した例におけるMAP推定の計算例でした。項目反応理論における学力の推定のイメージを掴んでいただけたでしょうか。
以降の内容はおまけですが、もう少しだけ周辺の話題をピックアップして取り上げていきたいと思います。
おまけ1. 事後分布の活用例
先程の事後分布の算出結果から、$${\theta=0.5}$$と推定しましたが注意深い方であれば、$${\theta=0}$$の確率は0.312で、$${\theta=1}$$の確率は0.283と、$${\theta=0.5}$$の0.352とかなり僅差である点が気になったかなと思います。
要するにこれは、今回の例のようなたった5問のテストでは精度高く評価できておらず他の値が正しい可能性も除外しきれていないという事象が反映されているのです。この様に、事後分布を確認することでこの推定の精度も一緒に評価できます。
さて、もしこの受験生に追加で問題を出題できるとしたらどのような問題を出題するでしょうか?$${\theta}$$が-1や-0.5である確率はずいぶん低いので、あまり難易度が低い問題を出題する意味はなさそうですね。すると0〜1の範囲の学力の生徒にとってちょうどいい問題を追加したいと考えるのが自然だと思います。
これをコンピューターを使って、その時点までの採点結果から現時点での学力を推定し次の問題を決めていくテストのやり方を、コンピューター適応型テスト(Computerized adaptive test, CAT)と言います。項目反応理論の応用として複数のテストで実際に行われています。
おまけ2. MAP推定以外の方法の紹介
最初に、MAP推定以外にもいくつか流儀があると書きましたので他の方法も少しだけ紹介しておきます。
1つ目は期待事後推定(EAP推定)です。事後分布の期待値で推定します。
先程の例で言えば、次のように計算します。
$$
\sum_{\theta \in \{-1, -0.5, 0, 0.5, 1\}} \theta P(\theta|\mathbf{u}) \fallingdotseq 0.429
$$
もう1つはそもそも事前分布を設定せず、したがってベイズの定理も使わずに、$${P(\theta|\mathbf{u})}$$が最大になる$${\theta}$$を推定値とする方法です。これは最尤推定と言います。
それぞれの方法にメリットとデメリットが有り一概にどれが優れていると言える物では有りません。
アルゴリズムの実装難易度や、データが少ない場合の推論結果の安定性、逆にデータが増えた場合に必要なリソースや計算時間などのコスト等を総合的に判断して最適なものを選ぶ必要があります。
おまけ3. 実際の項目反応理論での計算
今回の例は実際の計算過程をすべてお見せするために$${\theta}$$の値を5種類に限定して話を進めました。しかし実際の項目反応理論では、$${\theta}$$は任意の実数値を取ります。
この場合は事前分布として連続な確率分布、ほとんどのケースで標準正規分布を仮定します。つまり、$${P(\theta)}$$が以下の式となります。
$$
P(\theta) = \frac{1}{\sqrt{2\pi}} e^{-\frac{\theta^2}{2}}.
$$
そして、$${P(\mathbf{u})}$$は$${\Sigma}$$ではなく積分を使って次式で計算します。
$$
P(\mathbf{u}) = \int_{-\infty}^{\infty}P(\mathbf{u}|\theta)P(\theta) d\theta .
$$
この2点を置き換えることで、連続値の$${\theta}$$に対しても事後分布を求めることが可能になります。
おしらせ
ライフイズテック サービス開発部では、気軽にご参加いただけるカジュアルなイベントを実施しています。開催予定のイベントは、 connpass のグループからご確認ください。興味のあるイベントがあったらぜひ参加登録をお願いいたします。皆さんのご参加をお待ちしています!
