
【インド式】11~19までのかけ算
こんにちは! くるくるぼっちです。
今日は、インド式計算の中で、11~19までのかけ算を一瞬で解いてしまう方法です。

計算方法
インド式の計算は、いろんなパターンがあります。
今回は、『分配法則』を使います。
計算式:14 × 17 = ?
1. まず、どっちかの数ともう片方の一の位の数字を足します。
"14" 足す "7" は?
14 + 7 = 21
2. 次に、元の数字の一の位どうしをかけます。
一の位は、 "4" と "7"
4 × 7 = 28
3. 最後に、1 と 2 で出た答えをちょっとズラして足します。
1. 14 + 7 = 21
2. 4 × 7 = 28
"21" と "28" ですね。
ちょっとズラして足すために、筆算にしてみます。
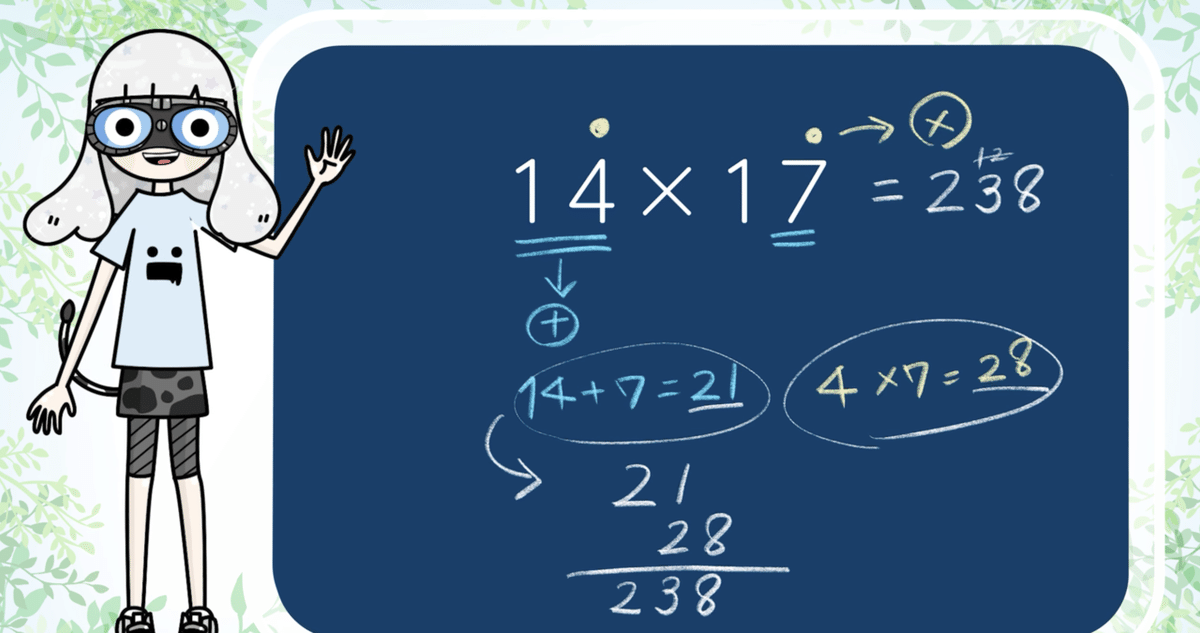
21
28
——
238
こんな感じ!
つまり、"14 × 17 = 238" は "10×21+28=238" と同じということになります。
練習問題
じゃんじゃん、練習に使ってください!
14×16=
18×18=
12×16=
13×17=
19×14=
カラクリ
『1~19までののかけ算が一瞬で解ける方法』のカラクリです。分配法則を使います。
<公式>
(10+a)×(10+b)
=10×10+10b+10a+ab
=10×(10+a+b)+ab
先程の計算式に当てはめてみるとこうなります。
14×17=(10+4)×(10+7)
=10(10+4+7)+4×7
ちょっとややこしかった?
もうちょっとシンプルにしてみました。
AB×CD=10×(AB+D)+(B×D)
これでどやー!
おしまい。
参考資料
いいなと思ったら応援しよう!

