【入試問題解説#3】女子学院中学校（2018年/大問7）

こんにちは。
今回は、中学入試や大学入試の問題解説をおこなっていきたいと思います。

第3回の今回は、中学入試問題を取り上げます。

今回、扱う問題は女子学院中学校の2018年度の入試問題です。

問題

今回、取り上げる問題はこの問題です。

ぜひ、解いてみてください！
目標時間は8分です。

↓↓↓↓↓↓解答・解説↓↓↓↓↓↓

解答

(１)　105
(２)　180・210・475

解説

（１）

食塩水の濃度を考える際には、天秤図を用いるとわかりやすいです。

その際のポイントは、
　食塩水の量の比と濃度の比は逆比であるということです。

2.8%と6.4%の差は3.6%。
6.4%と11.2%の差は4.8%

すなわち、その差の比は３：４になります。

ここで、量と濃度の比は逆比であるので、以下のように考えられます。

すなわち、求める答えは、

　140 × 3/4　＝105（g）

答え：105g

（２）

容器Aに水を□g入れる
　＝食塩の量は変わらない。

それぞれに入っている食塩の量を求める。

＜容器A＞
　300 × 0.112 ＝ 33.6（g）
＜容器B＞
　200 × 0.028 = 5.6（g）

『容器Aに水を□g加えてかき混ぜた後、そこから100gを取り出して容器Bに入れてかき混ぜると4.2%の食塩水ができました。』

この部分を、天秤図に表します。

量の比が２：１なので、濃度の比は１：２の逆比になります。

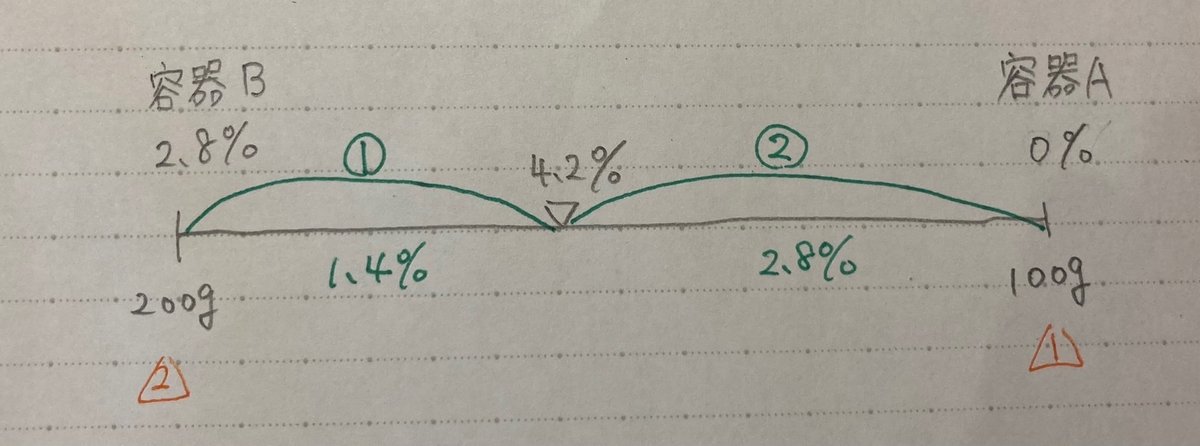
よって、容器Aの濃度は
　4.2 + 2.8 =7.0（%）となります。

容器Aに入っている食塩の量は33.6gですので、それが7%に相当します。

より、
　33.6 ÷ 0.07 = 480（g）

より、容器Aに入っている食塩水の量は480gです。

求める答えは、
　480 - 300 =180（g）

答え①：180（g）

『次に容器Bに入っている食塩水の水を蒸発させて食塩水の重さを□gにした後、そこから95gを取り出して容器Aに入れてかき混ぜると、6.8%の食塩水□gができました。』

この段階の様子を天秤図に表します。

量の比が１：４ですので、濃度の比は４：１の逆比になります。

より、容器Bの濃度は6％であるとわかります。

『容器Aに水を□g加えてかき混ぜた後、そこから100gを取り出して容器Bに入れてかき混ぜると4.2%の食塩水ができました。』

この動作があったので、容器Bに入っている食塩水の量は300（g）で、食塩の量は、12.6gです。

「蒸発」ですので、食塩の量に変化はありません。

よって、12.6gが6%に相当します。

12.6 ÷ 0.06 = 210 （g）

より、蒸発後の食塩水容器Bの食塩水の量は210gであるとわかります。

答え②：210g

最後の答えは、食塩水の量の和です。

左側に95g、右側に380gですので、合計は475gになります。

答え③：475g

まとめ

いかがだったでしょうか。
今回は、女子学院中学校の問題を取り上げました。
女子学院中学校の問題は、難易度自体は高くないものの、スピードが求められる問題が多い印象です。
　
今後も取り上げてほしい問題があれば、コメントにてお伝えください。

最後に

　記事を見つけてくださりありがとうございました。
　よろしければ、フォロー・Likeもお願いします。
　コメントでご意見、感想もお聞かせください。