
Pythonライブラリ(線形代数):Numpy(np.linalg編)
1.概要
Numpyの機能の中でも線形代数(Linear algebra)に特化した関数であるnp.linalgについて紹介します。
基本的なNumpy操作は別記事をご確認ください。
「スカラ・ベクトル・行列・テンソル」の記号は(太字を忘れること多いですができるだけ)下記に従いたいと思います。

2.Numpy操作の基礎
線形代数で必須の部分だけ上記記事から情報を抽出しました。
2-1.Numpy配列:np.array()
Numpyでの配列はnp.array()で生成し、スカラ・ベクトル・行列・テンソルオブジェクトの作成は下記の通りです。
[IN]
import numpy as np
#Scalar(スカラー)
X_scalar = np.array(1)
display(X_scalar)
print(f'次元数:{X_scalar.ndim}, 形状:{X_scalar.shape}')
#Vector(ベクトル)
X_vec = np.array([1, 2, 3])
display(X_vec)
print(f'次元数:{X_vec.ndim}, 形状:{X_vec.shape}')
#Matrix(行列)
X_mat = np.array([[1, 2, 3],
[4, 5, 6]])
display(X_mat)
print(f'次元数:{X_mat.ndim}, 形状:{X_mat.shape}')
#Tensor(テンソル)
X_tensor = np.array([[[1, 2, 3],
[4, 5, 6]]])
display(X_tensor)
print(f'次元数:{X_tensor.ndim}, 形状:{X_tensor.shape}')
[OUT]
array(1)次元数:0, 形状:()
array([1, 2, 3])次元数:1, 形状:(3,)
array([[1, 2, 3],
[4, 5, 6]])次元数:2, 形状:(2, 3)
array([[[1, 2, 3],
[4, 5, 6]]])次元数:3, 形状:(1, 2, 3)2-2.転置行列:np.transpose()
転置行列とは「行列の行と列を入れ替えた行列」です。Numpyメソッドの"np.transpose()"または属性を使用して"array.T"で実行できます。
$$
\mathbf{X}=
\begin{pmatrix} x_{11} & x_{12} & x_{13} \\x_{21} & x_{22} & x_{23} \\ x_{31} & x_{32} &x_{33}\end{pmatrix}->
\mathbf{X^T}=
\begin{pmatrix} x_{11} & x_{21} & x_{31} \\x_{12} & x_{22} & x_{32} \\ x_{13} & x_{23} &x_{33}\end{pmatrix}
$$
[IN]
X = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
#転置行列
X.T #np.transpose(X)と同じ
[OUT]
array([[1, 4, 7],
[2, 5, 8],
[3, 6, 9]])2-3.四則演算・その他基礎演算
各種演算・留意事項は下記の通りです。
●和差商積:numpy配列同士に+, -, *, / で計算可能
●累乗:array**nまたはnp.power(array, 乗数)
●平方根(ルート):np.sqrt(array)
●指数関数・対数関数:np.exp(array)、np.log1p(array)
2-4.標準行列:np.zeros, np.ones, np.full, np.eye
特定の形・数値の配列を作成する場合は下記のメソッドがあります。
●np.zeros(ゼロ行列):すべての値が0の行列を作成
●np.ones(1行列):すべての値が1の行列を作成
●np.full(行列指定):指定した形状・値の行列を作成
●np.eye(単位行列):対角成分のみ 1でそれ以外は 0である正方行列
[In] #ゼロ行列
np_zero1 = np.zeros(3) #形状(3,)の0行列(ベクトル)
np_zero2 = np.zeros([2, 2]) #np.zeros([行数a×列数b])でa×bのゼロ行列
_np = np.array([[1, 2, 3], [4, 5, 6]]) #参考配列:形状(2,3)
np_zero3 = np.zeros_like(_np) #_npと同形状のゼロ行列
[Out] ※print文省略
array([0., 0., 0.])
array([[0., 0.],
[0., 0.]])
array([[0, 0, 0],
[0, 0, 0]])[In] #1行列
np_one1 = np.ones(3) #形状(3,)の1行列
np_one2 = np.ones([2, 2]) #np.ones([行数a×列数b])でa×bの1行列となる。
_np = np.array([[1, 2, 3], [4, 5, 6]]) #参考配列:形状(2,3)
np_one3 = np.ones_like(_np) #_npと同形状の1行列
[Out]
array([1., 1., 1.])
array([[1., 1.],
[1., 1.]])
array([[1, 1, 1],
[1, 1, 1]])[In] #行列を指定
np_full1 = np.full(3,1) #1次元配列:値が1の(3,)行列
np_full2 = np.full([2,3],1) #多次元配列:値が1の多次元配列
np_full3 = np.full([2,3], np.nan) #空行列も作成可能
[Out]
array([1, 1, 1])
array([[1, 1, 1],
[1, 1, 1]])
array([[nan, nan, nan],
[nan, nan, nan]])[In]
np_eye1 = np.eye(2) #np.eye(次元数n)でn×nの単位行列となる。
np_eye2 = np.eye(3, 6) #出力参照
[Out]
array([[1., 0.],
[0., 1.]])
array([[1., 0., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0.]])2-5.ノルム(距離):np.linalg.norm()
ノルムとは「ベクトルの大きさ(距離)」に近い指標でありベクトル$${x}$$をn次元$${x = (x_1,\cdots,x_n)}$$としたときのノルム$${L_{p}}$$は次のように定義されます。
本記事では下記3種のノルムを紹介します。重要なこととして「尺度の異なる数値が組み合われたデータに関する距離の計算は要注意」となります。
$$
{\|\boldsymbol{x}\|_p = \sqrt[p]{|x_1|^p+|x_2|^p+\cdots+|x_n|^p} }
$$
$$
L_{1Norm}(マンハッタン距離) = \sum_{i=1}^{n} |x_i|=|x_{1}|+|x_{2}|+ \dots +|x_{n}|
$$
$$
L_{2Norm}(ユークリッド距離距離) = \sqrt{\sum_{i=1}^{n} x_i^2}=\sqrt{x_{1}^2 + x_{2}^2 + \cdots + x_{n}^2}
$$
【ノルムの種類(参考:高校数学の美しい物語)】
●L0ノルム:ベクトル内における0でない値の数を計算
●L1ノルム(マンハッタン距離):各成分の絶対値の和
●L2ノルム(ユークリッド距離):一般的な距離を意味する。高校数学での三平方の定理でも使われるように長さと同等である。
Numpyでは"np.linalg.norm(<array>, ord=<Norm>)"で計算可能です。
[IN]
A = np.array([[0, 1, -2],
[-3, 4, 5]])
#ベクトルの内積
L0 = np.linalg.norm(A.ravel(), ord=0) #L0ノルム:非ゼロ要素の数※ベクトルのみ
L1 = np.linalg.norm(A.ravel(), ord=1) #L1ノルム:マンハッタン距離
L2 = np.linalg.norm(A.ravel()) #L2ノルム:ユークリッド距離
print(f'L0:{L0:.2f}, L1:{L1:.2f}, L2:{L2:.2f}')
#行列で指定:aixs=0:列方向, axis=1:行方向
L1_ax0 = np.linalg.norm(A, ord=1, axis=0) #L1ノルム:マンハッタン距離
L1_ax1 = np.linalg.norm(A, ord=1, axis=1) #L1ノルム:マンハッタン距離
L2_ax0 = np.linalg.norm(A, ord=2, axis=0) #L2ノルム:ユークリッド距離
L2_ax1 = np.linalg.norm(A, ord=2, axis=1) #L2ノルム:ユークリッド距離
print(f'L1_ax0:{L1_ax0}, L1_ax1:{L1_ax1}, L2_ax0:{L2_ax0}, L2_ax1:{L2_ax1}')
[OUT]
L0:5.00, L1:15.00, L2:7.42
L1_ax0:[3. 5. 7.], L1_ax1:[ 3. 12.], L2_ax0:[3. 4.123 5.385], L2_ax1:[2.236 7.071]$$
A=\begin{bmatrix}0 & 1 & -2 \\-3 & 4 & 5 \\ \end{bmatrix}, A.ravel()=\begin{bmatrix}0 & 1 & -2 &-3 & 4 & 5 \end{bmatrix}
$$
$$
L_{1Norm}=|0|+|1|+|-2|+|-3|+|4|+|5| = 15 \\
L_{2Norm}=\sqrt{0^2 + 1^2 + (-2)^2 + (-3)^2 + 4^2 + 5^2} = \sqrt{55} = 7.42
$$
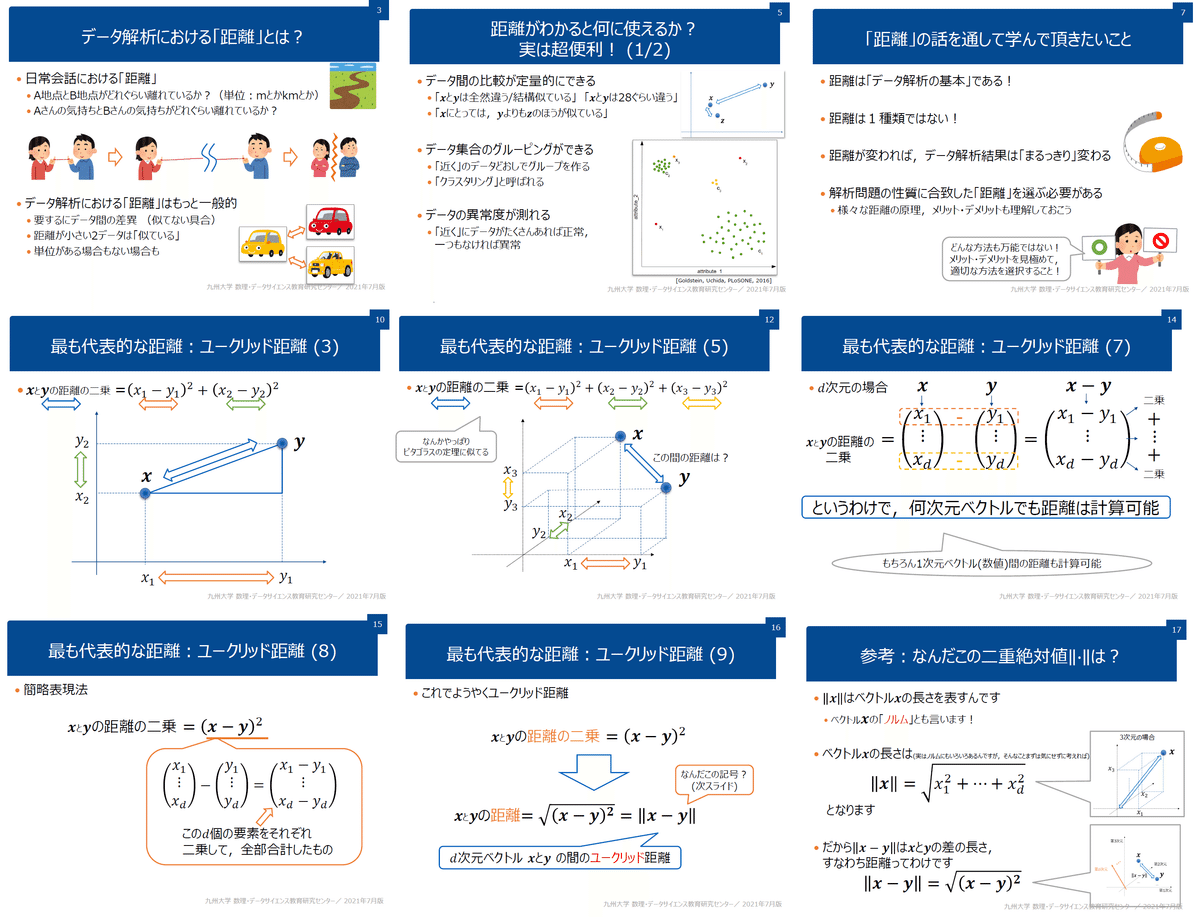
【コラム:ユークリッド距離の補足(データ間の距離と類似度)】

2-6.アダマール積
Numpyでアダマール積を計算する時は掛け算と同じ”*”を使用します。
[IN]
array1 = np.array([[1, 2],
[3, 4]])
array2 = np.array([[10, 20],
[30, 40]])
print(array1*array2) #アダマール積
[OUT]
[[ 10 40]
[ 90 160]]$$
\begin{bmatrix} 1 & 2 \\ 3 & 4 \\
\end{bmatrix}\bigodot\begin{bmatrix} 10&20\\30&40\\\end{bmatrix}=\begin{bmatrix} 1×10&2×20\\3×30&4×40\\\end{bmatrix}=\begin{bmatrix} 10&40\\90&160\\\end{bmatrix}
$$
2-7.内積:np.matmul, np.dot(), @
Numpyで内積を計算する時は3種類の記法があります。コード内で統一しておけば好きな記法で問題ないと思います。
np.matmul(<arr1>, <arr2>):numpyのmatmulメソッドを使用
arr1@arr2:掛け算のように"@"を使用(matmul()と同じ動作)
np.dot(<arr1>, <arr2>):numpyのdotメソッドを使用※状況次第でアダマール積になる可能性がある
arr1.dot(<arr2>):配列のdotメソッドを使用
[IN]
np.matmul(array1, array2)
np.dot(array1, array2) #内積
array1@array2
array1.dot(array2)
[OUT]※3つもと同じ結果
array([[ 70, 100],
[150, 220]])$$
\begin{bmatrix} 1 & 2 \\ 3 & 4 \\
\end{bmatrix}\begin{bmatrix} 10&20\\30&40\\\end{bmatrix}=\begin{bmatrix} 1×10+2×30&1×20+2×40\\3×10+4×30&3×20+4×40\\\end{bmatrix}=\begin{bmatrix} 70&100\\150&220\\\end{bmatrix}
$$
【補足:内積の特性】


2-8.共分散行列:np.cov()
主成分分析などで使用する共分散行列はnp.cov()を使用します。
$$
標本共分散行列 :\large\frac{1}{n}\sum_{i=1}^n (\vec{x}_i-\vec{m})(\vec{x}_i-\vec{m})^T
$$
$$
不偏共分散行列 :\large\frac{1}{n-1}\sum_{i=1}^n (\vec{x}_i-\vec{m})(\vec{x}_i-\vec{m})^T
$$
(n はデータ数、$${\vec{m}}$$ は平均値のベクトル)

3.線形代数の基礎
本節では簡単な用語や数式を記載します。
3-1.線形代数の数式
線形代数でよく使用されるのは内積です。内積を使うと連立方程式を綺麗な形で表現できます。
$$
a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}=y_{1} \\
b_{1}x_{1}+b_{2}x_{2}+b_{3}x_{3}=y_{2}
$$
$$
\begin{bmatrix} a_{1} & a_{2} & a_{3} \\ b_{1} & b_{2} & b_{3} \end{bmatrix} \begin{bmatrix} x_{1}\\ x_{2} \\ x_{3} \end{bmatrix}
=\begin{bmatrix} y_{1}\\ y_{2} \end{bmatrix}
$$
3-2.単位行列:np.eye(n)
単位行列とは対角要素(行列の斜めの要素)が1でそれ以外の要素(費対角要素)が0の正方行列(行と列の数が同じ)です。np.eyeで作成できます。
$$
単位行列I=\begin{pmatrix} 1 & 0 & \dot & 0 \\ 0 & 1 & \dot & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dot & 1\end{pmatrix}
$$
[In]
np_eye1 = np.eye(2) #np.eye(次元数n)でn×nの単位行列となる。
np_eye2 = np.eye(3, 6) #出力参照
[Out]
array([[1., 0.],
[0., 1.]])
array([[1., 0., 0., 0., 0., 0.],
[0., 1., 0., 0., 0., 0.],
[0., 0., 1., 0., 0., 0.]])3-3.置換行列:eye(n)[::-1]
置換行列Pを行列Aにかけると配列が置換されていることが確認できます。置換行列は1種類ではないことはご留意ください。
$$
\begin{bmatrix}0&0&1\\0&1&0\\1&0&0\end{bmatrix}\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}=\begin{bmatrix}a_{31}&a_{32}&a_{33}\\a_{21}&a_{22}&a_{23}\\a_{11}&a_{12}&a_{13}\end{bmatrix}
$$
[IN]
A = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
P = np.eye(3)[::-1]
display(P)
P@A
[OUT]
array([[0., 0., 1.],
[0., 1., 0.],
[1., 0., 0.]])
array([[7., 8., 9.],
[4., 5., 6.],
[1., 2., 3.]])3-4.対角行列:diag()
3-4-1.対角成分の抽出
対角行列とは行列の対角成分であり"np.diag(<array>, k=<対格の位置>)"となります。
$$
A=\begin{pmatrix} a_{11} & a_{12} & \dots& a_{1n} \\a_{21} & a_{22} & \dots& a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \dots& a_{nn}\end{pmatrix}->\begin{pmatrix} a_{11} & a_{22} & \dots& a_{nn} \end{pmatrix}
$$
実行結果は下記の通りです。
np.diag()により行列(2次元)からベクトル(1次元)で抽出
引数kの指定で対角の位置を変更可能
正方行列(n×n)でない場合は最終行までの対角成分を抽出
[IN]
import numpy as np
A = np.array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12],
[13, 14, 15, 16]])
A_diag = np.diag(A)
print(f'元:{A.shape}, diag:{A_diag.shape}')
display(A_diag)
display(np.diag(A, k=1))
display(np.diag(A, k=2))
display(np.diag(A, k=3))
display(np.diag(A, k=4)) #空配列:array([], dtype=int32)
display(np.diag(A, k=-1))
[OUT]
元:(4, 4), diag:(4,)
array([ 1, 6, 11, 16])
array([ 2, 7, 12])
array([3, 8])
array([4])
array([], dtype=int32)
array([ 5, 10, 15])
[IN]
A = np.array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],])
display(np.diag(A), np.diag(A, k=1), np.diag(A, k=-1))
[OUT]
array([1, 6])
array([2, 7])
array([5])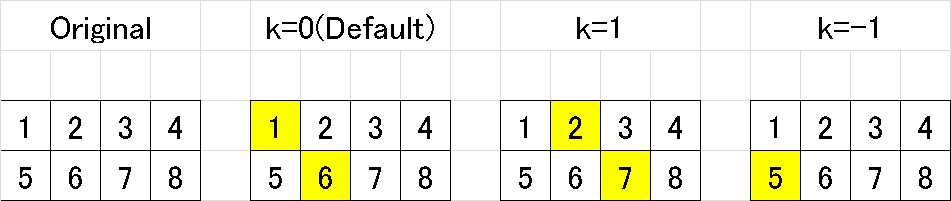
3-4-2.対角行列の作成
対角成分以外(剰余行列R)が0の行列を作成する場合は"np.diag(<1次元array>, k=<対角の位置>)"となります。
$$
A=\begin{pmatrix} a_{11} & a_{22} & \dots& a_{nn} \end{pmatrix} ->np.diag(A)= \begin{pmatrix} a_{11} & 0 & \dots& 0 \\0 & a_{22} & \dots& 0 \\\vdots & \vdots & \ddots & \vdots \\0 & 0 & \dots& a_{nn}\end{pmatrix}
$$
[IN]
a = np.array([1,2,3])
A, A_k1, A_k2 = np.diag(a), np.diag(a, k=1), np.diag(a, k=2)
print(a.shape, A.shape, A_k1.shape, A_k2.shape)
display(A, A_k1, A_k2)
[OUT]
(3,) (3, 3) (4, 4) (5, 5)
前述のメソッドを合わせて使用すれば元の行列から対角成分だけを抽出した行列の作成も可能です。
[IN]
A=np.array([[10, 11, 12],
[13, 14, 15],
[16, 17, 18]])
_array = np.diag(A)
np.diag(_array)
[OUT]
array([[10, 0, 0],
[ 0, 14, 0],
[ 0, 0, 18]])3ー4-3.剰余行列R
剰余行列とは対角成分を除いた残りの行列となります。イメージは下記の通りです。注意点として本記事では「行列A=(L+D+U)になるように分解しているためLとUの対角成分は0」ですが「A=LDUになるように分解する場合はLとUの対角成分は1」となります。
この行列はLDU分解などに使用して反復法などによる微分方程式の数値計算などに使用されます。
A:元の行列、U:上三角行列、L:下三角行列、D:対角行列、R:剰余行列
$$
A=\begin{pmatrix} a_{11} & a_{12} & \dots& a_{1n} \\a_{21} & a_{22} & \dots& a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \dots& a_{nn}\end{pmatrix},D=\begin{pmatrix} a_{11} & 0 & \dots& 0 \\0 & a_{22} & \dots& 0 \\\vdots & \vdots & \ddots & \vdots \\0 & 0 & \dots& a_{nn}\end{pmatrix}
$$
$$
U=\begin{pmatrix} 0 & a_{12} & \dots& a_{1n} \\0 & 0 & \dots& a_{2n} \\\vdots & \vdots & \ddots & \vdots \\0 & 0 & \dots& 0\end{pmatrix}, L=\begin{pmatrix} 0 & 0 & \dots& 0 \\a_{21} & 0 & \dots& 0 \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \dots& 0\end{pmatrix}
$$
$$
剰余行列R=(L+U)=\begin{pmatrix} 0 & a_{12} & \dots& a_{1n} \\a_{21} & 0 & \dots& a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \dots& 0\end{pmatrix}
$$
実際にコードを記載すると下記の通りです。出力は(L+U)の形になっていることが確認できます。
[IN]
A = np.array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12],
[13, 14, 15, 16]])
D = np.diag(A) #対角成分の抽出
R = A-np.diag(D) #剰余行列R
R
[OUT]
array([[ 0, 2, 3, 4],
[ 5, 0, 7, 8],
[ 9, 10, 0, 12],
[13, 14, 15, 0]])
4.線形代数1:基礎編
線型代数(Linear Algebra)はNumpyのlinalgメソッドで計算できます。
4-1.上三角行列・下三角行列:triu(), tril()
上三角行列・下三角行列の概念は下記の通りです。
【上三角行列(upper triangular matrix):対角より左下はすべて0】
$$
U=\begin{bmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ 0&a_{22}&a_{23}&a_{24}\\0&0&a_{33}&a_{34}\\0&0&0&a_{44}\end{bmatrix}
$$
【下三角行列(lower triangular matrix):対角より右上はすべて0】
$$
L=\begin{bmatrix}a_{11}&0&0&0\\a_{21}&a_{22}&0&0\\a_{31}&a_{32}&a_{33}&0\\a_{41}&a_{42}&a_{43}&a_{44}\end{bmatrix}
$$
元の配列Aから対角要素を切り出すことで上三角行列:triu(<行列>, k=<対角の位置>)・下三角行列:tril(<行列>, k=<対角の位置>)を作成できます。
[IN]
A = np.array([[ 1, 2, 3, 4],
[ 5, 6, 7, 8],
[ 9, 10, 11, 12],
[13, 14, 15, 16]])
U = np.triu(A) #上三角行列
L = np.tril(A) #下三角行列
display(U)
display(L)
[OUT]
array([[ 1, 2, 3, 4],
[ 0, 6, 7, 8],
[ 0, 0, 11, 12],
[ 0, 0, 0, 16]])
array([[ 1, 0, 0, 0],
[ 5, 6, 0, 0],
[ 9, 10, 11, 0],
[13, 14, 15, 16]])また引数kを指定してあげることで前述の剰余行列Rを作成できます。
[IN]
U1 = np.triu(A, k=1) #上三角行列
L1 = np.tril(A, k=-1) #下三角行列
display(U1, L1, U1+L1)
[OUT]
array([[ 0, 2, 3, 4],
[ 0, 0, 7, 8],
[ 0, 0, 0, 12],
[ 0, 0, 0, 0]])
array([[ 0, 0, 0, 0],
[ 5, 0, 0, 0],
[ 9, 10, 0, 0],
[13, 14, 15, 0]]
array([[ 0, 2, 3, 4],
[ 5, 0, 7, 8],
[ 9, 10, 0, 12],
[13, 14, 15, 0]])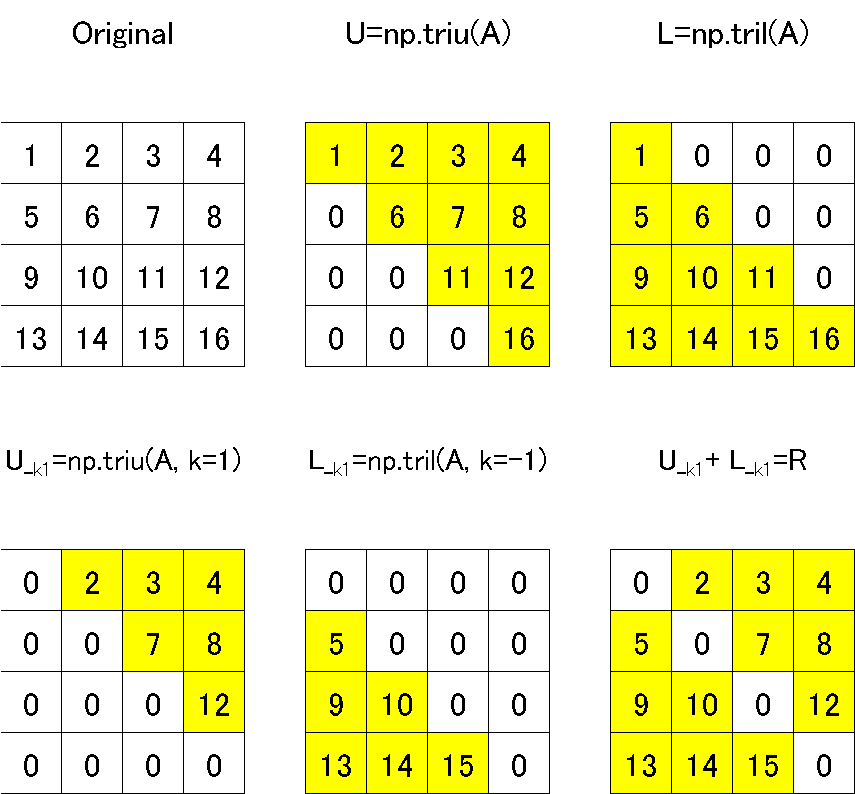
なおtriu(), tril()は元の行列を切り抜いているだけであり後述する「LU分解」とは異なります。
[IN]
display(L@U) #LとUの積:元の行列Aには戻らない
[OUT]
array([[ 1, 2, 3, 4],
[ 5, 46, 57, 68],
[ 9, 78, 218, 248],
[ 13, 110, 302, 600]])4-2.逆行列:linalg.inv()
逆行列 (inverse matrix)とは行列Aに対して$${AA^{-1}=単位行列I}$$となる$${A^{-1}}$$を言います。
$$
\begin{bmatrix} 1 & 2 \\ 3 & 4 \\
\end{bmatrix}
\begin{bmatrix} -2 & 1 \\ 1.5 & -0.5 \\\end{bmatrix}
=\begin{bmatrix} (1×-2+2×1.5) & (1×1 + 2×-0.5) \\ (3×-2+4×1.5) & (3×1+4×-0.5) \\\end{bmatrix}
=\begin{bmatrix} 1 & 0 \\ 0 & 1 \\
\end{bmatrix}
$$
[In]
import numpy as np
A = np.array([[1, 2],
[3, 4]])
A_inv = np.linalg.inv(A) #逆行列の計算
display(A_inv)
np.dot(A, A_inv) #AとAの逆行列の積 ※確認用
[Out]
array([[-2. , 1. ],
[ 1.5, -0.5]])
array([[1.0000000e+00, 0.0000000e+00],
[8.8817842e-16, 1.0000000e+00]])なお後述する対角以外が0の対角行列$${D}$$の逆行列$${D^{-1}}$$はすべての要素が逆数になります。
[IN]
A=np.array([[1, 0, 0, 0],
[0, 2, 0, 0],
[0, 0, 10, 0],
[0, 0, 0, 100]])
np.linalg.inv(A)
[OUT]
array([[1. , 0. , 0. , 0. ],
[0. , 0.5 , 0. , 0. ],
[0. , 0. , 0.1 , 0. ],
[0. , 0. , 0. , 0.01]])$$
\bm D=\begin{pmatrix} a_{11} & 0 & \ldots & 0 \\ 0 & a_{22} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & a_{nn} \end{pmatrix},
\bm D^{-1}=\begin{pmatrix} \frac{1}{a_{11}} & 0 & \ldots & 0 \\ 0 & \frac{1}{a_{22}} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \frac{1}{a_{nn}} \end{pmatrix}
$$
$$
\bm D\cdot\bm D^{-1}=\begin{pmatrix} a_{11}\times\frac{1}{a_{11}} & 0 & \ldots & 0 \\ 0 & a_{22}\times\frac{1}{a_{22}} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & a_{nn}\times\frac{1}{a_{nn}} \end{pmatrix}
=\begin{pmatrix} 1 & 0 & \dot & 0 \\ 0 & 1 & \dot & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dot & 1\end{pmatrix}
$$
[IN]
[OUT]4-3.連立方程式の解法:linalg.solve()
linalg.solve()で連立方程式を解くことが出来ます。大前提として「変数の数≦方程式の数」でないと計算はできません。
参考例として下記問題を解きます。答えは$${x_{1}=-1, x_{2}=1}$$です。
$$
x_{1}+2x_{2}=1\\
3x_{1}+5x_{2}=2
$$
線形代数にすると下記の通りです。
$$
A=\begin{bmatrix} 1 & 2 \\ 3 & 5 \end{bmatrix}, X= \begin{bmatrix} x_{1}\\ x_{2} \end{bmatrix}, Y=\begin{bmatrix} 1\\ 2 \end{bmatrix}とすると
$$
$$
\begin{bmatrix} 1 & 2 \\ 3 & 5 \end{bmatrix} \begin{bmatrix} x_{1}\\ x_{2} \end{bmatrix}=\begin{bmatrix} 1\\ 2 \end{bmatrix}->AX=Y
$$
両辺に逆行列をかけるとXが求まります。
$$
A^{-1}AX=X=A^{-1}Y
$$
これを求めるには①Aの逆行列$${A^{-1}}$$を求めて、②従属変数yに逆行列を内積計算することで求まります。これを一括で処理してくれるのがlinalg.solve()です。
[IN]
a = np.array([[1, 2], [3, 5]])
y = np.array([1, 2])
x = np.linalg.solve(a, y)
x
[OUT]
array([-1., 1.])確認として逆行列を計算して内積を計算しても同じ解となりました。
[IN]
np.linalg.inv(a)@y
[OUT]
array([-1., 1.])4-4.行列式:linalg.det()
追って
5.線形代数2:応用編
5-1.LU分解
LU分解とは行列Aに対して上三角行列Uと下三角行列Lの内積がAになるように分解する処理のことです。
なおNumpyではLU分解用のメソッドがないため別のライブラリとしてscipyを使用します。
5-1ー1.LU分解の特徴
LU分解ができると連立方程式が簡単に解けるため「連立方程式の数値解法として直接法で数値計算(つまり数値シミュレーションができる)」が可能となります。
なおLU分解では分解できない行列があるため適用範囲が広いPLU分解を使用します。Pは置換行列(行列の行や列を入れ替える行列)です。
$$
LU分解:A=LU \\
PLU分解:A=PLU
$$
$$
\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix} =\begin{bmatrix}1&0&0\\l_{21}&1&0\\l_{31}&l_{32}&1\end{bmatrix} \begin{bmatrix}u_{11}&u_{12}&u_{13}\\0&u_{22}&u_{23}\\0&0&u_{33}\end{bmatrix}
$$
5ー1-2.LU分解による連立方程式
LU分解で連立方程式を解いてみます。方程式は$${AX=Y}$$とします。
$$
A=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}, X=\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}, Y=\begin{bmatrix}y_{1}\\y_{2}\\y_{3}\end{bmatrix}
$$
$$
AX=YよりLU分解するとLUX=Y
$$
$$
UX=CとするとLUX=LC ※Cは行列サイズより\begin{bmatrix}c_{1}\\c_{2}\\c_{3}\end{bmatrix}とする
$$
$$
LC=Yより \begin{bmatrix}1&0&0\\l_{21}&1&0\\l_{31}&l_{32}&1\end{bmatrix}\begin{bmatrix}c_{1}\\c_{2}\\c_{3}\end{bmatrix}=\begin{bmatrix}y_{1}\\y_{2}\\y_{3}\end{bmatrix}
$$
上記$${LC=Y}$$より上から計算するとCが求まる。
$$
y_{1}=c_{1} \\
y_{2}=l_{21}c_{1}+c_{2}=l_{21}y_{1}+c_{2}よりc_{2}=y_{2}- l_{21}y\\
y_{3}=l_{31}c_{1}+l_{32}c_{2}+c_{3}=l_{31}y_{1}+l_{32}(y_{2}- l_{21}y)+c_{3}=よりc_{3}=y_{3}-l_{31}y_{1}-l_{32}(y_{2}- l_{21}y)
$$
次に$${UX=C}$$よりXが求まる。
$$
UX=Cより \begin{bmatrix}u_{11}&u_{12}&u_{13}\\0&u_{22}&u_{23}\\0&0&u_{33}\end{bmatrix}\begin{bmatrix}x_{1}\\x_{2}\\x_{3}\end{bmatrix}=\begin{bmatrix}c_{1}\\c_{2}\\c_{3}\end{bmatrix}
$$
上記$${UX=C}$$より下から計算するとXが求まる。
$$
u_{33}x_{3}=c_{3} より x_{3}=\frac{c_{3}}{u_{33}} \\
$$
$$
u_{22}x_{2}+u_{23}x_{3}=c_{2} より x_{2}=\frac{c_{2}-u_{23}x_{3}}{u_{22}}
$$
$$
u_{11}x_{1}+u_{12}x_{2}+u_{13}x_{3}=c_{1}より x_{1}=\frac{c_{1}-u_{12}x_{2}-u_{13}x_{3}}{u_{11}}
$$
5ー1-3.scipyによるLU分解1:lu
ScipyによるLU分解は”scipy.linalg”メソッドを使用します。下記の通り計算はPLU分解であることに注意が必要です。
なおメソッドは①luと②lu_factor(+lu_solove)があり用途に応じて使い分けが必要です。
$$
PLU分解:A=PLU (P=P^TよりPA=LU)
$$
【luメソッド】
luメソッドの特徴は下記の通りです。
※P:置換行列、L:LU分解の下三角行列、U:LU分解の上三角行列
行列Aの置換行列PAに対する(P, L, U)を出力する
出力はLとUは行列Aの置換したものになる(A=LUではなくPA=LU)
出力の全内積をとると元の行列に戻る(A=PLU)
[IN]
from scipy.linalg import lu_factor, lu_solve, lu
A = np.array([[0, 6, 7],
[10, 20, 23],
[15, 50, 67]])
P, L, U = lu(A) #P:置換行列, L:下三角行列, U:上三角行列
print(f'P = {P}', end='\n\n')
print(f'L = {L}', end='\n\n')
print(f'U = {U}', end='\n\n')
print(f'L@U = {L@U}', end='\n\n') #元の行列Aが置換された置換状態
print(f'P@L@U = {P@L@U}', end='\n\n') #元の行列Aに戻る
[OUT]
P = [[0. 0. 1.]
[0. 1. 0.]
[1. 0. 0.]]
L = [[ 1. 0. 0. ]
[ 0.66666667 1. 0. ]
[ 0. -0.45 1. ]]
U = [[ 15. 50. 67. ]
[ 0. -13.33333333 -21.66666667]
[ 0. 0. -2.75 ]]
L@U = [[15. 50. 67.]
[10. 20. 23.]
[ 0. 6. 7.]]
P@L@U = [[ 0. 6. 7.]
[10. 20. 23.]
[15. 50. 67.]]
array([[ 16. , 50. , 67. ],
[ 0.66666667, -12.33333333, -21.66666667],
[ 0. , -0.45 , -1.75 ]])$$
\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix}\begin{pmatrix} 0 & 6 & 7 \\ 10 & 20 & 23 \\ 15 & 50 & 67 \end{pmatrix}=\begin{pmatrix} 15 & 50 & 67 \\ 10 & 20 & 23 \\ 0 & 6 & 7 \end{pmatrix}
$$
$$
PA=LUより \begin{pmatrix} 15 & 50 & 67 \\ 10 & 20 & 23 \\ 0 & 6 & 7 \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\ 0.667 & 1 & 0 \\ 0.333 & 0.8 & 1 \end{pmatrix}\begin{pmatrix} 15 & 50 & 60 \\ 0 & -13.33 & -21.67 \\ 0 & 0 & 2 \end{pmatrix}
$$
$$
A=PLUより \begin{pmatrix} 0 & 6 & 7 \\ 10 & 20 & 23 \\ 15 & 50 & 67 \end{pmatrix}=\begin{pmatrix} 0 & 0 & 1 \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{pmatrix}\begin{pmatrix} 1 & 0 & 0 \\ 0.667 & 1 & 0 \\ 0.333 & 0.8 & 1 \end{pmatrix}\begin{pmatrix} 15 & 50 & 60 \\ 0 & -13.33 & -21.67 \\ 0 & 0 & 2 \end{pmatrix}
$$
5-1-4.scipyによるLU分解2:lu_factor()
【lu_factorメソッド+lu_solve】
luメソッドの特徴は下記の通りです。
出力はluメソッドでも計算したL+Uから対角成分を1引いたものと、置換行列Pを表現するピボットインデックス を返す
lu_solve(<出力のLU>, <従属変数y>)メソッドと合わせて使用することで方程式を計算することができる。
[IN]
LU, piv = lu_factor(A)
LU, piv
[OUT]
array([[ 15. , 50. , 67. ],
[ 0.66666667, -13.33333333, -21.66666667],
[ 0. , -0.45 , -2.75 ]])
array([2, 1, 2], dtype=int32)参考までにluメソッドのLとUから計算すると下記の通りです。
[IN]
L+U-np.eye(3)
[OUT]
array([[ 15. , 50. , 67. ],
[ 0.66666667, -13.33333333, -21.66666667],
[ 0. , -0.45 , -2.75 ]])lu_factor()とlu_solve()を併用して連立方程式を計算してみます。
$$
2x_{1}+5x_{2}=3\\ x_{1}-3x_{2}=2
$$
$$
AX=Yより \begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}\begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}=\begin{pmatrix} y_{1} \\ y_{2} \end{pmatrix}
$$
$$
\begin{pmatrix} 2 & 5 \\ 1 & -3 \end{pmatrix}\begin{pmatrix} x_{1} \\ x_{2} \end{pmatrix}=\begin{pmatrix} 3 \\ 2 \end{pmatrix}
$$
上記より解は$${x_{1}=1.727}$$、$${x_{2}=-0.091}$$となる。
[IN]
import numpy as np
from scipy.linalg import lu_factor, lu_solve, lu
A = np.array([[2, 5],
[1, -3]])
Y = np.array([3, 2]).reshape(-1,1) #列ベクトルに変換
x1, x2 = None, None #解を入れる変数
X = np.array([x1, x2]).reshape(-1,1) #列ベクトルに変換
#LU分解による直接法
LU, piv = lu_factor(A)
X = lu_solve((LU, piv), Y)
print(X)
[OUT]
[[ 1.72727273]
[-0.09090909]]5-2..コレスキー分解:linalg.cholesky
コレスキー分解は対称行列に特化したLU分解であり、対称行列の分解を効率よく行えるものです(コレスキー分解は対象の行列がLU分解が可能な対称行列である場合のみ)。
$$
A=LL^T (L:下三角行列, L^T:Lの転置行列)
$$
[IN]
A = np.array([[2, 1, 1],
[1, 2, 1],
[1, 1, 2]])
L = np.linalg.cholesky(A) # 行列AをQR分解
display(L)
display(L.T)
display(L@L.T)
[OUT]
array([[1.41421356, 0. , 0. ],
[0.70710678, 1.22474487, 0. ],
[0.70710678, 0.40824829, 1.15470054]])
array([[1.41421356, 0.70710678, 0.70710678],
[0. , 1.22474487, 0.40824829],
[0. , 0. , 1.15470054]])
array([[2., 1., 1.],
[1., 2., 1.],
[1., 1., 2.]])$$
\begin{pmatrix} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \end{pmatrix}=\begin{pmatrix} \sqrt{2} & 0 & 0 \\ \frac{\sqrt{2}}{2} & \sqrt{\frac{3}{2}} & 0 \\ \frac{\sqrt{2}}{2} & \sqrt{\frac{1}{6}} & 2\sqrt{\frac{1}{3}} \end{pmatrix}\begin{pmatrix} \sqrt{2}& \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ 0 & \sqrt{\frac{3}{2}} & \sqrt{\frac{1}{6}} \\ 0 & 0 & 2\sqrt{\frac{1}{3}} \end{pmatrix}
$$
6.応用編
6-1.ガウスの消去法(直接法)
ガウスの消去法はLU分解と合わせて連立方程式の数値解法の中で直接法に分類させるアルゴリズムです。直接解けるのであれば計算精度はよく収束しやすいが、結果をメモリに乗せるため大規模な計算には不向きです。
下記記事は非常にわかりやすいため参考にしたうえで、コードは自分が分かりやすいように改造しました。
下記がサンプル問題です。
$$
\left\{\begin{matrix} x_{1}-x_{2}-2x_{3}+2x_{4}=5\\ 2x_{1}-x_{2}-3x_{3}+3x_{4}=10\\ -x_{1}+3x_{2}+3x_{3}-2x_{4}=2\\ x_{1}+2x_{2}-x_{4}=-10 \end{matrix}\right.
$$
6-3-1.前進消去
前進消去法では下図の通り対角成分が1になるように下記を繰り返します。
①i行目のデータに対して対角成分$${a_{ii}}$$を割る
②各行jの要素$${a_{ji}}$$をi行目データにかけてj行目から引くこ

6-3-2.後退代入
前進消去で求めた値から変数Xを求めます。現在の状態は下記の通りです。
$$
\begin{bmatrix} 1& a_{12}& a_{13}& a_{14}\\ 0& 1& a_{23}& a_{24}\\ 0& 0& 1& a_{34}\\ 0& 0& 0& 1 \end{bmatrix} \begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{bmatrix}=\begin{bmatrix} b_{1}\\ b_{2}\\ b_{3}\\ b_{4} \end{bmatrix}
$$
$$
\begin{bmatrix} x_{1}+ a_{12}x_{2}+ a_{13}x_{3}+ a_{14}x_{4}\\ x_{2}+ a_{23}x_{3}+ a_{24}x_{4}\\ x_{3}+ a_{34}x_{4}\\ x_{4} \end{bmatrix} =\begin{bmatrix} b_{1}\\ b_{2}\\ b_{3}\\ b_{4} \end{bmatrix}
$$
数式から下記のことが理解できます。
処理は下の行から計算する(Pythonのループは逆向きに処理)
解$${x_{i}}$$の計算にはそれ以前に計算(下の行にある)した解$${x_{j}}$$を使用する(i<j)。
上記より一番下の行の対角成分$${x_{ii}}$$をとり、そのxの列における各行の要素$${a_{ji}}$$を定数bから引くことで解を求めることが出来る。
Step1:最終行の解$${x_{4}}$$をそのまま求める
$$
\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{bmatrix}=\begin{bmatrix} b_{1}\\ b_{2}\\ b_{3}\\ b_{4} \end{bmatrix}
$$
Step2:$${x_{4}}$$を用いて対角成分の列jにおける成分aを引く($${x_{3}}$$算出)
$$
\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{bmatrix}=\begin{bmatrix} b_{1}-a_{14}x_{4}\\ b_{2}-a_{24}x_{4}\\ b_{3}-a_{34}x_{4}\\ b_{4} \end{bmatrix}
$$
Step3:$${x_{3}}$$を用いて対角成分の列jにおける成分aを引く($${x_{2}}$$算出)
$$
\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{bmatrix}=\begin{bmatrix} b_{1}-a_{14}x_{4}-a_{13}x_{3}\\ b_{2}-a_{24}x_{4}-a_{23}x_{3}\\ b_{3}-a_{34}x_{4}\\ b_{4} \end{bmatrix}
$$
Step4:$${x_{2}}$$を用いて対角成分の列jにおける成分aを引く($${x_{1}}$$算出)
$$
\begin{bmatrix} x_{1}\\ x_{2}\\ x_{3}\\ x_{4} \end{bmatrix}=\begin{bmatrix} b_{1}-a_{14}x_{4}-a_{13}x_{3}-a_{12}x_{2}\\ b_{2}-a_{24}x_{4}-a_{23}x_{3}\\ b_{3}-a_{34}x_{4}\\ b_{4} \end{bmatrix}
$$
6-3-3.コードの実装
前進消去と後退代入の動作が分かるようにメソッドを分けて、かつ出力を保持できるようにクラス化しました。
実際の動作は全項記載の数式どおりです。
[IN]
class GaussianElimination:
def __init__(self, A, Y):
self.A = A #係数行列
self.Y = Y
self.rows = len(Y)
self.X = np.zeros_like(self.Y) #解を入れる変数
def forward_elimination(self):
for row in range(self.rows):
col = row #対角成分の列番号
elem_diagonal = self.A[row, col] #対角成分(Pivot)
self.A[row] = self.A[row]/elem_diagonal #対角成分を1にする
self.Y[row] = self.Y[row]/elem_diagonal #上記に合わせてYも変換
for row_next in range(row+1, self.rows):
elem_p = self.A[row_next, col] #Pivotの下の列要素
self.A[row_next] = self.A[row_next] - elem_p*self.A[row] #Pivotの下の行を変換
self.Y[row_next] = self.Y[row_next] - elem_p*self.Y[row] #上記に合わせてBも変換
return self.A, self.Y
def back_Substitution(self):
for row in reversed(range(self.rows)):
col_X = row #求めたいXの列番号
self.X[row] = self.Y[row]/self.A[row, col_X]
# print(row,'X:', self.X) #途中経過を表示
for row2 in range(row):
self.Y[row2] = self.Y[row2] - self.A[row2, col_X]*self.X[row]
# print(f'Y{row2+1}=Y{row2+1}-A{row2+1}{col_X+1}*X{row+1}={self.Y[row2]}')
def __call__(self):
self.forward_elimination()
self.back_Substitution()
return self.X
A = np.array([
[1, -1, -2, 2],
[2, -1, -3, 3],
[-1, 3, 3, -2],
[1, 2, 0, -1]], dtype=float)
b = np.array([5, 10, 2, -10], dtype=float)
#ガウスの消去法
gaussElim = GaussianElimination(A, b)
gaussElim()
[OUT]
array([ 9., -4., 15., 11.])参考資料
SEGA社が無料公開している「基礎線形代数講座」は具体例や図解が多くてわかりやすい
— 🎍QDくん🎍Python x 機械学習 x 金融工学 (@developer_quant) December 23, 2022
SEGA公式による紹介ページhttps://t.co/xw0Px6qBdm
pdf@GoogleDrivehttps://t.co/exmVd87JIy
ベクトル
内積,外積
行列
連立一次方程式
行列式
線形変換
逆行列
基底の変換
固有値,固有ベクトル
対角化
回転の表現 pic.twitter.com/MJl6REpaCH
あとがき
np.linalgで行列を再勉強しているけど、高校の数学でせっせとやってたことが今となって数値シミュレーションのための基礎学問であることを知った・・・・・・
