続・打者成績を主成分分析したら村上が異次元だった【再分析・クラスタリング編】

こんにちは、いけだです。

前回の記事で、2022年度規定打席到達者の主成分分析を行いました。

前回の分析結果

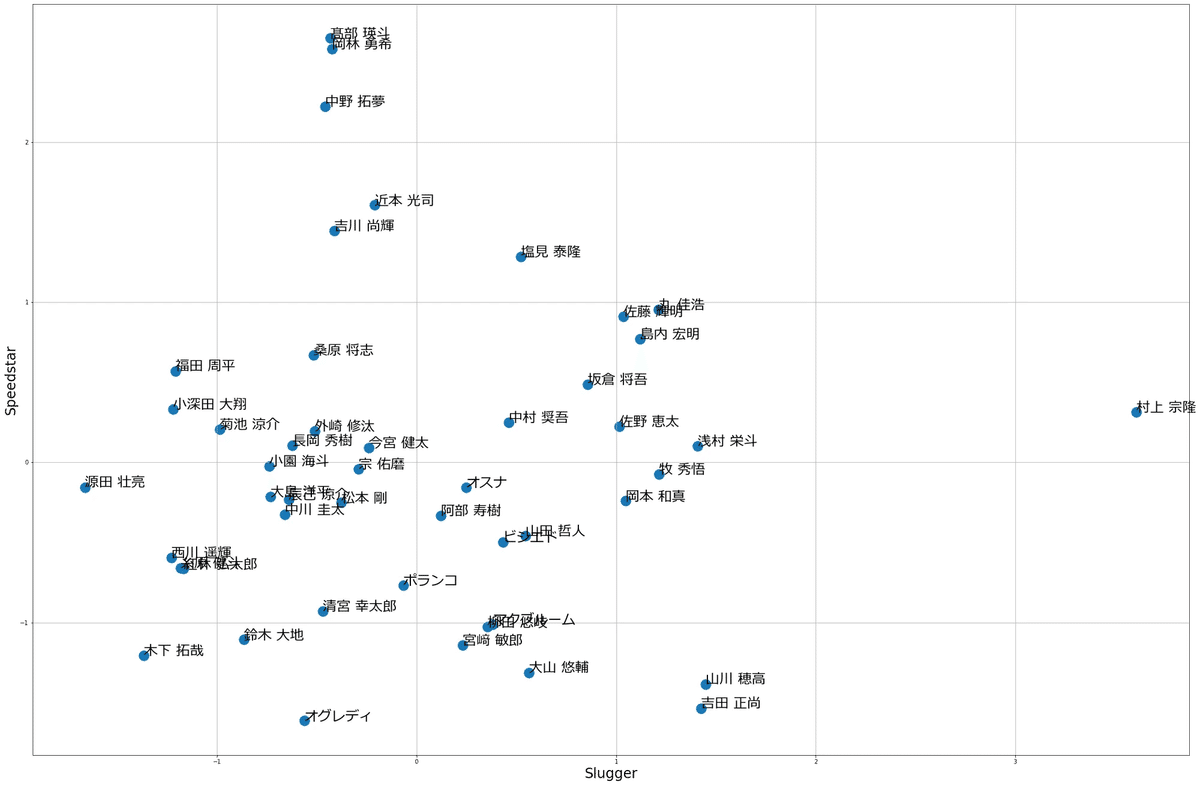
今回は、前回の反省点を踏まえつつ、より分析を深めていきたいと思います。

前回の反省

改善点①指標を割合に統一

前回は、とりあえずすべての項目を分析対象としたのですが、結果として、第2主成分（Speedstarスコア）と最も相関が高い項目が「打数」となっていました。

「打数」という指標は、打順やチーム状況によって数字が大きく変わります。
そのため「打数」は、ほかの選手に比べどのくらいチャンスが与えられたか、ということを測れはしますが、直接的に選手の実力を示すような指標ではありません。
安打数や塁打数など、その他の積み上げ式の指標も多少なりとも同様のことがいえるかと思います。

もちろん、積み上げられた数字は、それだけチームに貢献したという証拠でもあります。
ですが、今回分析対象の選手はすべて規定打席到達者のため、ある意味、今回の分析対象者はチームに一定量の貢献をした選手ばかりです。

そこで今回の分析では、打率（安打数÷打席数）のように、すべての指標を打数や打席数で割り、1打席当たりの期待値で選手を分析していきたいと思います。

改善点②クラスタリング分析を実施

前回の分析では、選手がどのような特徴を持っているか、筆者の主観で判断していました。
今回は、k-means法を利用して、客観的にグループ分けを行います。

k-means法とは、データを複数グループに分ける（クラスタリングする）方法です。注意点として、クラスタ数を事前に設定する必要があります。
今回は適切なクラスタ数も併せて計算していきます。

クラスタリングのイメージは下記サイトが分かりやすかったので、ご参考にどうぞ。
（参考）【入門】k-means法とは？可視化してわかりやすく解説 - ほげほげテクノロジー 

Pythonによる主成分分析

CSVの読み込み

今回もデータ元は プロ野球データFreak様 です。
（引用データ元ページは こちら）

import pandas as pd
df = pd.read_csv('npb_batting_2022.csv')

累積指標を割合に変換

ここからは累積型の指標を割合に変換していきます。
基本的には累積指標を打数で割りますが、四球や犠打など、記録上打数カウントされないものは打席数で割っていきます。

#累積型指標の割合化
df['二塁打率'] = df['二塁打'] / df['打数']
df['三塁打率'] = df['三塁打'] / df['打数']
df['本塁打率'] = df['本塁打'] / df['打数'] #既存指標の本塁打率とは違います　
df['打点率'] = df['打点'] / df['打数']
df['盗塁率'] = df['盗塁'] / df['打数']
df['盗塁刺率'] = df['盗塁刺'] / df['打数']
df['犠打率'] = df['犠打'] / df['打席数']
df['犠飛率'] = df['犠飛'] / df['打席数']
df['四球率'] = df['四球'] / df['打席数']
df['敬遠率'] = df['敬遠'] / df['打席数']
df['死球率'] = df['死球'] / df['打席数']
df['三振率'] = df['三振'] / df['打数']
df['併殺打率'] = df['併殺打'] / df['打数']

#必要なデータのみを抜き出す
df2 = df[['選手名', 'チーム', '打率','出塁率', '長打率', '二塁打率', '三塁打率',
          '本塁打率','打点率', '盗塁率', '盗塁刺率','犠打率', '犠飛率',
          '四球率', '敬遠率', '死球率', '三振率', '併殺打率']]

データの標準化とモデル作成・学習

データの標準化から主成分の作成とデータフレーム化まで行います。

#データの標準化
df3 = df2.loc[:,'打率':].astype('float')
sc = StandardScaler()
sc_df = sc.fit_transform(df3)

from sklearn.decomposition import PCA

#モデル作成
model = PCA(n_components=2, whiten=True)
#モデル学習
model.fit(sc_df)

#作成した主成分でデータフレーム作成
new = model.transform(sc_df)
new_df = pd.DataFrame(new)
new_df.columns=['PC1','PC2'] #主成分に仮命名
new_df.head(5)

[実行結果]
-----------
	PC1	PC2
0	0.954225	-0.125084
1	0.538910	-0.167895
2	3.042406	3.229608
3	-1.427309	0.396093
4	-1.428882	1.259926

生成された主成分と既存項目との相関性を確認

まずはPC1について、相関性の高い項目を確認します。

#標準化データと生成された2軸を合体
df4 = pd.DataFrame(sc_df,columns=df3.columns)
df5 = pd.concat([df4,new_df],axis=1)

#打率～長打率とPC1の相関性を確認
df_corr = df5.corr()
pc_corr = df_corr.loc[:'併殺打率','PC1':]
pc_corr['PC1'].sort_values(ascending=False)

[実行結果]
-----------
打点率     0.939057
長打率     0.908197
本塁打率    0.888629
敬遠率     0.801036
四球率     0.764644
出塁率     0.716967
　　　（中略）
三塁打率   -0.528810
犠打率    -0.715634

第1主成分（PC1）と相関性が高い項目として、打点、長打、本塁打、敬遠などがあるようです。また、負の相関として犠打（バント）もあります。

pc_corr['PC2'].sort_values(ascending=False)

[実行結果]
-----------
盗塁率     0.743336
盗塁刺率    0.698795
出塁率     0.527193
打率      0.422989
三塁打率    0.392797
　　　（中略）
犠飛率    -0.392798
併殺打率   -0.473699

同様に、第2主成分（PC2）は盗塁や出塁率と相関が高いようです。

ここからは名づけのセンスが問われるのですが、私は今回、主成分の要素を見比べたときに、第1主成分が松井秀喜選手、第2主成分がイチロー選手っぽいなと（なんとなく）直感的に思ったため、それぞれをMatsuiスコア、Ichiroスコアと名付けてみます。

#PCの名前変更
col = ['Matsui','Ichiro']
new_df.columns = col

これで主成分の確認は完了です。

クラスタリング

次に、第1,第2主成分で作られる散布図について、クラスタリングをしていきます。

クラスタ数の決定

今回、クラスタ数の確認にはエルボー法を用います。
エルボー法とは、クラスタ数を変えながらSSE(*1)と呼ばれる数値を計算し、出てきたSSEをグラフ化することで、最適（だと思われる）クラスタ数を推定する手法です。

今回はクラスタ数2~16の範囲でSSE計算を実行してみます。

from sklearn.cluster import KMeans
sse_list = []
for n in range(2,16):
    model = KMeans(n_clusters=n, random_state=0)
    model.fit(new_df)
    sse = model.inertia_ #SSEの計算
    sse_list.append(sse)

sse_list

[実行結果]
-----------
sse_list
[54.05679878401011,
 31.214412207302267,
 20.620078554732984,
 14.940115386928413,
 11.22572990069186,
　　（略）

SSEの計算ができたので、これを図示してみます。

se = pd.Series(sse_list)
num = range(2,16)
se.index = num
se.plot(kind = 'line', marker = 'o')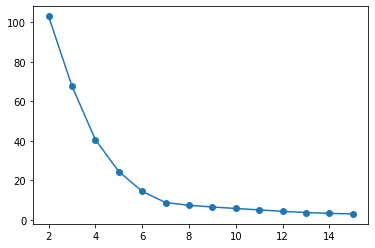

x軸はクラスタ数、y軸はSSE値

エルボー法では、グラフを人の腕に見立て、肘の部分（SSE値の減少が緩やかになる点）を見つけます。
そして、その肘となるクラスタ数こそが、最適なクラスタ数だと言われています。
グラフを見るに、今回は5~7あたりに肘がありそうです。
中間の「6」を最適なクラスタ数とみなしましょう。

データのクラスタリングと整形

最適なクラスタ数が把握できたので、いよいよデータをクラスタリングしていきます。

#クラスタリング
model = KMeans(n_clusters=6, random_state=0)
model.fit(new_df)

#主成分データにクラスタ番号追加
new_df['Cluster'] = model.labels_

#主成分データに選手名を追加
df_name = df[['選手名','チーム']]
df6 = pd.concat([df_name,new_df],axis=1)

df6.head(5)

[実行結果]
-----------
	選手名	チーム	Matsui	Ichiro	Cluster
0	浅村 栄斗	楽天	0.954225	-0.125084	0
1	島内 宏明	楽天	0.538910	-0.167895	0
2	村上 宗隆	ヤクルト	3.042406	3.229608	3
3	中野 拓夢	阪神	-1.427309	0.396093	2
4	岡林 勇希	中日	-1.428882	1.259926	2

クラスタリングを実施したうえで、
選手名、主成分、クラスタ番号が1つにまとまりました。

散布図でプロット

最後に、散布図をプロットします。

#色を定義
colors = ['red','blue','yellow','cyan','green','black']
cmap = ListedColormap(colors)

df6['Cluster'] = df6['Cluster'].astype(int)

#軸設定
import matplotlib.pyplot as plt
x = df6['Matsui']
y = df6['Ichiro']
labels = df6['選手名'] #データラベル用

#プロットの詳細設定
plt.figure(figsize=(36,24))
plt.xlabel('Matsui', fontsize=24)
plt.ylabel('Ichiro', fontsize=24)
plt.scatter(x, y, s=300,c=df6['Cluster'],cmap=cmap)
for i, label in enumerate(labels):
    plt.text(x[i], y[i], label, fontname="Meiryo", fontsize=24)
plt.grid(True)
plt.show()

以上でプロット完了です。

分析結果

やはり村上選手はすごかった

分析結果は以下の通りです。

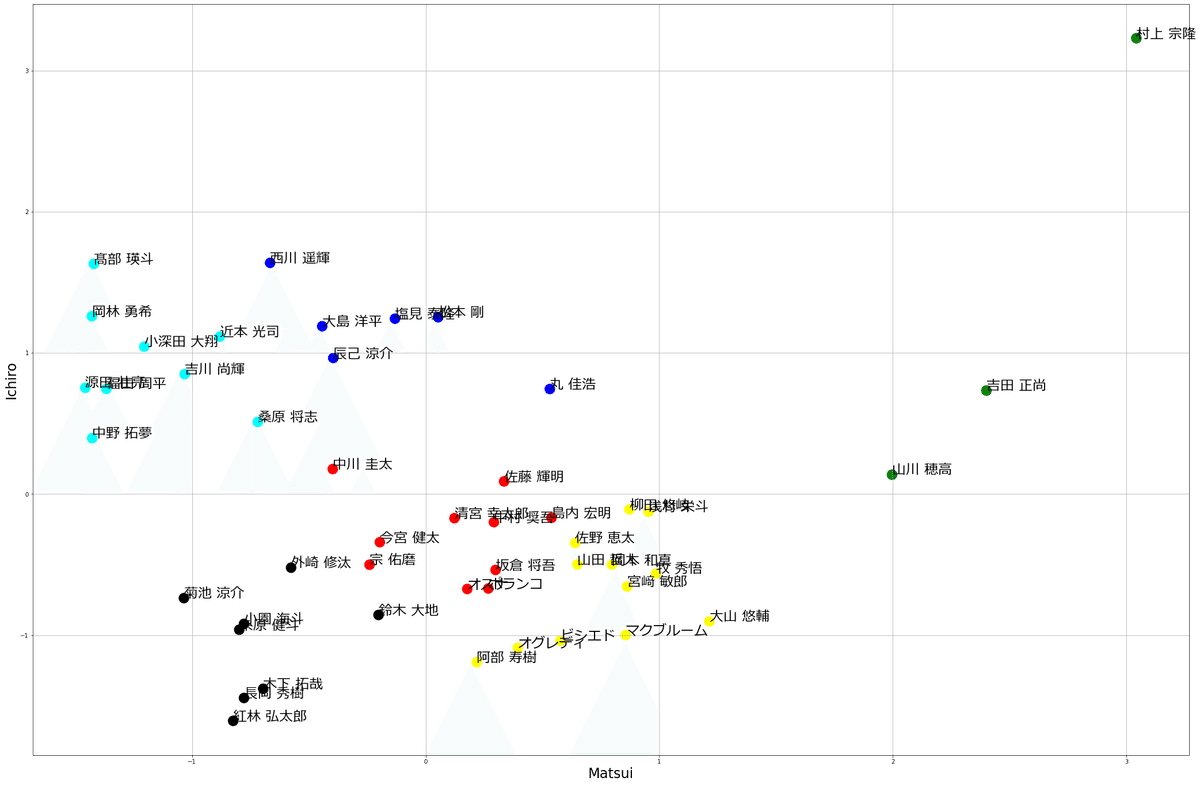
や、やっぱり村上異次元すぎる～～～～～！！！

1打席当たりの期待値ベースで考えても、村上選手の異次元さは変わりませんでした。
むしろ、より際立ったと言えます。
Matsuiスコア、Ichiroスコアともに3越えですが、その他の選手でスコアが3に到達した選手は、単独スコアでもいませんでした。
改めて村上選手のすごさが浮き彫りになりましたね。

また、村上選手ほどではありませんが、山川選手や吉田選手も、他選手と一つ違った立ち位置にいるようです。
（実際に、後述のクラスタリングでは村上選手と同クラスタにいます）

クラスタごとに見る

ここからは、クラスタごとに選手を見ていきます。
クラスタの命名については、所属選手を見ながら適当な名前を付けてみました。
あなたご自身の選手イメージと比べながら、ご覧頂ければと思います。

①規格外

抜きん出た成績の選手が3人おり、彼らで1クラスタ出来ていました。
村上選手の突出具合は言うまでもないのですが、山川選手、吉田選手もMatsuiスコアにおいて、顕著な立ち位置にいます。
実際に、得点との相関関係が高いといわれるOPSでも0.900越えはこの3人のみです。
投手の活躍が目立った今年度において、彼らは特別枠と見たほうがいいかもしれません。

②スピードスター

Ichiroスコアが高く、Matsuiスコアが低い選手が属するクラスタが「スピードスター」です。
身体能力が高く、俊足の選手が存在しています。
「スピードスター」クラスタの選手は、各球団1人は欲しい選手といえるのではないでしょうか。

③アベレージヒッター

「スピードスター」クラスタに長打力を足した選手が属するクラスタが
「アベレージヒッター」です。
個人的に、打率.218の楽天西川選手を「アベレージヒッター」所属にするのは少し違和感がありますが(*2)、とりあえずクラスタ名は「アベレージヒッター」としました。
チームの主力となる選手が多く属していますね。
「スピードスター」に属する選手が次に目指すタイプはこの「アベレージヒッター」クラスタではないでしょうか。

④スラッガー

Matsuiスコアが高く、Ichiroスコアが低い選手が属するクラスタが「スラッガー」です。
パンチ力があり、長打を期待できる選手が多く属しています。
こちらも「アベレージヒッター」クラスタと同じく、チームの中核を担う打者が多く属しています。

⑤バランス型

Matsuiスコア、Ichiroスコアともに全選手の平均に属する選手のクラスタが「バランス型」です。
個人的には、清宮選手が全選手の平均（座標（0,0））に近いのは意外でした。

⑥守備型

Matsuiスコア、Ichiroスコアともに低い値をとる選手が属するクラスタが「守備型」です。
前提として、このクラスタに属する＝守備力が高い、と直接イコールでは結べません。ですが、長打力や出塁力、走力などが相対的に低いにもかかわらず規定打席に到達していることから、打撃や走塁以外の部分（＝守備力）を買われていると推測できます。
実際にここに属する選手はUZRなどの守備評価が高いため、クラスタ名を「守備型」としました。

最後に

いかがでしたか。
1打席ごとの期待値で分析したり、クラスタリングを用いたりすることで、前回よりもより納得感のある分析が行えたのではないでしょうか。

まだまだ浅学の身ではありますが、自分が勉強したことを活かして多少なりとも面白いアウトプットができたと感じたため、記事にしてみました。

今回の分析はあくまで2022年の結果に対する分析でしかなく、「今年はこうだったよねー」といった意味合いが強いです。
例えば「第二の村上選手を生み出すには」「この特徴を持つ選手はこの力を高めると活躍する」といったテーマまで踏み込めると、分析の価値はより高まるかと思います。
今後はそういった分析もできればと思っています。

ここまでご覧いただきありがとうございました。
それでは、さようなら。

(*1)
SSEとは、クラスタ内誤差平方和と呼ばれ、「［クラスタの中心点］と［そのクラスタに所属する点］の距離の2乗」の値を合計したものです。
SSEが小さいほど上手にクラスタリングできていると言えますが、一方でクラスタ数がむやみに増えてしまうのも分析の本質から外れるため、SSEとクラスタ数のちょうどよいバランスを見ていく必要があります（＝エルボー法）

(*2)
楽天西川選手は、打率は低いものの出塁率や盗塁数は多く、Ichiroスコアで高得点となっています。打率など普段よく目にする指標以外で分析すると、こういった新たな発見があってよいですね。