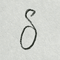高校数学との出会い方
6回目の投稿
みなさまこんにちは(こんばんは)。春本番となりました。今回は中学3年生(新高1)がこの春に出会うもの、「高校数学」についての考えを軽く述べていきたいと思います。
高校数学の世界へLet us go!
さて、中学校を卒業して高校に進学する方が避けられないのが高校数学との出会いです(他の教科も避けられない)。
高校数学と聞いて中学生は何を思い浮かべるか。おそらく、長い数式やsin,cos,tan,cosec,sec,cotなどの記号、Σやδなどの記号でしょう。当然ですが、中学生(数学オタクや公文勢は除く)に意味は分かりません。これが高校数学を難しそうなイメージにしている一番の原因です。
1か月前。いつもの教室での5時間目、春の訪れを感じさせるような暖かな陽気につつまれながら眠い目をこすって解いていたのは三平方の定理。今となっては淡い思い出ですね。
三平方の定理はa^2+b^2=c^2で表されるもので、「なんちゃって余弦定理」です。証明方法がたくさんあり、平面図形や立体図形の問題で多く使われるなど結構ぼりゅーみーです。私の中学時代の先生は数学オタクでしたので証明方法をたくさん教えてくれました。
さて、三平方の定理は「なんちゃって余弦定理」だと先ほど言いました。「余弦定理」って何だ、と思うでしょう。中学生は「余弦定理」と聞くと難しく感じると思います。まぁ、中学校で学ぶ数学に比べたら簡単ではありません。ただ難しくもないです。
マジカルバナナをしよう
マジカルバナナ、バナナと言ったら黄色、黄色と言ったら黄リン、黄リンと言ったらP、Pといったら動点P、動点Pと言ったら図形、図形と言ったら三角形、三角形と言ったら三平方の定理、、、、、、
さて、ここまでマジカルバナナをボッチでやってみましたが、この三平方の定理の次に「余弦定理」という名前のものをいれてみましょう。
三平方の定理と言ったら「よげんていり」、、、、、、
さて、ここまで来たとします。
「よげんていり」とは
高校数学では三角形の角の大きさと辺の長さの関係について考えていきます。三平方の定理は「『直角』三角形」における斜辺の長さを他の2つの辺の長さを利用して表した式ですよね。これを高校数学では「『直角』三角形」を「三角形」に変えて考えるようになるのです。
ここで問題になるのは角度の扱い方です。中学生までは「直角(=90°)」のみで考えてきたので、角度が90度の時のことだけを考えていればよい、という状況だったのです。ただ、これからは違う。角度が30°の時もあれば72°の時だってある、129.99999999°の時だってある。これを1°の時はこうで、2°の時はこうで、、、と覚えていくのは難しいです(というか困難です。数は無限にあるのでその都度覚えていったら∞年かかります)。
じゃあ、なんか角度と辺の長さに法則はないかな、なんか公式にできないかな、という手段を考えざるを得なくなってしまいました。そうして、ある天才は「法則(定理)」を作り出したのです。その名は「余弦定理(よげんていり)」。
私たち学生のノルマは「理解する」ことではなく、「イメージをつかむ」こと
さて、「よげんていり(余弦定理)」が何に使われているか、どんなイメージなのか、なんとなく分かってきたでしょうか。そのイメージがつかめていれば勝ちです。
東大生の高校時代の学習方法でよく出てくるのが、予習です。私は予習をすることの意義をこれから学ぶことについての「イメージを持つこと」だと考えています。内容をしかりと理解するのではなく、イメージをつかむのです(理解できることに越したことなないでしょうが。)。
これからこんな感じのものを学んでいくんだな、というざっくりとしたイメージがあるかないかでは大きな差が出るでしょう。旅行における「下調べ」と同じです(しない方が楽しい、という人もいるが)。何がどんな感じで見られるのかを知っているから、観光を計画通りに効率的に楽しむことができる。これと同じです。何をどんな感じで学ぶのか知っているから、学習を計画通りに効率的に進めることができるのです。
(補足)
筆者は旅はノープランの方が好きです。計画していないから「あっ」と感じる機会が多いのではないでしょうか。でも、このような旅は失敗すると何の思い出にもならないただの移動時間になってしまいます。これが旅であったら何度でも行けますので問題ないですが、勉強となると失敗はできません。ですので、勉強面では予習(下調べ)を行うことが必要だと考えます。
もう一つ。「前提条件」に問いを持つ
さて、私たち学生がやるべきことはもう一つあると私は考えています。これは数学の勉強だけに限ったことではありませんが、前提条件(常識や固定概念、ともいえる)に疑問を持つことです。
私は先ほどこのような文章を書きました。「高校数学では三角形の角の大きさと辺の長さの関係について考えていきます。」と。
なぜ三角形の中で「角」と「辺の長さ」の2つなのか。このような疑問を持ってみましょう。この問いの答えは簡単です。三角形の辺の長さはその辺の向かいにある角度の大きさによって決まっているからです。しかし、
「なんでわざわざ「辺」と「角度」なんだろう」という問い自体を作ることはできますでしょうか。これは難しいです。理由として
1.数学が得意だから
=辺の長さは対角の大きさで決まるからねぇ、というのを知っているから
2.「辺と角度について学ぶ」という前提をそのまま飲み込んでいるから
=先生がそういったのだから、そうなんだ。と考えてしまう。
この2つの理由が考えられます(他にもあるかもしれないです)。1は別にいいでしょう。しかし、2の場合は問題です。先生が言ったことをそのまま「前提」としてそのまま飲み込むことで、「辺と角度について学ぶ」という勉強は受動的なものになってしまいます。勉強は能動的にやった方が効率がいいです。
勉強の効率を上げる。そのためには能動的であることが必要。能動的になるためには、自ら問いをつくることが必要です。
では、問いをつくるためにはどうすればよいか。私自身もよくわかりませんが、少し考えているのは「ひねくれもの」になることです。すべてを懐疑的・批判的に見る、ひねくれた態度で見つめることで、「これおかしいだろ、おい。」という部分(問い)が見つかってくるような気がします。
例えば、先生にしたの2つの公式を教わったとしましょう。
a³+b³=(a+b)³ー3ab(a+b)
a³+b³=(a+b)(a²-ab+b²)
おい、数学教師。なぜ同じ式を2通りの方法で表す必要があるのだ。
というようにひねくれ者になってみて問いを立てればうまくできそうな気がします。
数学の教科書の目次やカリキュラムを見て、なんでこの順なんだろう、という問いもいいでしょう。なんで「三角形の」辺と比について、なんだろう、なんであの数学オタクは「素数は美しい」とぼやいているのだろう。
色々出てきますね。これらの問いを解決することこそが「能動的な学習」であり、思考力を育ててくれると私は思います。
結論
・予習をして「イメージだけでも」掴んでおけば、勉強効率向上
・ひねくれものになって数学の教育や先生、日常に疑問を持ち、それらを解決すると思考力向上・勉強効率向上。
春。別れの季節。そして、「出会いの季節」。
さて、ここまで読んでくださった方が10人いればうれしいものです。
春は「別れの季節」ですね。私も片思いの人とお別れしましたし、651系ともお別れしました。

しかし、時が流れるのは早いもので、出会いの時期にもなってきました。新しい学校、教師との出会い、E257系特急草津・四万との出あい、、、
と色々な出会いがあるかと思います。そして、我々中学生はあるものと出会います。「高校数学」。望まない出会いであると感じる方も多いでしょう。
たしかに出会ってもうれしくないですよね。ただ、数学オタクは違うんです(知らんけど)。数式は数の羅列ではなく、整合性を併せ持った美しい言葉として見えているのです(知らんけど)。
数式の意味が分かるようになり、数式を言葉として使いこなせるようになれば、きっと数学が面白くなっていくのでしょう。これからも頑張っていきましょう。
では、またいつか。