
タレスは何をした?
0.序
(2021年10月11日改訂)
タレスの証言・断片の引用は次の書籍です.
『ソクラテス以前哲学者断片集』岩波書店(2008年)
七賢人の一人として数えられる最初の哲学者タレスには「万物の元のものは水である」という学説の他に様々な業績が残されています.それらは全てタレスのものとして信用できるのでしょうか? 検討してみましょう.
すでに古代において,ディカイアルコス(アリストテレスの弟子)は「彼ら(七賢人)は,哲学者ではなく,頭が良く立法の才能があっただけ」とも言っています.古代においてさせタレスの伝承には疑義があったということになりますね.
まずタレスの年代ですが
アポロドロス『年代記』によれば,タレスが生まれたのは第35(39?)回オリュンピア祭期の最初の年[前640年]であると言っている.そして,78歳で没した(あるいは,ソシクラテスによれば,90歳で没した).彼が没したのは,第58回オリュンピア祭期[前548―545年]のことだったからである.
古代の暦(オリュンピア祭典期)について知りたい方はこちらをどうぞ↓
つまりタレスは前7世紀から前6世紀の人物ということになりますね.ホメロスやヘシオドスよりも後,アイスキュロスやヘロドトスよりも前の人物です.
1. 業績一覧
業績を列挙します.
・『航海用天文詩』を書いたのはタレスではなく,サモスのポコスである.
・カリマコスによれば,こぐま座を発見した.
・ある人たちによれば『太陽の回帰について』と『春分・秋分について』を著した
・ある人たちによれば,太陽の蝕を予言した.
・幾人の人がいうには「魂は不死である」とした.
・ある人たちよれば,太陽の視直径が天球の1/720であると主張した.
・各月の最後の日を「30日(triakas)」と最初にいった.
・アリストテレスによれば,磁石や琥珀によって無生物も魂をもっていると主張した.
・パンピレによれば,はじめて直角三角形を円に内接させて描くことを成し遂げた.
・ロドスのヒエロニュモスによれば,オリーヴの豊作が見込まれそうなときに,それを予知して多数のオリーヴ搾り機を賃借して富みをえたとされる.
・四季の発見と一年を365日に分けたのは彼である.
・ヒエロニュモスによれば,タレスは,われわれの影がわれわれと等身大になるときを見計らって,影を手がかりにピラミッドを測定した.
・星を観察しようと老婆に伴われて家をでたが,穴に落ちて大声をあげた.
・クロイソス王から依頼されて,橋をかけずにハリュス川を渡るために,川の流れを2つに分ける工事を指揮した.
以上が,ディオゲネス・ラエルティオス『哲学者列伝』に記載されている彼の業績です.
2.点検
タレスの業績の真贋については,
ジェフリー・スティーヴン カーク/マルコム スコフィールド /ジョン・アール レイヴン
『ソクラテス以前の哲学者たち』京都大学学術出版会(2006年)
で詳しく検討されています. この本を頼りにタレスの業績について検討してみましょう.
・『航海用天文詩』を書いたのはタレスではなく,サモスのポコスである.
まず,サモスのポコス(フォコス)の著作が,古代において,すでにタレスの名で伝わっていたことが分かります.
・カリマコスによれば,こぐま座を発見した.
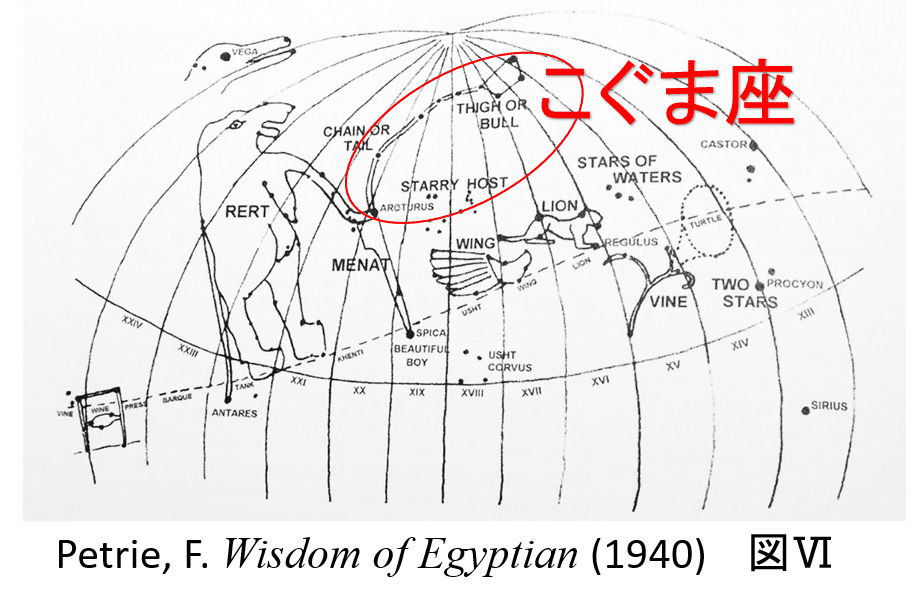
ホメロスとヘシオドスには「こぐま座」への言及はなく,これを否定する根拠はありません.一方で前4世紀以降は,一般的な星座としてこぐま座は普及しています.古代エジプトでは,前2000年頃,こぐま座は「鎖(もしくは,鷹の頭をもつ人間)」として星図に描かれていたと考えられています. ヘシオドスやホメロスにみられないエジプトの星座が,ギリシャに伝承したのが前6世紀である可能性は否定できないため,ギリシャ人としての「こぐま座」の発見(命名)は消去法でタレスとして良いのかもしれません.
・ある人たちによれば『太陽の回帰について』と『春分・秋分について』を著した
太陽年と春分・秋分点の時刻を精密に扱う試みは前5世紀に始まったため前6世紀のタレスにそのような著作があったとは考えらません.ヘシオドスの時代には春分と秋分の日はすでに知られており,タレスが太陽の回帰と春分・秋分の「何」について研究したというのでしょうか?
・ある人たちによれば,太陽の蝕を予言した.
ある地点での日食の予報には,暦の計算に加えて「太陽と月までの相当に正確な距離」が分からなければなりません(※古代はもとより近代に至るまで日食予報を100%的中させることはできませんでした).
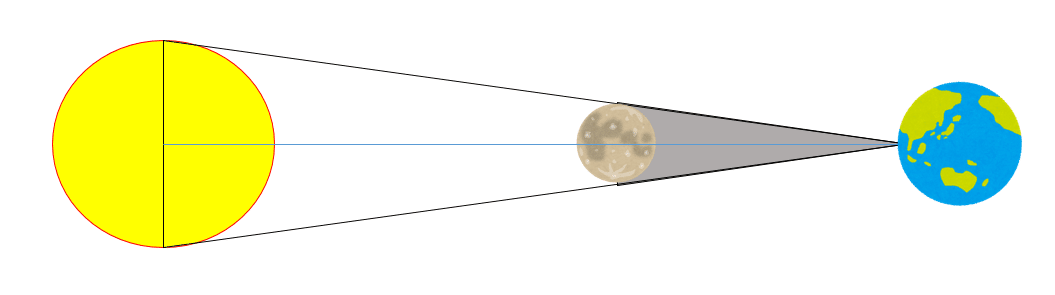
前4世紀のバビロニア(世界最先端の天文学)での日食予報でさえ「日食が起こらないこと」を予報するのが精一杯でした.タレスが日食の予報を,自身で行ったとするのは作り話とする方が適切です.「タレスはバビロニアの天文学の知識を用いて日食を予報した」という記述は,注意の必要な記述です.タレスの時代のバビロニア天文学では,日食予報は不可能なのですから.
なお,タレスの日食予報に関して,近年いくつかの論文が発表されていますが,どれも決定的ではないように思います.ある論文(タレスの日食予報関連)の著者に対して論文の内容を質問したところ,幸いにもお返事をいただけたのですが,加えて不備(致命的な欠陥だと思うのですが)を指摘したところ,残念ながらお返事はありませんでした. タレス以後のギリシャでは暫く日食予報が行われていないことから,偶然の産物であると考えるのが誠実です.少なくとも科学的な予報ではないでしょう.
・ある人たちよれば,太陽の視直径が天球の1/720であると主張した.
これを発見したのはアルキメデスによれば,サモスのアリスタルコスであるとされています.確実に作り話と考えてよいでしょう.
・各月の最後の日を「30日(triakas)」と最初にいった.
これはタレス以前のヘシオドス『仕事と日』766に用例があるため信用できません.
・四季の発見と一年を365日に分けたのは彼である.
四季の発見が何を指すのか不明です.ギリシャ人で四季の長さを測ることを始めたのは,現存する史料ではメトン(前5世紀後半)です.1年を365日に分けていたのはエジプトの暦ですが,アテナイの評議会暦では1年は366日でした.「エジプトでは1年は365日である」と紹介した程度のことはあるかもしれません.エジプトの暦はひと月を30日とし,閏日を5日加える仕組みだったのですが,その意味で月の最後の日を「30日」としたのであれば整合性はとれますが,1年365日の暦がギリシャの都市国家で利用された証拠を知りません.
・星を観察しようと老婆に伴われて家をでたが,穴に落ちて大声をあげた.
同様の話が,プラトン『テアイテトス』174Aにあります.前5世紀頃には,タレスは天文学に通じた人として有名になっていたのでしょう.近年,この逸話についての魅力的な解釈が提示されました.タレスは「落ちた」のではなく「潜った」というものです.遠くを見る際に目を細めたり,ラップフィルムの芯から覗くと,良く見えたという経験はないでしょうか?

望遠鏡以前の天文学では「観測井戸」に入ることで,視野を狭める方法が知られていました.
アリストテレス『動物の発生について』780b20-(今井正浩 訳)
手をかざしたり管を通したりしてものを見ると,色の差異を見分けるのには良くも悪くもならないが,より遠くまで見られる.そこである人たちはときに,穴や井戸の中から天体を見たりする.

つまり,タレスは星を見るために井戸に潜ったのですが,それを理解できない老婆には井戸に落ちたようにみえたのでしょう.しかし,これ以上のことは分からず,タレスが井戸の中から何を観測したのかは不明です.
・天文学によるオリーブの豊作予報 これって現代科学でも予測困難ではないでしょうか?

3.数学
それでは最後に「数学」の業績を点検します.
・ヒエロニュモスによれば,タレスは,われわれの影がわれわれと等身大になるときを見計らって,影を手がかりにピラミッドを測定した.
・パンピレによれば,はじめて直角三角形を円に内接させて描くことを成し遂げた.
他にも次のような業績が挙げられています.
・円が直径によって二等分されることを最初に証明したのはタレス.
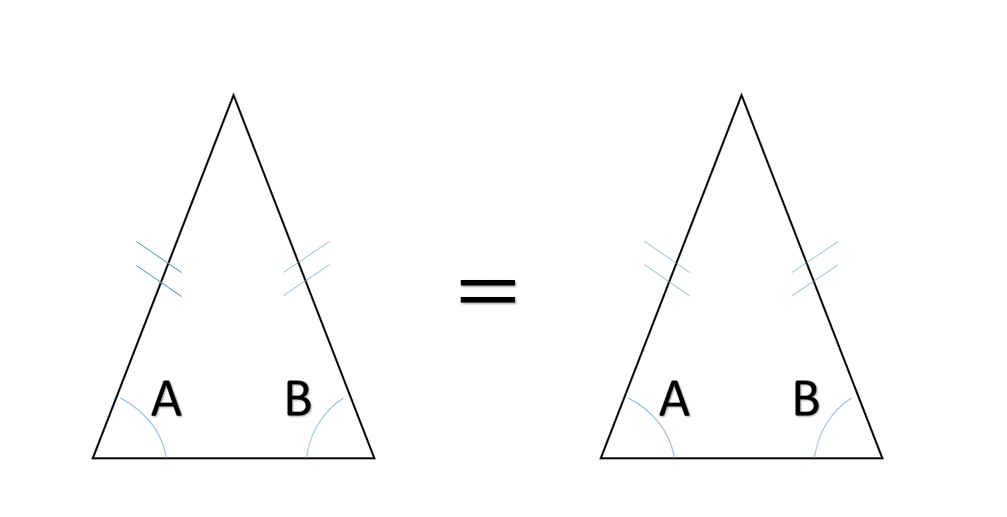
・二等辺三角形の底角は等しいことを証明したのはタレス
・直線が交わったとき二つの対頂角が等しいという定理を証明したのはタレス
・一辺とその両端の角が等しいとき,二つの三角形は合同であるというのを証明したのはタレス,なぜならば,海上の船同士の距離を示すのに用いたと言われている方法にはこの定理を使わなければならないから.
ここで問題となるのは,すべて「証明」を行ったとされていることです.三平方の定理は,ユークリッド『原論』第1巻47 で証明されていますが,ユークリッドの何百年(あるいは何千年?)以上前に,エジプトやメソポタミアでは用いられていました.つまり数学の定理は証明なしでも利用可能なのです.そして,証明を伴う数学,つまり論証数学は前5世紀中頃(前450年頃)に成立したと考えられています.するとタレスは,証明をしていないが,上記の定理が真であることを見抜いたと考えることもできるのですが,
この想定も無理があることは定理を図にすれば一目瞭然です.

円が直径によって二等分されることを発見したことは偉大でしょうか?証明しろといわれると,少し身構えてしまいますが. なお,これは『原論』第1巻定義17です.次に二等辺三角形の底角が等しい.『原論』第1巻命題5ですが,これも見ればわかるでしょ?
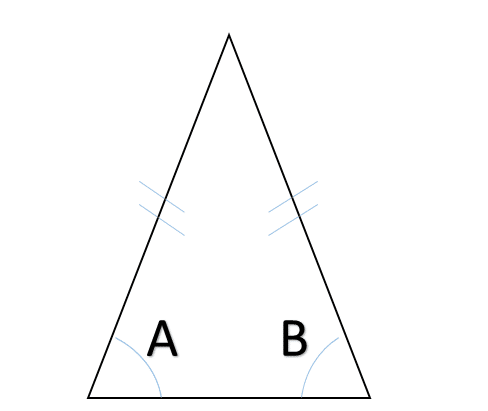
次に対頂角は等しい(つまり∡A=∡B),ですが,これは『原論』第1巻命題15ですね.「俺は証明なしでこれを発見した!」なんて言ってる人っておめでたいでしょ?
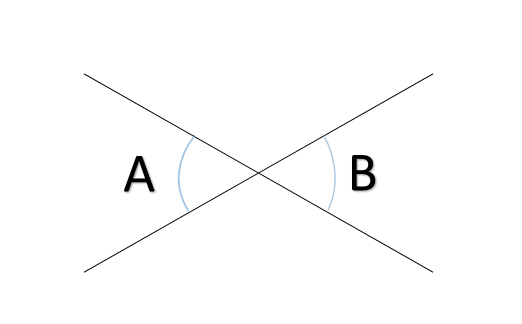
次に,一辺とその両端の角が等しいとき,二つの三角形は合同というのも,『原論』第1巻命題5で証明されており,議論は多少複雑です.でも見ればわかります.
次に,直角三角形を円に内接させて描くことを成し遂げた,これは『原論』第3巻31です.円の直径を斜辺として三角形を作図すれば,それが直角三角形になるのは明白です.

このように,タレスの業績とされる数学上の定理は,すべて「見ればわかる」ものです.そういったことに「証明」が必要だと感じたギリシャ人は偉大なのですが,それは前5世紀になってからです.タレスは証明を知りませんでした.残るはピラミッドの高さの測定です.
ヒエロニュモスによれば,タレスは,われわれの影がわれわれと等身大になるときを見計らって,影を手がかりにピラミッドを測定した.

三角比を用いた測量の起源とされていますが,このような基本的な技術もエジプトでは失われていたのでしょうか? この太陽と三角比を用いて高さを測る方法は,ユークリッド『オプティカ(光学)』命題18です.
太陽が現れているとき,与えられた高さがどれほどであるかを知ること(高橋憲一訳).
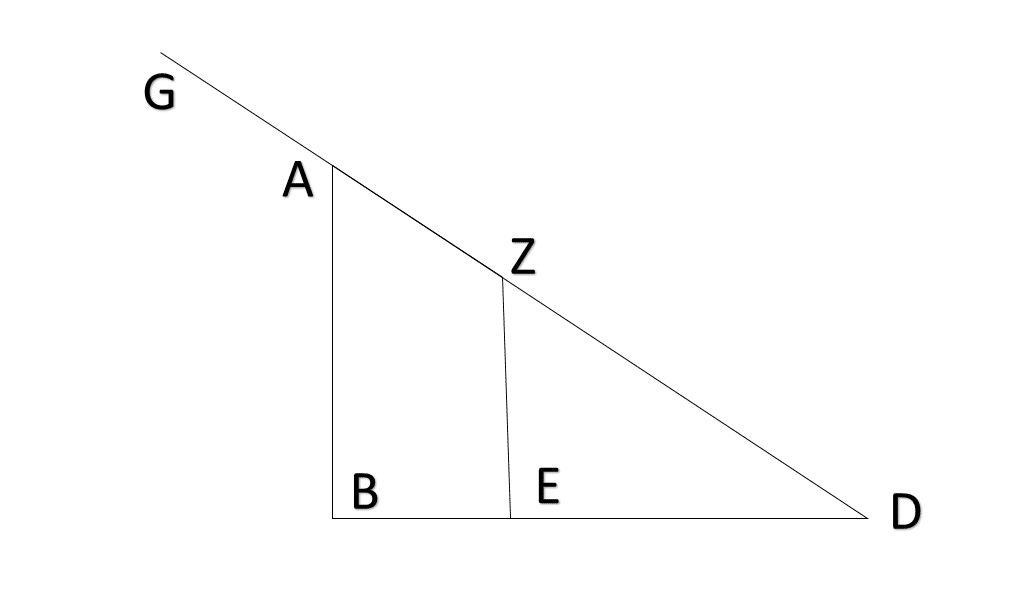
この命題をタレスが証明したという伝承はありません.やはり作り話であろうと思います.
詳しく検討するとタレスの業績には,後世の人々が,「哲学者や賢人はこうあるべきだ」と考え,思いを仮託していたことが分かります.
そのメッキを剥がしたとき,最後に残るのは,川の土木工事という実務家の側面.そして「無生物にも魂がある」ということと「万物の元のものは水である」という彼の学説のみが残されました.

https://www.youtube.com/watch?v=E9mCcYURaXI&t
