数学者のホンネ　森毅『線型代数　生態と意味』

　数学には、ホンネとタテマエがある。私がそう習ったのは高校のとき通っていた塾であり、微積分の微分係数を取り扱った授業であった。微分係数とはなにか。タテマエでは、それはどの教科書にも載っている、極限の記号limitを用いた微分係数の定義である。しかし、ホンネでは、微分係数とは、Δx≒0のときΔf≒AΔxであるAのことをいう。つまり、Δxが十分に小さいとき、fは正比例と考えられ、その比例係数が微分係数ということだ。

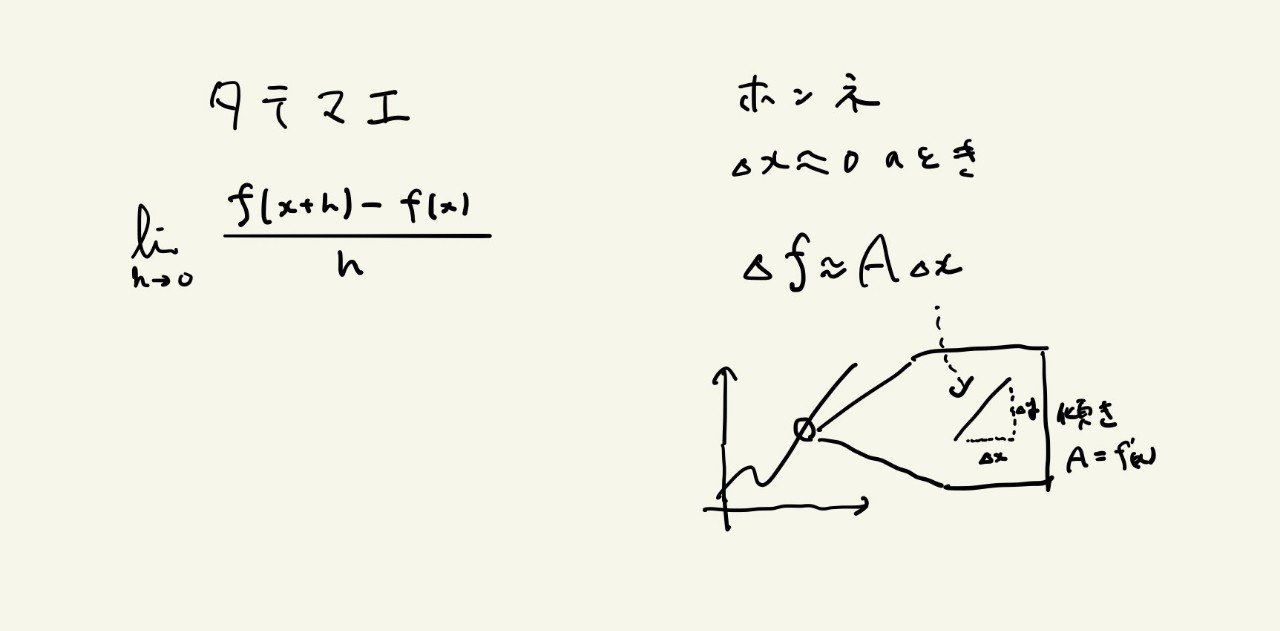
　タテマエは、数学的に正確であるが分かりにくい。一方、ホンネは数学には曖昧であるが意味が分かりやすい。本書は、正確さを保ちながらも線型代数のホンネを多く述べている。行列や内積、行列式、固有値などのホンネは何か、どういった意味を持つのか、それらを導入することで数学的にどういった広がりを生むことになるのか。そういった事柄を著者の独特の口調で語りかけてくれる。

　例えば、「線形代数とはなによりまず、《多次元の正比例》であるのだ。」がある。このようにシンプルにわかりやすく考えることで、y=Axにおいて「ベクトルというのは多次元の変数をヒトマトメにしたもの、行列というのは多次元の比例定数表をヒトマトメにしたもの」と解釈することができるのだ。このように理解することで、さまざまな数式に親近感が湧き、それが当たり前に思えるようになる。また、固有値問題を以下のように解釈する。「線型代数というと、〈まとめる〉ことのようだったが、当然のことに、まとめたものを、うまく〈ばらす〉ことが問題になるのである。」固有値問題を分解の問題と考えるのである。これによって、いかに分解するかに興味が湧くだろう。さらに、これを念頭に置くことで、その後の話の展開がスムーズに感じられるのである。

　本書は、線型空間の導入を早々に行うため、写像や関数の考えに慣れていないと戸惑うかもしれない。また、演算に対する言及が少ないため、それは他の本で補う必要がある。大学の授業で演算の練習はやったが、線型代数で自分が何をやっているか分からない人には、特にオススメだ。もちろん、数学好きの高校生、数式を扱う大学生、社会人も読むことを薦める。

　数式の意味やホンネを知ることで、自分の心の中の数学が広がっていく。そのワクワクこそ、数学の本質ではないだろうか。数学が嫌いな人は数学を好きになり、好きな人はもっと数学を好きになるはずだ。

2020/07/27加筆