中学受験の定番、旅人算を一発で解く裏技

我が家は息子が2022年2月に中学受験しました。

息子の受験勉強に伴走し、算数もみてきました。

中学受験算数といえば、特殊算です。

以前、ツルカメ算の裏技を紹介しました。

旅人算にも一瞬で答えを出す、裏技があります。

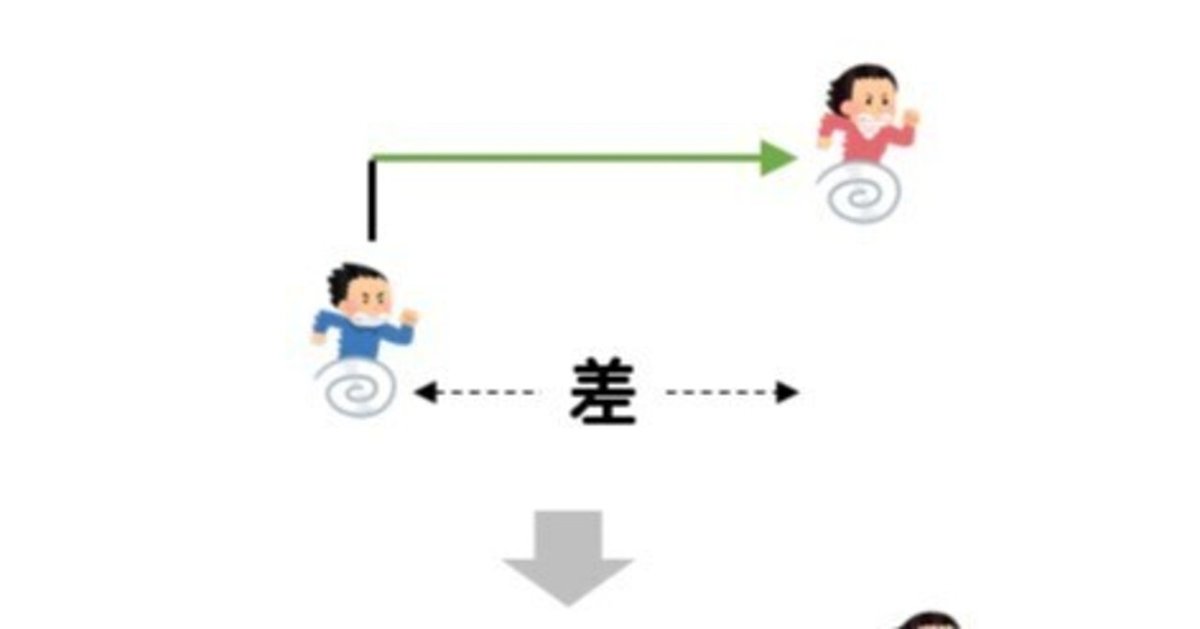
兄が家を出て分速80ｍで駅に向かい、兄が家を出て５分後に弟が家を出て分速100ｍで兄を追いかけたとき二人が出会うのは家から何ｍのところか、という問題で考えます。

普通、追いかける弟が出発するときの兄との距離、

つまり、80　×　5　＝　400ｍ

を、速度の差、分速20ｍで割ることにより、追い付くまでの時間が20分とわかるので、

追い付く地点は、100　×　20　＝2000ｍ　と求めます。

裏技は、問題に出てくる数字の80と5と100を全てかけて、これを速度の差20で割ると、一発で2000ｍと出ます。

マジックのようです。

本当は線分図を書くとわかりやすいですが、80と5をかけると、兄が5分間で進んだ距離（＝400ｍ）が出ます。

兄は分速80ｍ、弟は分速100ｍで進むので、弟が出発してから二人が出会うまでの移動距離をそれぞれ、80、100とおけます。

この差にあたる、20　が　80 × 5 （=400ｍ）に相当するので、

求める距離である100は、400を20でわって100倍すればよく、

これは100倍してから20で割っても同じです。

つまり80と5と100をかけて20で割ればいいことになります。

参考になりましたら幸いです。

【参考】比で考えることもできます。

弟が出発したとき、兄は既に400ｍ進んでいて、

兄と弟の速度の比が4：5なので、

兄と弟の移動距離も4：5になります。

4と5の差＝1が400ｍに相当するので、

弟の移動距離は、400×5＝2000

となります。