
国の借金が有限値に収束するモデル
タイトルには国の借金って書いたけど、語弊があるよね…政府債務ってことです。
この記事は!
「SFCモデル的な視点から経済を見た時、政府が機能的財政を完璧に行えれば政府債務が必ず一定の値に収束する」
という事を非常に単純化されたモデルをもって数学的に証明します。
ここではそれなりにわかっている前提でお話をしていきます。わからない人は頑張ってね
公理
完全雇用が達成されている閉鎖体系の世界を与えます。
このような世界では民間の支出は生産高と独立します。
よってGDPは自然成長率ずつ増えていきます。
では自然成長率を「n」と置いたら、時間「t」期におけるGDPは以下のように表せます。(一般項)
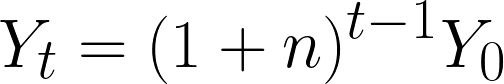
Y0は初項。
次に政府は完璧な機能的財政を行う事とし、政府の債務のみが民間にとっての唯一の金融資産と仮定します。
そうするといかなる政府債務(D)の増加は民間部門の金融資産(V)になります。
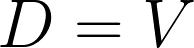
定理の導出
では任意の期間における可処分所得は、総生産から税金を引いた物と民間が持つ金融資産(=政府債務)からの金利収入の合計に等しくなります。
税金=τ、利子率=i
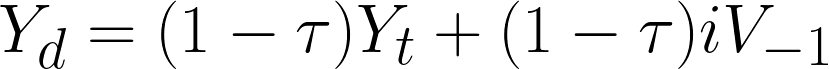
次に政府債務の変化量(=時間で微分したもの)は、可処分所得からの貯蓄量と金融資産からの消費量の差分に等しくなります。
なぜなら上記の仮定の下、機能的財政が完璧になされるという事は、いかなる民間貯蓄(=金融資産)も政府債務と同値にならなければいけないからです
マクロ経済全体の貯蓄性向=s、金融資産からの消費性向=c(0<s<1、0<c<1)
注意:上記の貯蓄性向と消費性向は別々のパラメーターです。
よって以下のように記述できます。
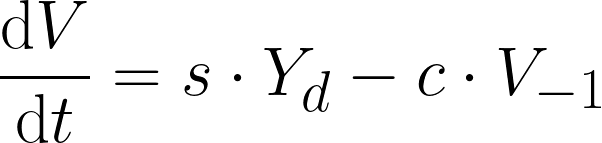
したがって可処分所得の式を上記の変化量の式に代入すれば、任意の期間における政府債務量の式に変形できます。

ではこの式を特性方程式をつかって特殊解をもとめてから、一般項を求めましょう。(急いでやったからわんちゃん間違ってるかも笑)
一般項は……

となります。
動学分析
では上記で求めた式を、横軸が時間、縦軸が貨幣単位($とか)のグラフに図示してみましょう。
グラフ:青線=GDP、赤線=政府債務量

上記のグラフは、政府債務ゼロ&自然成長率ゼロの場合を描画しています。
すると時間ともに政府債務が増えてゆきますが、だんだんとある程度のあたいで収束するのが見えるでしょう。
これは政府債務がGDPよりも大きい場合でも同様です。

組み合わせによっては普通にGDPより高い値に収束する事もあります。
(注意:GDPはフローを表すが、政府債務はストックである)

より詳細な分析:政府負債/GDP比率
主流派ではよく「政府債務とGDPの比」という概念用いられます。(役立たずな概念だけどさ、まあね……)
この概念を用いて上記のモデルの詳細な分析をしてましょう。
上記のモデルをもって任意の時間における政府債務/GDP比率を表すと……
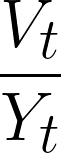
ですね。
グラフで描写すると……(縦が比率、横が時間)
(最初から政府債務がある程度ある場合を想定)

さて上記のグラフではターム1の時、債務・GDP比率は2(=200%)となっています。(債務/GDP比率200%は今の日本と同じくらい)
この場合も長期的には有限の値に収束しており、発散しません。
各パラメーターと収束値への影響
自然成長率の上昇→収束する速度が速くなります。(当然マイナスになれば遅くなる)
ただし組み合わせによっては、債務・GDP比率が低くなってから再度上昇するパターン、もしくはその逆もある(結論は同じ)
例↓

貯蓄性向の上昇→収束値が大きくなります。(資本が一期毎に蓄積する量が増えるから)
消費性向の上昇→収束値が小さくなります。(政府債務の民間主体からの減少速度が増加するため)
利子率の上昇→収束値が大きくなります。(すでに民間が持つ政府債務への利払いが増加、よって民間からの金融資産の減少速度が相対的に低下するため)
モデルの安定条件
色々と書いてきましたが、政府債務が有限の値に収束するには以下の条件が満たされる必要があります。
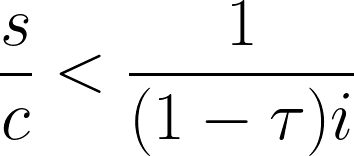
上の条件式だけ見てもよくわからないかもしれませんが、これは中々面白い事を示してくれます。
この条件が破られるようなパターンとは、金融資産を持つ層の消費性向が殆どない、つまり金融資産を消費しない(=政府に債務が戻ってゆかない)
加えて経済全体の貯蓄性向が非常に高く、その結果生じる穴を政府が埋めないといけない状態になっています。
よって金融資産を持つ層へのさらなる富の集中が起きてしまい、さらには資本家層への金利収入の増加も相まって収集がつかなくなってしまう。
という感じです。
またこの条件に成長率は一切登場しません。
これはたまに耳にする「国債利子率がGDP成長率を超えてしまったら政府債務が無限大になる~」っていうのは”嘘”って事がわかりますね。
金融資産からの消費性向は約5%程度,集計レベル貯蓄性向も20%以下であることが見積もられています。(Marc Lavoie. Post Keynesian Economics: new foundations. 2014)
なので利率10%といった非常に高い金利+成長率がゼロなんていう組み合わせでも何の問題もなく政府債務は収束します。
よって上記の式は、殆どすべての場合で満たされる可能性の高い条件と言えます。
結論
まず重要な結論の一つとして「政府は自らの債務量を選べない」という事が示されました。
なぜなら利子率である程度の調整を出来るとはいえども、最終的に債務量は民間主体の貯蓄&消費性向によって一方的に決まってしまうためです。
そのため支出を裁量的にバランスさせようとする試みは無意味なものになってしまうでしょう。
加えて成長率が機能的財政の制約にならない事も示されました。
負の成長率でも、正の成長率でも、はたまた成長してなかったとしても、債務/GDP比率は貯蓄&消費性向、利子率といった要因で決定され、成長率はその調整速度にしか影響を及ぼせません。
最後にモデルの安定条件は比較的盤石なもので、幅広い現実的な利率や貯蓄&消費性向の組み合わせの下であれば一般性を失わない事が示された。
以上より、完全雇用と安定条件を毎期満たす経済において、適切な機能的財政を政府が行う事が出来れば、必ず政府債務は有限の値に収束する事が証明できました。
