文系の僕がゼロから学ぶ統計-標準偏差、偏差値が意味するものとは-

ニュースの記事を見ながらたまに思ったことある方いますか？？

『標準偏差ってなんだっけ。。』

なんとなく、統計学の用語？？みたいなイメージありますが、ちゃんと説明できない方もいるのでは、、、そして僕もその中の一人です。

理系の方、数学をやってきた方であれば、ごくごく普通の教養かもしれません。最近コロナの関連のニュースで統計的な推計をしている記事等を見ていて、

「やっぱり、統計わからないとまずいかも。」

という、思いに至り記事を書くことにしました。ですので、今回の記事は当たり前の人にとっては基礎中の基礎の内容です。

ただ、もし僕のように高校、大学で数学すっとばしてしまって後悔している方には参考になるかと思います。

＜目次＞
■標準偏差って何？？
■標準偏差からわかること（正規分布）
■偏差値の意味

今回の参考文献はこちら。

完全独習 統計学入門

入門書ですが、ど文系の僕では一発目で100％理解できない点もありました、本当に理解したとこ、大切なところを見ていきます。

■標準偏差って何？？

標準偏差というのは、

各データが平均値に対してどの程度広がっているか、散らばっているかを評価する数値

です。既に頭から煙でてきそうなので、具体例を見ていきます。

たとえば、毎朝7時30分のバスに乗り通勤したいとして、A社とB社の２つのバス会社があったとします。どちらも平均の到着時刻は7時31分です。

と聞いたら、どっちでも良さそうだなーって感じがしますが、そこで考えるべきが標準偏差（Standard Devitaion)です。

仮に、A社とB社のバス到着時間が以下とすると、平均到着時刻は両社とも7時31分ですが、なんとなくA社の方が良さそうです。

表を見るとB社の方が平均値7時31分に対してばらつきが大きそうです。ただし、その差分（偏差）を足し算しても＋と－があるので０になってしまいます。

そこで、平均に対する差分を２乗してマイナスを打ち消します。それを更にデータの数（月ー金の合計５）で割り算した数値を【分散】といいます。

A社の分散が6.8、B社の分散20ですのでB社の方がばらつきが大きいといえそです。

しかし、分散の値（A社6.8）でバラツキを評価してしまうと、2乗しているために、実際には2－3分しかバラツキがないのに大きすぎてしまいます。

そこで、2乗していた分散の値(6.8）を平方根（ルート：2乗すると6.8になる数）にすることで、約2.6という数字になり、これを【標準偏差】と呼びます。

ですので、A社の場合は平均的にバスは時刻表より1分遅れて到着するが、実際の到着時刻はおおよそ2.6分内にちらばらっていると認識できます。

同じ平均値でもA社の標準偏差は2.6分、B社が4.5分ですのでA社のバスを選択するのがよい判断と言えます。

日ごろ、平均して物事を考えることはありますが、その平均値に対するバラツキ（標準偏差）を考えるとより件名な判断ができそうです。

■標準偏差からわかること（正規分布）

一般的にデータセットの素性がよければ、平均値から標準偏差プラス、マイナス1個分に約70％、2個以上離れるデータは約5％しかないといわれています。

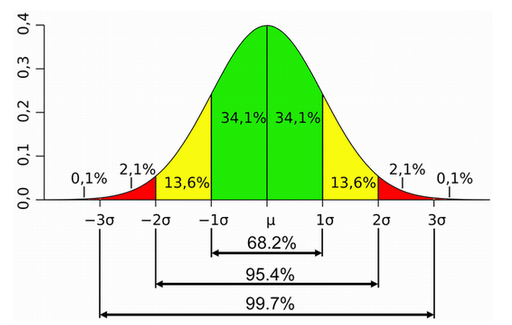
＊σ＝標準偏差

ですので、例えば

①平均点60点のテストで75点（平均＋15点）標準偏差12点
②平均点60点のテストで75点（平均＋15点）標準偏差8点

であれば、標準偏差8点に対して約2倍の点数を取っている②のケースの方が、立派な成績と言えます。

平均に対して同じように上回っていても、標準偏差において判断することが、正しく情報を判断するコツといえます。

■偏差値の意味

学生のおこさんをお持ちの方、またおこさん自身であれば、偏差値って何度も何度も聞かされます。

今回の模試の偏差値いくつだったの！？
今回の模試で偏差値が前回より4も下がっちゃった！！

など、一喜一憂してる方もいると思います。僕もこども頃がそうでした。

しかし、実は偏差値って

テストの平均点に対して偏差値50を与え、次に平均点から標準偏差１つ高くなるごとに10点を加点、低くなるごとに10点を減点しています。

例えば、平均点50点のテストで標準偏差が15点の場合。65点は偏差値60、　60点は偏差値56になります。

ですが、先ほどの正規分布に従えば「どちらも平均からよくあるずれ方」であることを意味しているだけで、そこまで拘るほどのことでもありません。

当然、あがったら褒めてあげてもよいと思いますが、下がってもあまり気にする必要はなさそうです。偏差値2－3の差は、よくあるずれ方の範囲内である意味偶然の所産です。

標準偏差というものを理解するだけでも、大きくものの見方って変わるなと、僕はひとつ学びになりました。

統計的な考え方を身につけると、より正しい、より良い判断ができるようになるかもしれません。

本日も読んでいただきありがとうございます。