
第13章「意外と他人は気にしてない」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング2」の第13章「意外と他人は気にしてない」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、心理学の「透明性の錯覚」という硬派なテーマを取り扱います。
例えば「大勢の前での発表のとき、自分はすごく緊張したのに、後から友人に訊いたら緊張しているように全然見えなかった、と言われた」という場合が、透明性の錯覚の現れです。

今回の PyMC化 は、テキストの結果と概ね一致しました!
ちょっぴり心理学に近づけた気がいたします。
ではでは、PyMCのベイズモデリングの世界を楽しんでまいりましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 永野駿太 先生
モデル難易度: ★★・・・ (やさしめ)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★★ & GoooD! \\
結果再現度 & ★★★★★ & 最高✨ \\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
今回はほとんど躓くこと無く、すんなりモデルを完成させられました。
テキストの文章や R スクリプトが読みやすかったからです。
勝手に錯覚しているだけかもしれませんが・・・
工夫・喜び・反省
データの外観を確認する集計表やグラフを添えてみました。
ちょっぴりデータ分析っぽいかもです。
勝手に錯覚しているだけかもしれませんが・・・2

モデルの概要
テキストの調査・実験の概要
■ 透明性の錯覚
テキストによると、透明性の錯覚は「実際以上に自身の内的状態が他者に見透かされていると感じる現象」です。
大勢の前でステージにたった私はとても緊張を感じているし、私を見ている眼前の人たちもきっと、私がとても緊張していると思っているに違いない。
見透かされている。見抜かれている。
透明性、つまり、自分の心が他者に透けている感覚とはきっと、こんな感じのことだと思います。
もうちょっと知りたい!という方には「錯思コレクション100」サイトさまの記事をご紹介いたします。
この章の実験に似た例題も掲載されています。

■ 実験で確認すること
透明性の錯覚は、「①私が行ったこと(主観的な体験)」と「②私が知っていること(解の既知性)」によって「③客観的な他者の視点」から乖離してしまい、実際以上に自分の内面が他者に伝わっていると感じること~こんなメカニズムをテキストは想定しています。
実験の目的は②「解の既知性」が透明性の錯覚に与える影響を確かめることです。
■ 実験の概要
透明性の錯覚を引き起こす実験内容は「私が飲んだ酸っぱい飲み物のことを、他の人も知っている…」です!
ポイントは「推測者グループ」。
推測者グループは、①「主観的な体験」は無いけれども、②「解の既知性」を持つ実験参加者です。
下の図で実験を概観してください!

行為者グループと推測者グループが「客観的な正答率を加味」しているのは、質問で「他者がどう考えるか」を問いかけているからです。

テキストのモデリング
テキストは2つのモデルを構築しています。
モデル1:グループに共通のパラメータを推定するモデル
行為者グループ、推測者グループ、観察者グループに共通するパラメータを推論します。
グループごと、または、実験参加者個人ごとのパラメータを考慮しないモデルです。
■ 目的変数と関心のあるパラメータ
目的変数は質問の回答値$${Y_{ij}}$$です。
添字$${i}$$は実験参加者ID、$${j}$$はグループです。
$${j=1}$$:行為者グループ、$${j=2}$$:推測者グループ、$${j=3}$$:観察者グループです。
関心のあるパラメータは、客観的な正答率$${\alpha_1}$$、解の既知性による影響$${\alpha_2}$$、主観的経験による影響$${\alpha_3}$$です。
■ モデル数式
添字$${p}$$は$${\alpha}$$の添字$${1,2,3}$$に対応しています。
$$
\begin{align*}
Y_{ij} &\sim \text{Binomial}\ (N_j,\ \theta_j) \\
N_j &= (10,\ 10,\ 1) \\
\\
\theta_j &= (\theta_1,\ \theta_2,\ \theta_3) \\
\theta_1 &= \alpha_1 + \alpha_2 + \alpha_3 \\
\theta_2 &= \alpha_1 + \alpha_2 \\
\theta_3 &= \alpha_1 \\
\\
\alpha_1,\ \alpha_2,\ \alpha_3 &= \alpha_p[1],\ \alpha_p[2],\ \alpha_p[3] \\
\\
\alpha_p &= \psi \cdot \omega_p \\
\psi &\sim \text{Uniform}\ (0,\ 1) \\
\omega_p &= \text{softmax}\ (\omega_p^*) \\
\omega_p^* &\sim \text{Normal}\ (0,\ 1) \\
\end{align*}
$$
最後の段落に注目です。
$${0 \leq \alpha_1 + \alpha_2 + \alpha_3 \leq 1}$$の制約を実現するための数式です。
$${\psi = \alpha_1 + \alpha_2 + \alpha_3}$$と置き、$${\psi \sim \text{Uniform}\ (0,\ 1)}$$として$${\psi}$$の範囲を0~1にしています。
さらにsoftmax関数で重み$${\omega_1,\ \omega_2,\ \omega_3}$$を合計1(つまり3つの$${\omega}$$は按分比率)になるように調整して、$${\psi \cdot \omega_p}$$で3つの$${\alpha}$$(合計が0~1の間)を求めています。

モデル2:個人差を構造化する階層モデル
行為者ごとの個人差を構造化するモデルです。
■ 目的変数と関心のあるパラメータ
目的変数は質問の回答$${Y_{ijk}}$$です。
添字$${i}$$は実験参加者ID、$${j}$$は3つグループの識別子、$${k}$$は行為者IDです。
関心のあるパラメータは、行為者の個人差を切り分けた後の客観的な正答率$${\mu_{\alpha_1}}$$、解の既知性による影響$${\mu_{\alpha_2}}$$、主観的経験による影響$${\mu_{\alpha_3}}$$です。
■ モデル数式
$${\Phi(\cdot)}$$はプロビット変換です。
$$
\begin{align*}
Y_{ijk} &\sim \text{Binomial}\ (N_j,\ \theta_{jk}) \\
N_j &= (10,\ 10,\ 1) \\
\\
\theta_{jk} &= (\theta_{1k},\ \theta_{2k},\ \theta_{3k}) \\
\theta_{1k} &= \alpha_{1k} + \alpha_{2k} + \alpha_{3k} \\
\theta_{2k} &= \alpha_{1k} + \alpha_{2k} \\
\theta_{3k} &= \alpha_{1k} \\
\\
\alpha_{1k},\ \alpha_{2k},\ \alpha_{3k} &= \alpha_{pk}[1],\ \alpha_{pk}[2],\ \alpha_{pk}[3] \\
\alpha_{pk} &= \psi_k \cdot \omega_{pk} \\
\\
\psi_k &\sim \Phi\ (\psi_k^*) \\
\psi_k^* &\sim \text{Normal}\ (\mu_{\psi^*},\ \tau_{\psi^*}) \\
\\
\omega_{pk} &= \text{softmax}\ (\omega_{pk}^*) \\
\omega_{pk}^* &= (\omega_{1k}^*,\ \omega_{2k}^*,\ \omega_{3k}^*) \\
\omega_{1k}^* &\sim \text{Normal}\ (\mu_{\omega_1^*}, \tau_{\omega_1^*}) \\
\omega_{2k}^* &\sim \text{Normal}\ (\mu_{\omega_2^*}, \tau_{\omega_2^*}) \\
\omega_{3k}^* &\sim \text{Normal}\ (\mu_{\omega_3^*}, \tau_{\omega_3^*}) \\
\\
\mu_{\psi^*},\ \mu_{\omega_1^*},\ \mu_{\omega_2^*},\ \mu_{\omega_3^*} &\sim \text{Normal}\ (0,\ 1) \\
\tau_{\psi^*},\ \tau_{\omega_1^*},\ \tau_{\omega_2^*},\ \tau_{\omega_3^*} &\sim \text{Normal}\ (0,\ 10) \\
\\
\mu_{\alpha_p} &= \mu_{\psi} \cdot \mu_{\omega_p} \\
\mu_{\psi} &= \Phi\ (\mu_{\psi^*}) \\
\mu_{\omega_p} &= \text{softmax}\ (\mu_{\omega_p^*}) \\
\end{align*}
$$
興味のあるパラメータ$${\mu_{\alpha_p}=(\mu_{\alpha_1},\ \mu_{\alpha_2},\ \mu_{\alpha_3})}$$は最後の段落で算出しています。
行為者個人$${k}$$の$${\psi_k^*,\ \omega_{pk}^*}$$の従う正規分布の平均パラメータ$${\mu_{\psi^*},\ \mu_{\omega_p^*}}$$が全体の平均値となり、この平均パラメータを用いて$${\mu_{\alpha_{p}}}$$を導出しています。

■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込みと前処理
csvファイル「dat.csv」をpandasのデータフレームに読み込みます。
### データの読み込み
data = pd.read_csv('dat.csv')
display(data)【実行結果】
項目内容の概要です。
・ID:実験参加者ID
・Actor:行為者の実験参加者ID
・Y:実験参加者の回答値(目的変数)
・Group:実験参加者が所属するグループ
(1:行為者グループ、2:推測者グループ、3:観察者グループ)
・N:尤度関数の二項分布の試行回数パラメータに使える値

3.データの概観の確認
実験に参加した各グループの人数を見てみます。
### 各グループの人数
(data.drop_duplicates(subset=['ID', 'Group'])['Group'].value_counts()
.sort_index().to_frame())【実行結果】
行為者グループ:12人、推測者グループ:29人、観察者グループ:29人です。
行為者グループと推測者グループは「10人中何人が当てられるか」を回答しています。
回答の分布を見てみましょう。
### 行為者グループと推測者グループの予測人数の描画
# 箱ひげ図の描画
sns.boxplot(data=data[data['Group'].isin([1, 2])], x='Group', y='Y',
color='tab:blue', fill=False)
# スウォームプロットの描画
sns.swarmplot(data=data[data['Group'].isin([1, 2])], x='Group', y='Y',
color='tomato', alpha=0.3)
# 修飾
plt.xticks(ticks=[0, 1], labels=['行為者グループ', '推測者グループ'])
plt.ylabel('正確に当てられると予測した人数(最大10人)');【実行結果】
当てると予測した人数の平均値は行為者グループの方が大きいです。
また最小値も行為者グループの方が大きくて、誰も当てない(0人)とする回答はありませんでした。
こ、こ、これは「透明性の錯覚」の発現でしょうか?

観察者グループの回答の正答率を確認しましょう。
### 観察者グループの正答率の算出
(data[data['Group']==3]['Y'] # 観察者グループ(Group==3)の列Yを抽出
.value_counts(normalize=True) # Yの値の比率(normalize=True)を算出
.to_frame() # データフレーム化
.set_axis(['誤答', '正答'], axis=0) # インデックス名の設定
.set_axis(['割合(%)'], axis=1) # 列名の設定
.round(3) * 100) # 比率を四捨五入で小数第3位に丸めて100倍【実行結果】
映像を見て味の異なる飲み物の番号を当てた正答率は約 24% です。
行為者グループ 12 人中、3 人くらいを「当てた」ようです。

行為者ごとに正答・誤答の数を見てみましょう。
### 行為者ID別正答・誤答数の描画
# カウントプロット(棒グラフ)の描画
sns.countplot(data=data[data['Group']==3], x='Actor', hue='Y', palette='Pastel1')
# 修飾
plt.xlabel('飲み物を摂取した行為者ID')
plt.ylabel('誤答・正答の数')
plt.legend(title='味の異なる飲み物を当てられたか', labels=['誤答', '正答'],
ncol=2, bbox_to_anchor=(0, 1.18), loc='upper left');【実行結果】
ID3 の行為者はよく当てられているようです。
その他の行為者は誤答の方が多いようです。


モデル1:グループに共通のパラメータを推定するモデル
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\begin{align*}
\psi &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1) \\
\omega^* &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=1,\ \text{dims}=factor)\\
\omega &= \text{softmax}\ (\omega^*),\ \text{dims}=factor \\
\alpha &= \psi \times \omega,\ \text{dims}=factor\\
\theta &= [\alpha[0] + \alpha[1] + \alpha[2],\ \alpha[0] + \alpha[1],\ \alpha[0]],\ \text{dims}=group \\
likelihood &\sim \text{Binomial}\ (\text{n}=N,\ \text{p}=\theta[groupIdx]) \\
\end{align*}
$$
1.モデルの定義
データの前処理を行います。
インデックス化とラベル作成です。
## インデックスとラベルの作成
# Group
group_idx = data['Group'] - 1 # 0始まり化
group_label = ['行為者', '推測者', '観察者']
# αの要素
factor_label = ['客観的な正答率', '解の既知性', '主観的経験']
# Actor
actor_idx = data['Actor'] - 1 # 0始まり化
actor_label = sorted(data['Actor'].unique())続いて数式表現を実直にモデル記述します。
### モデルの定義
with pm.Model() as model1:
## coordの定義
# データのインデックス
model1.add_coord('data', values=data.index, mutable=True)
# グループ:行為者・推測者・観察者のラベル
model1.add_coord('group', values=group_label, mutable=True)
# αの要素:客観的な正答率・解の既知性・主観的経験のラベル
model1.add_coord('factor', values=factor_label, mutable=True)
## dataの定義
# 回答Y
Y = pm.ConstantData('Y', value=data['Y'].values, dims='data')
# 試行数N
N = pm.ConstantData('N', value=data['N'].values, dims='data')
# Groupインデックス
groupIdx = pm.ConstantData('groupIdx', value=group_idx, dims='data')
## 事前分布
## α
# ψ:α0~α2の合計
psi = pm.Uniform('psi', lower=0, upper=1)
# ω*:ωの要素
omegaAster = pm.Normal('omegaAster', mu=0, sigma=1, dims='factor')
# ω:ψに対するα0~α2の重み(ω*にsoftmax関数を適用して合計1の確率値に変換)
omega = pm.Deterministic('omega', pm.math.softmax(omegaAster),
dims='factor')
# 客観的な正答率α0, 解の既知性による影響α1, 主観的経験による影響α2
alpha = pm.Deterministic('alpha', psi * omega, dims='factor')
## 確率θ
# 行為者の推測する見透かされる確率θ0, 推測者の推測θ1, 観察者の客観的な正答率θ2
theta = pm.Deterministic('theta',
pt.stack([alpha[0] + alpha[1] + alpha[2],
alpha[0] + alpha[1],
alpha[0]]),
dims='group')
## 尤度
likelihood = pm.Binomial('likelihood', n=N, p=theta[groupIdx], observed=Y,
dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の3つを設定しました。データの行の座標:名前「data」、値「行インデックス」
グループの座標:名前「group」、値「(行為者, 推測者, 観察者)」
$${\alpha}$$の要素の座標:名前「factor」、値「(客観的な正答率, 解の既知性, 主観的経験)」
dataの定義
次の3つを設定しました。回答値:Y (目的変数)
試行回数:N
グループのインデックス:groupIdx
パラメータの事前分布
モデルの数式表現のとおりです。
尤度
試行回数パラメータが試行回数$${N}$$、成功確率パラメータが確率$${\theta}$$の二項分布です。
2.モデルの外観の確認
### モデルの表示
model1【実行結果】
Deterministic:決定論的変数が多いかもです。

### モデルの可視化
pm.model_to_graphviz(model1)【実行結果】

3.事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ1分でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 1分
# テキスト: iter=105000, warmup=5000, chains=4, thin=10
with model1:
idata1 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=123)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata1 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
var_names = ['alpha', 'theta', 'psi', 'omega', 'omegaAster']
pm.summary(idata1, hdi_prob=0.95, var_names=var_names, round_to=3)【実行結果】

トレースプロットで事後分布サンプリングデータの様子を確認します。
### トレースプロットの表示
pm.plot_trace(idata1, var_names=var_names, compact=True)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

5.推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata1 をpickleで保存します。
### idataの保存 pickle
file = r'idata1_ch13.pkl'
with open(file, 'wb') as f:
pickle.dump(idata1, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata1_ch13.pkl'
with open(file, 'rb') as f:
idata1_load = pickle.load(f)◆ ◆ ◆ ◆ ◆
モデル1の分析
テキストには未掲載ですが、モデル1の推論結果を少々堪能いたしましょう。
ひとまず pm.summary() で出力できる統計量で注目するパラメータを見ておきましょう。
### 推論データαの要約統計情報の表示
var_names = ['alpha']
pm.summary(idata1, hdi_prob=0.95, var_names=var_names, kind='stats', round_to=3)【実行結果】
解の既知性による影響は平均値$${0.102}$$(95%HDI$${[0.058,\ 0.179]}$$)です。
解の既知性による正の影響が見られました。
なお平均値は、主観的経験による影響とほぼ同じです。
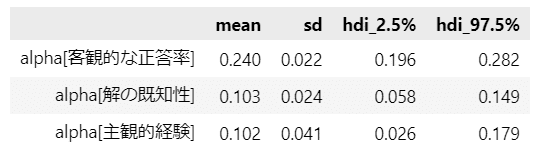
パラメータ$${\alpha}$$の事後分布を可視化しましょう。
### αの描画
pm.plot_posterior(idata1, var_names=['alpha'], hdi_prob=0.95, round_to=3)
plt.tight_layout();【実行結果】
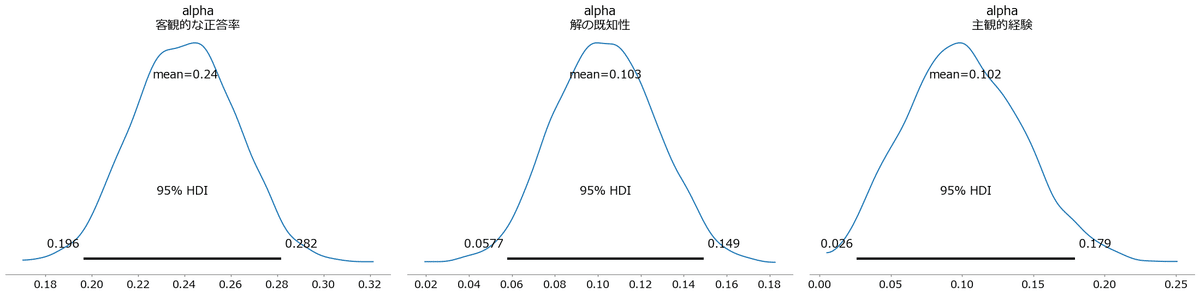
テキスト図13.2のような3パラメータの事後分布のヒストグラムを描画します。
### αの描画2
# 描画領域の設定
fig, ax = plt.subplots(3, 1, figsize=(10, 8), sharex=True, sharey=True)
# 3つのαの描画を繰り返し処理
for i in range(3):
# ヒストグラムの描画
sns.histplot(idata1.posterior.alpha.stack(sample=('chain', 'draw'))[i],
bins=30, kde=True, stat='density', ec='white', ax=ax[i])
# 修飾
ax[i].set(xticks=np.arange(0, 1.1, 0.1), ylabel='確率密度',
title=rf'$\mu_{{\alpha_{i}}}$ {factor_label[i]}')【実行結果】


モデル2:個人差を構造化する階層モデル
テキストは Stan の実装上、「Matt trick」という再パラメータ化を用いています。
この記事のモデルも Stan の実装にならって再パラメータ化を取り入れています。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\begin{align*}
\mu_{\psi^*} &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=1) \\
\tau_{\psi^*} &\sim \text{HalfNormal}\ (\text{sigma}=10) \\
\tilde{\psi^*} &= \text{Normal}\ (\text{mu}=0,\ \text{sigma}=1,\ \text{dims}=actor) \\
\psi^* &= \mu_{\psi^*} + \tau_{\psi^*} \times \tilde{\psi^*},\ \text{dims}=actor \\
\psi &= \text{invprobit}\ (\psi^*),\ \text{dims}=actor \\
\\
\mu_{\omega^*} &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=1,\ \text{dims}=factor) \\
\tau_{\omega^*} &\sim \text{HalfNormal}\ (\text{simga}=10,\ \text{dims}=factor) \\
\tilde{\omega^*} &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=1,\ \text{dims}=(actor,\ factor)) \\
\omega^* &= \mu_{\omega^*} + \tau_{\omega^*} \times \tilde{\omega^*},\ \text{dims}=(actor,\ factor)\\
\omega &= \text{softmax}\ (\omega^*),\ \text{dims}=(actor,\ factor) \\
\\
\alpha &= (\psi \times \omega^{\top})^{\top},\ \text{dims}=(actor,\ factor) \\
\\
\theta_0 &= \alpha[:,\ 0] + \alpha[:,\ 1] + \alpha[:,\ 2] \\
\theta_1 &= \alpha[:,\ 0] + \alpha[:,\ 1] \\
\theta_2 &= \alpha[:,\ 0] \\
\theta &= [\theta[0],\ \theta[1],\ \theta[2]]^{\top},\ \text{dims}=(actor,\ group) \\
\\
likelihood &\sim \text{Binomial}\ (\text{n}=N,\ \text{p}=\theta[actorIdx,\ groupIdx]) \\
\\
\mu_{\psi} &= \text{invprobit}\ (\mu_{\psi^*}) \\
\mu_{\omega} &= \text{softmax}\ (\mu_{\omega^*}),\ \text{dims}=factor \\
\mu_{\alpha} &= \mu_{\psi} \times \mu_{\omega},\ \text{dims}=factor \\
\end{align*}
$$
1.モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義
with pm.Model() as model2:
## coordの定義
# データのインデックス
model2.add_coord('data', values=data.index, mutable=True)
# グループ:行為者・推測者・観察者のラベル
model2.add_coord('group', values=group_label, mutable=True)
# 行為者IDのラベル 全12人
model2.add_coord('actor', values=actor_label, mutable=True)
# αの要素:客観的な正答率・解の既知性・主観的経験のラベル
model2.add_coord('factor', values=factor_label, mutable=True)
## dataの定義
# 回答Y
Y = pm.ConstantData('Y', value=data['Y'].values, dims='data')
# 試行数N
N = pm.ConstantData('N', value=data['N'].values, dims='data')
# Groupインデックス
groupIdx = pm.ConstantData('groupIdx', value=group_idx, dims='data')
# 行為者Actorインデックス
actorIdx = pm.ConstantData('actorIdx', value=actor_idx, dims='data')
## 事前分布
# ψ
muPsiAster = pm.Normal('muPsiAster', mu=0, sigma=1)
tauPsiAster = pm.HalfNormal('tauPsiAster', sigma=10)
psiAsterTilde = pm.Normal('psiAsterTilde', mu=0, sigma=1, dims='actor')
psiAster = pm.Deterministic('psiAster',
muPsiAster + tauPsiAster * psiAsterTilde, dims='actor')
psi = pm.Deterministic('psi', pm.invprobit(psiAster), dims='actor')
# ω
muOmegaAster = pm.Normal('muOmegaAster', mu=0, sigma=1, dims='factor')
tauOmegaAster = pm.HalfNormal('tauOmegaAster', sigma=10, dims='factor')
omegaAsterTilde = pm.Normal('omegaAsterTilde1', mu=0, sigma=1,
dims=('actor', 'factor'))
omegaAster = pm.Deterministic('omegaAster',
muOmegaAster + tauOmegaAster * omegaAsterTilde,
dims=('actor', 'factor'))
omega = pm.Deterministic('omega', pm.math.softmax(omegaAster, axis=1),
dims=('actor', 'factor'))
# 客観的な正答率α0, 解の既知性による影響α1, 主観的経験による影響α2
alpha = pm.Deterministic('alpha', (psi * omega.T).T,
dims=('actor', 'factor'))
## 確率θ
# 行為者の推測する見透かされる確率θ0, 推測者の推測θ1, 観察者の客観的な正答率θ2
theta0 = alpha[:, 0] + alpha[:, 1] + alpha[:, 2]
theta1 = alpha[:, 0] + alpha[:, 1]
theta2 = alpha[:, 0]
theta = pm.Deterministic('theta',
pt.stack([theta0, theta1, theta2]).T,
dims=('actor', 'group'))
## 尤度
likelihood = pm.Binomial('likelihood', n=N, p=theta[actorIdx, groupIdx],
observed=Y, dims='data')
### 計算値
muPsi = pm.Deterministic('muPsi', pm.invprobit(muPsiAster))
muOmega = pm.Deterministic('muOmega', pm.math.softmax(muOmegaAster),
dims='factor')
muAlpha = pm.Deterministic('muAlpha', muPsi * muOmega, dims='factor')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の4つを設定しました。データの行の座標:名前「data」、値「行インデックス」
グループの座標:名前「group」、値「(行為者, 推測者, 観察者)」
行為者の座標:名前「actor」、値「行為者ID」
$${\alpha}$$の要素の座標:名前「factor」、値「(客観的な正答率, 解の既知性, 主観的経験)」
dataの定義
次の4つを設定しました。回答値:Y (目的変数)
試行回数:N
グループのインデックス:groupIdx
行為者のインデックス:actorIdx
パラメータの事前分布
モデルの数式表現のとおりです。
尤度
試行回数パラメータが試行回数$${N}$$、成功確率パラメータが確率$${\theta}$$の二項分布です。
計算値
興味のあるパラメータ$${\mu_{\alpha}}$$を算出しています。
2.モデルの外観の確認
# モデルの表示
model2【実行結果】
横に長~いです。

### モデルの可視化
pm.model_to_graphviz(model2)【実行結果】
かなり複雑になりました。

3.事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ1分でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 1分
# テキスト: iter=105000, warmup=5000, chains=4, thin=10, adapt_delta=0.99
with model2:
idata2 = pm.sample(draws=1000, tune=2000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=123)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata2 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum()【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata2, hdi_prob=0.95, round_to=3)【実行結果】
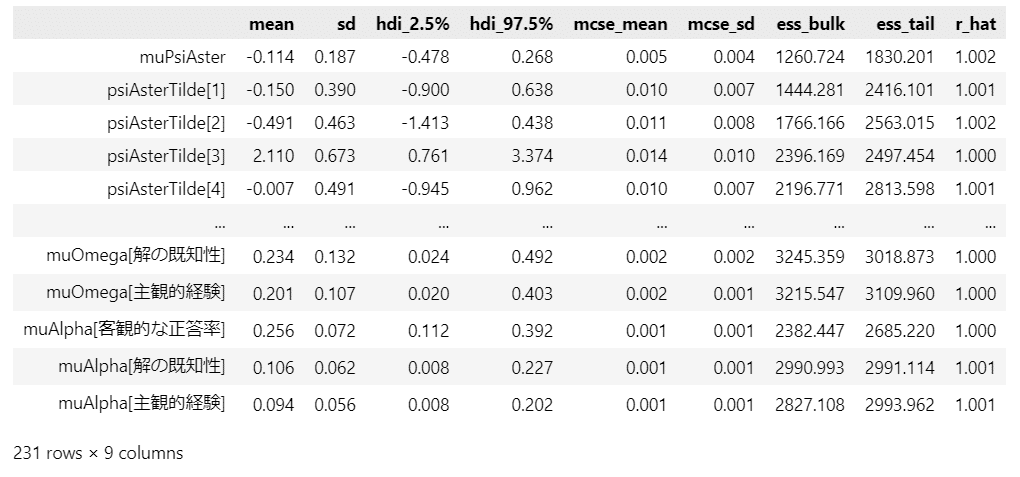
トレースプロットで事後分布サンプリングデータの様子を確認します。
### トレースプロットの表示
pm.plot_trace(idata2, compact=True)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
ただし、若干、発散(バーコード)が見られます。

5.推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata2 をpickleで保存します。
### idataの保存 pickle
file = r'idata2_ch13.pkl'
with open(file, 'wb') as f:
pickle.dump(idata2, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata2_ch13.pkl'
with open(file, 'rb') as f:
idata2_load = pickle.load(f)◆ ◆ ◆ ◆ ◆
モデル2の分析~テキストにならって
注目するパラメータ$${\mu_{\alpha_{p}}}$$を見ておきましょう。
図13.2に添えられた事後統計量を代替するものです。
### 推論データμ_αpの要約統計情報の表示 ※図13.2に掲載の事後統計量に相当
var_names = ['muAlpha']
pm.summary(idata2, hdi_prob=0.95, var_names=var_names, kind='stats', round_to=3)【実行結果】
解の既知性による影響は平均値$${0.106}$$(95%HDI$${[0.008,\ 0.227]}$$)です。
解の既知性による正の影響が見られました。

モデル1と比べるとバラツキ(標準偏差)がやや大きいようです。
(参考:モデル1の事後統計量)

$${\mu_{\alpha_{p}}}$$の事後分布のヒストグラムを描画します。
テキスト図13.2に相当します。
### μ_αpの事後分布の描画 ※図13.2に相当
fig, ax = plt.subplots(3, 1, figsize=(10, 8), sharex=True, sharey=True)
for i in range(3):
sns.histplot(idata2.posterior.muAlpha.stack(sample=('chain', 'draw'))[i],
bins=30, kde=True, stat='density', ec='white', ax=ax[i])
ax[i].set(xticks=np.arange(0, 1.1, 0.1), ylabel='確率密度',
title=rf'$\mu_{{\alpha_{i}}}$ {factor_label[i]}')【実行結果】
テキストの図と形状はよく似ています。

【分析~テキストにならって】
解の既知性によって引き起こされる錯覚の大きさの程度は、平均的には$${0.106}$$であり、95%HDIは$${[0.008,\ 0.227]}$$です。
つまり「解の既知性が透明性の錯覚の生起過程に影響を与えている」ことが示唆されました。
また、解の既知性が与える錯覚の大きさは、今回の実験に関しては客観的な正答率に加えて、平均的に$${10\%}$$程度多く見積もってしまうほどの大きさであることが示唆されました。
実験の設計とベイズモデリングがピタリと当てはまって、目に見えない確率が浮き彫りになったこと、とても感動しました!

以上で第13章は終了です。
おわりに
大勢の人の前で発表すること
最近は大勢の人の前で発表することが無くなりました。
特に新型ウィルスの感染拡大を機に「オンライン」でのコミュニケーションが主流になった感じがします。
提案や報告会は「オンライン」の向こうの人たちに対して行われるようになり、「人前」(ひとまえ)の概念が少し変わった感じもいたします。
オンラインの方が緊張しないのは何故でしょう?
「直接的に視線を浴びたり、表情の変化を目の当たりにすること」などが緊張の源泉なのかもしれませんね。
おわり
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
