
実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で⑩空間自己回帰モデル:2次元の株数カウントデータ
「時系列・空間データのモデリング」章
テキスト「時系列・空間データのモデリング」の執筆者
伊東宏樹 先生
この記事は、テキストの「時系列・空間データのモデリング」章の「アラカシの株数カウントデータを用いた空間自己回帰モデル」の実践を取り扱います。
空間的に自己相関のある 2次元データに対して、条件付き自己回帰モデル(Intrinsic CARモデル)を用いた推論を行います。
たのしくPyMCモデリングを進めましょう!
この章を執筆された伊東先生は「たのしいベイズモデリング2」第5章を執筆されています。
樹木の直径と高さの数理モデルをベイズに取り込んでいます!
こちらもお楽しみくださいませ。
はじめに
岩波データサイエンスVol.1の紹介
この記事は書籍「岩波データサイエンス vol.1」(岩波書店、以下「テキスト」と呼びます)の特集記事「ベイズ推論とMCMCのフリーソフト」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
テキストは、2015年10月に発売され、ベイズモデリングの様々なソフトウェアを用いたモデリング事例を多数掲載し、ベイズモデリングの楽しさを紹介する素晴らしい書籍です。
入門的なモデルから2次階差を取り扱う空間モデルまで、幅広い難易度のモデルを満喫できます!
このシリーズは、テキストのベイズモデルをPyMC Ver.5に書き換えて実践します。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「岩波データサイエンス vol.1」
第9刷、編者 岩波データサイエンス刊行委員会 岩波書店
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
PyMC環境の準備
Anacondaを用いる環境構築とGoogle ColaboratoryでPyMCを動かす方法について、次の記事にまとめています。
「PyMCを動かすまでの準備」章をご覧ください。
PythonとPyMC
テキストで利用するツールは、R、BUGS、JAGS 等です。
この記事では、PythonとPyMCを用いたコードに変換してベイズモデリングを実践いたします。
イントロ
1. モデルのイメージ
■ 2次元のCARモデル
前回は1次元のCARモデルをPyMCのICARで実装しました。
2次元のCARモデルもICARで実装できます!
2次元空間(平面)を扱えるとモデルの表現度が高まるような気がします!
CARモデルの詳細は前回記事をご参照くださいね★

■ 分析対象データ
伊東先生が収集したデータを用います。
京都市内の森林における「アラカシ」(カシの木の一種)の株数カウントデータです。
X方向100m、Y方向50mの調査区画の中を5m X 5m の小区画に分割(全200小区画)し、小区画ごとに株数をカウントしたデータです。
■ アラカシ
ウィキペディアによると、アラカシは常緑広葉樹で、高さが10~20mになるそうです。
そしてそしてドングリのなる木なのです!

ではでは、前回と同様に「重みとお隣さんに注目」して、次に進みましょう。
2. インポート
「時系列・空間データのモデリング」章で利用するパッケージをインポートします。
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# 確率統計
import statsmodels.formula.api as smf
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# WEBアクセス
import requests
# Rdata読み込み
import pyreadr
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')3. データの読み込み
CSVファイルをpandasのデータフレームに読み込みます。
### データの読み込み
# X方向100m・Y方向50mの範囲に5×5mの区画を設け、区画ごとにアラカシの株数Nをカウント
data3 = pd.read_csv('./data/Qglauca.csv')
display(data3)【実行結果】
X方向とY方向の組み合わせ(番地みたいな感じ)で小区画を識別します。
Xの1番目、Yの1番目の小区画は、株数N=0本です。

4. データの外観の確認
2次元ということで「ヒートマップ」で株数の濃淡を表現します。
テキストの図10に相当します。
seaborn の heatmap() を利用します。
### ヒートマップの描画 ※図10に相当
# 描画用データの作成 ※Y・Xの二次元に変換
data3_plot = data3.pivot_table(index='Y', columns='X', values='N')
# 描画領域の指定
plt.figure(figsize=(10, 4))
# ヒートマップの描画
sns.heatmap(data3_plot, cmap='Greens', square=False, cbar_kws={'label': '株数'})
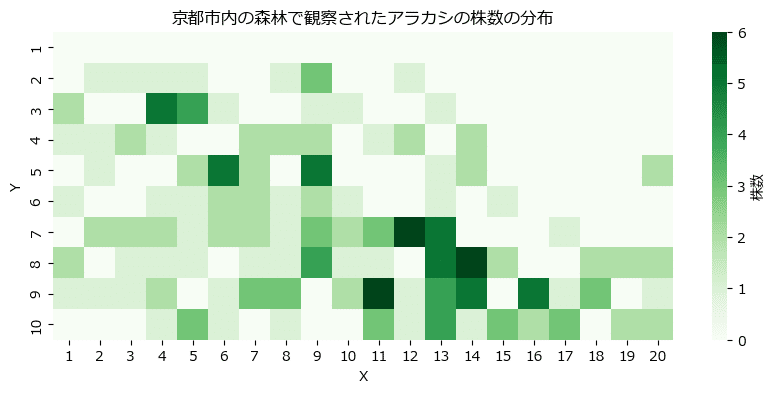
# 修飾
plt.title('京都市内の森林で観察されたアラカシの株数の分布');【実行結果】
色の濃い「X=11~14、Y=7~9」あたりに多く生息しているようです。
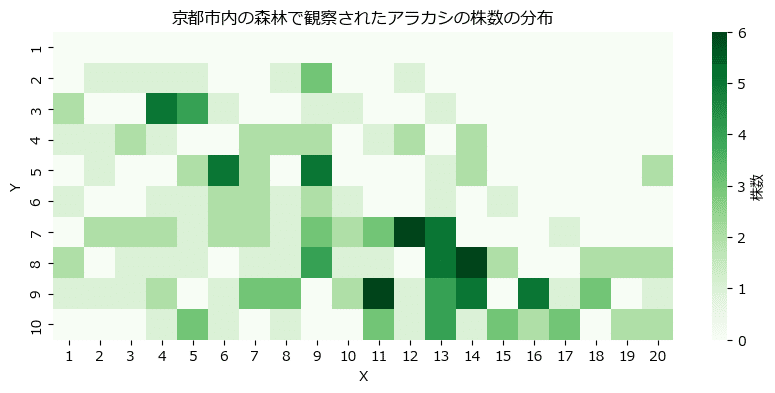
では、PyMCモデリングに進みます。

ベイズモデル
1. モデルの定義
まず最初に重みづけデータを作成します。
テキストでは「隣接行列」と呼んでいます。
PyMCでは ICARクラスの引数 w に隣接行列を指定します。
ロジックはとても難解です。ぜひテキストで確認してください。
### 隣接行列Wの作成 テキストのRコードを転用
# x方向の区画数
n_x = data3.X.max() # 20
# y方向の区画数
n_y = data3.Y.max() # 10
# 全区画数
n_sites = n_x * n_y # 200
# 隣接行列W2の生成 shape=(200, 200)
W2 = np.zeros((n_sites, n_sites))
for x in range(0, n_x):
for y in range(1, n_y+1):
if x > 0:
W2[x * n_y + y - 1, (x - 1) * n_y + y - 1] = 1
if x < n_x - 1:
W2[x * n_y + y - 1, (x + 1) * n_y + y - 1] = 1
if y > 1:
W2[x * n_y + y - 1, x * n_y + y - 1 - 1] = 1
if y < n_y:
W2[x * n_y + y - 1, x * n_y + y + 1 - 1] = 1
# 隣接行列W2の外観表示
print('W2.shape: ', W2.shape)
print(W2)【実行結果】
小区画200箇所×200箇所のマトリクスになりました。

■ 見方
行を起点区画($${i}$$)、列をお隣さん判定($${j}$$)と見立てます。
1行目は区画1です。お隣さんは値「1」が立っている列2=区画2です。
2行目は区画2です。お隣さんは値「1」が立っている区画1と区画3です。
PyMCのモデルを定義しましょう。
テキストによると「Intrinsic CARモデルによるランダム効果と切片のみのモデルをあてはめる」としています。
Intrinsic CAR モデルは ICAR クラスで実装します。
観測データが2次元になりましたが、モデルの内容は前回の1次元のケースと良く似ています。
### モデルの定義
with pm.Model() as model8:
### データ関連定義
# coordの定義
model8.add_coord('data', values=data3.index, mutable=True)
# dataの定義 観測値N
N = pm.ConstantData('N', value=data3.N.values, dims='data')
### 事前分布
# 切片
beta = pm.Normal('beta', mu=0, sigma=100)
# 標準偏差
sigma = pm.Uniform('sigma', lower=0, upper=100)
### 切片β+空間構造を取り入れたランダム効果Sのモデル
# 非中心配置のパラメータ化:ICARの標準偏差を1にして、結果のSにsigmaを乗ずる
S = pm.ICAR('S', W=W2, sigma=1, dims='data')
logLam = pm.Deterministic('logLam', beta + S*sigma, dims='data')
### 尤度:ポアソン分布
lam = pm.Deterministic('lam', pt.exp(logLam), dims='data')
Y = pm.Poisson('Y', mu=lam, observed=N, dims='data')■ モデルの注釈
ランダム効果$${S}$$には pm.ICAR() クラスを用いました。
PyMC公式サイトによる「標準偏差の設定」の仕方について補足します。
確率分布 ICAR の標準偏差$${\sigma}$$を ICAR の標準偏差 sigma 引数に設定せず、次のように分離して設定する「非中心配置のパラメータ化」です。
pm.ICAR() では標準偏差に1を設定する。
pm.ICAR() の結果変数である$${S}$$を次式の logLam で使用する際、$${S}$$に標準偏差$${\sigma}$$を乗じます。
また、$${\beta}$$と$${S,\ \sigma}$$は対数スケールです。
テキストのモデルに準拠いたしました。
モデルの内容を表示・可視化してみましょう。
### モデルの表示
model8【実行結果】

続いてモデルを可視化します。
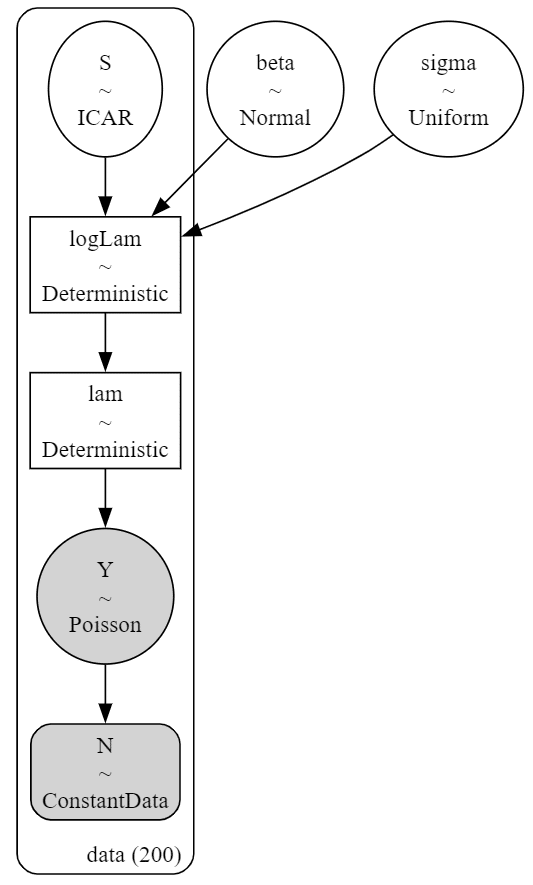
### モデルの可視化
pm.model_to_graphviz(model8)【実行結果】
前回の1次元のICARモデルと瓜二つ!
対数スケールの logLam($${\log \lambda}$$)を株数のスケールに変換した決定論的変数 lam($${\lambda}$$)を作りました。
lam($${\lambda}$$)は株数の期待値です。
MCMCサンプリングデータを後で活用します。
3. MCMCの実行と収束の確認
■ MCMC
マルコフ連鎖=chainsを4本、バーンイン期間=tuneを1000、利用するサンプル=drawを1chainあたり1000に設定して、合計4000個の事後分布からのサンプリングデータを生成します。テキストの指定数とは異なっています。
サンプル方法に numpyro を指定しています。処理速度が早くなります。
numpyro を使わない場合は「nuts_sampler='numpyro',」を削除します。
### 事後分布からのサンプリング 15秒
# NUTSの初期値を設定しなくても収束した
with model8:
idata8 = pm.sample(draws=1000, tune=1000, chains=4, random_seed=123,
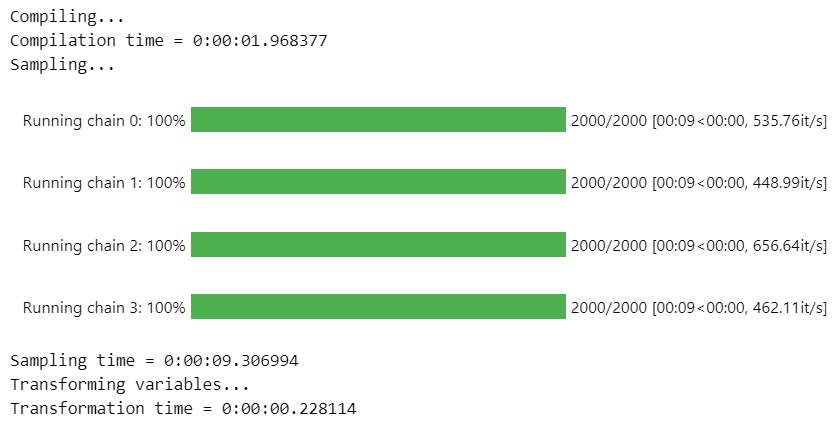
target_accept=0.9, nuts_sampler='numpyro')【実行結果】
処理時間は15秒です。
■ $${\hat{R}}$$で収束確認
収束の確認をします。
指標$${\hat{R}}$$(あーるはっと)の値が$${1.1}$$以下のとき、収束したこととします。
次のコードでは$${\hat{R}>1.01}$$のパラメータの個数をカウントします。
個数が0ならば、$${\hat{R} \leq1.1}$$なので収束したとみなします。
### r_hat>1.1の確認
# 設定
idata_in = idata8 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
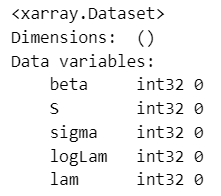
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R}>1.01}$$のパラメータは0個でした。
$${\hat{R} \leq1.1}$$なので収束したとみなします。
■ $${\hat{R}}$$の値把握と事後統計量の表示
### 事後統計量の表示
pm.summary(idata8, hdi_prob=0.95)【実行結果】
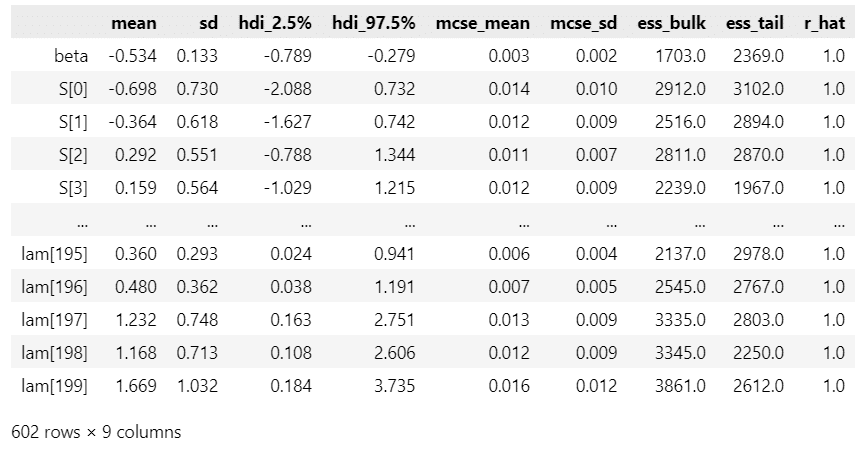
■ トレースプロットで収束確認
トレースプロットを描画します。
こちらの図でも収束の確認を行えます。
### トレースプロットの描画
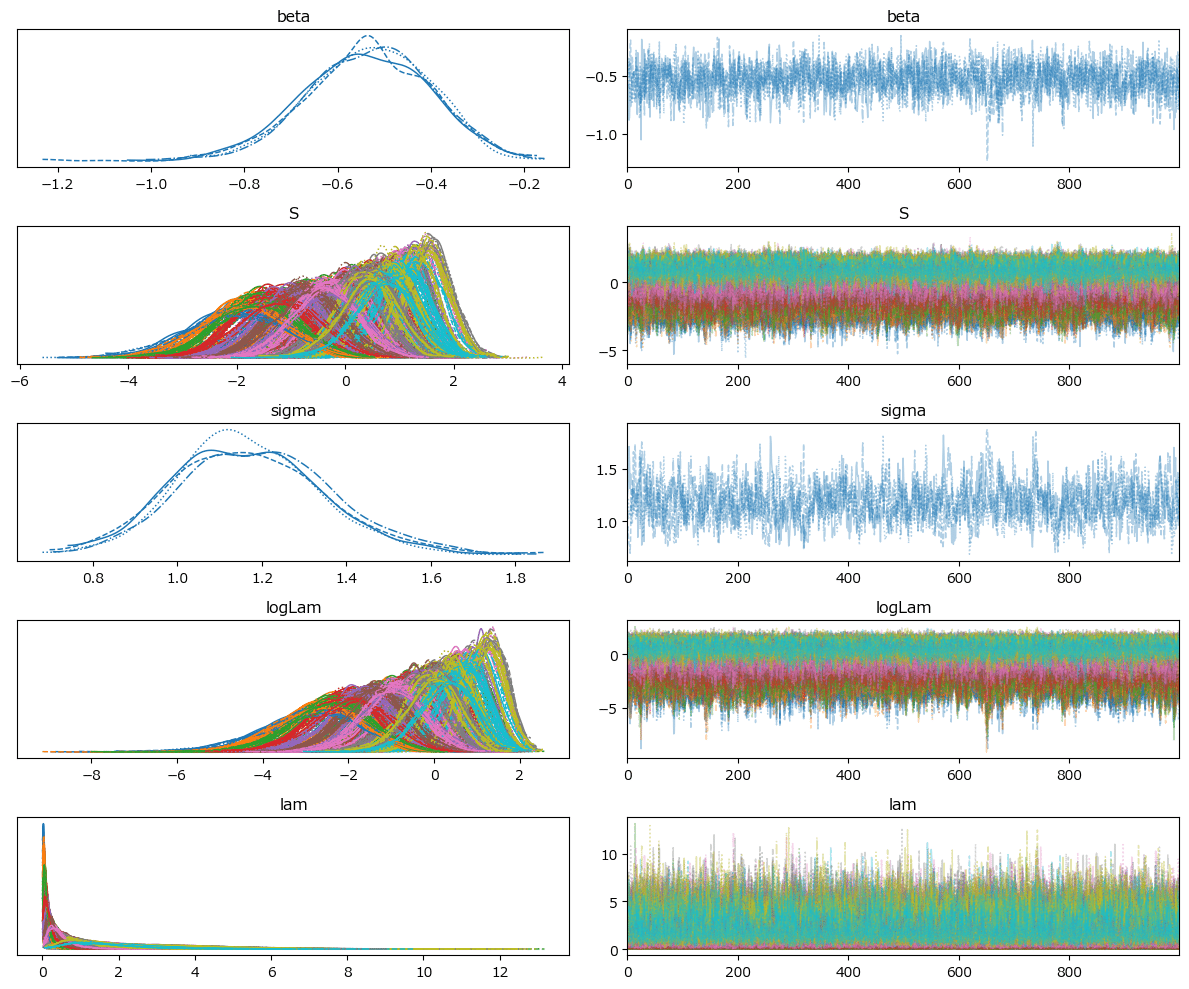
pm.plot_trace(idata8, compact=True)
plt.tight_layout();【実行結果】
左プロットの線の重なり具合、右プロットの偏りのない乱雑さより、収束している感じがします。
4. 分析
株数の期待値$${\lambda}$$の事後分布を用いてヒートマップを描画します。
テキストの図11に相当します。
### ヒートマップの描画 ※図11に相当
## 描画用データの作成
# λの事後平均の算出
lam_means = (idata8.posterior.lam.stack(sample=('chain', 'draw'))
.mean(axis=1).data)
# データフレーム化(data3のX軸・Y軸を利用したいので)
data3_add_lam = pd.concat([data3, pd.Series(lam_means, name='λ')], axis=1)
# 2次元化
lam_plot = data3_add_lam.pivot_table(index='Y', columns='X', values='λ')
## 描画
# 描画領域の指定
plt.figure(figsize=(10, 4))
# ヒートマップの描画
sns.heatmap(lam_plot, cmap='Greens', square=False, cbar_kws={'label': '株数'})
# 修飾
plt.title('京都市内の森林で観察されたアラカシの株数の分布\n'
'ICARによる期待値$\lambda$の予測値');【実行結果】
赤い線が$${\lambda}$$の事後分布の平均値、ピンクの面が$${\lambda}$$の95%HDI区間です。
青点の観測値は期待値$${\lambda}$$の95%HDIにだいたい収まっているようです。
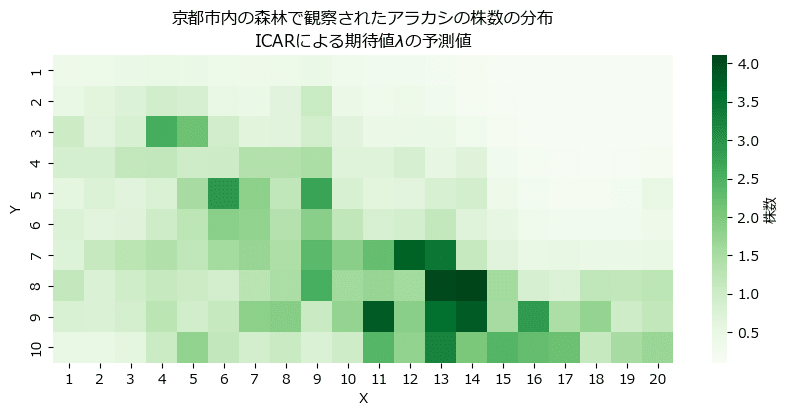
観測値のヒートマップと比べてみましょう。
テキストの通り「隣接する区間の間での値の変化がなめらかになっている」ことが分かります。
2次元のICARモデルのさらなる活用について、テキストは次のように語っています。
このモデルでは、ランダム効果と切片のみであてはめをおこないましたが、たとえば区画ごとの土壌の水分条件といった共変量を含めることももちろん可能です。そうすると、どのような環境条件が樹木の分布に影響を与えているのか、といったことを評価することもできるでしょう。
テキストで教わったシンプルなICARモデルを基礎にして、モデルに変数を追加して、モデルを育てる、というようなモデルのエコシステムができるといいですね!
2次元データの分析道具が1つ増えました。

5. 推論データの保存
pickle で MCMCサンプリングデータ idata8 を保存できます。
### 推論データの保存
file = r'idata8_ch3.pkl'
with open(file, 'wb') as f:
pickle.dump(idata8, f)次のコードで保存したファイルを読み込みできます。
### 推論データの読み込み
file = r'idata8_ch3.pkl'
with open(file, 'rb') as f:
idata8_ch3_load = pickle.load(f)ベイズ記事は以上です。

次回予告
「Stan入門」章
例題1「最小二乗法のベイズ版」
結び
最近のベイズ書籍写経を通じて、生態学分野で統計モデルが活用されていることが分かりました。
伊東先生はベイズモデリングを積極的に発信なさっておられます。
ブログには興味をそそるテーマが豊富に掲載されていました。
おわり
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
