8-5 正規近似を用いた検定 ～ 不良率を母比率に見立てて１標本の母比率のz検定を実施

今回の統計トピック

統計的仮説検定のトピック「１標本の母比率の$${z}$$検定」を深掘りします。
２回連続のトピックです。
（統計検定２級CBT問題集って母比率推しな気がする・・・）

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

日本統計学会公式認定　統計検定　2級　公式問題集［CBT対応版］

問題を解いて、知る・実践する

---

今回の記事の構成

この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」「知る」「実践する」を１つの章にまとめます。
１標本の母比率の$${z}$$検定の一連の流れを、手作業・EXCEL・Pythonで実践いたします。

📘公式問題集のカテゴリ

検定の分野
問5 正規近似を用いた検定（機械で製造する部品の不良率）

試験実施年月
統計検定2級 2018年11月 問15（回答番号25）

📕公式テキスト：4.3.4 母比率に関する検定（148ページ～）

問題

公式問題集をご参照ください。

解き方

題意
与えられた条件から１標本の母比率の検定を行って$${p}$$値を求めます。

【条件】
・標本サイズ：$${200}$$
・不良品数：$${16}$$
・母比率（不良品率）：$${r=0.08}$$
・帰無仮説：母比率$${r=0.05}$$
・対立仮説：母比率$${r>0.05}$$
・連続修正を行わない

公式問題集の記述を改変

読み解き

条件から統計的仮説検定の主題を読み解きます。

• 帰無仮説「母比率＝0.05」より、「１標本の母比率の検定」です。

• 対立仮説「母比率＞0.05」の不等号の向きより、「片側検定」で「上側確率」を利用します。

• 条件に明記されていませんが、標本サイズ$${200}$$が十分に大きいものとして扱われ、正規分布近似を用いた検定統計量$${Z}$$＆$${z}$$検定が想定されています。

この問題の統計的仮説検定の概要を図示します。

統計的仮説検定の手段

今回は、①手計算、②EXCEL、③Python の３つの手段で検定を実施いたします。

---

手計算で検定

ステップ１：検定統計量$${Z}$$を計算する

帰無仮説が正しいと仮定するときの検定統計量 $${Z}$$ を計算します。
計算結果の値を「$${z}$$値」と呼びます。
この問題で「帰無仮説が正しいと仮定する」とは、「母比率$${r=0.05}$$である」と仮定することです。

検定統計量$${Z}$$の計算式は次のとおりです。

■公式
検定統計量$${Z=\cfrac{\hat{r}-r_0}{\sqrt{r_0 (1-r_0)/n}}}$$

ただし、$${\hat{r}}$$：標本比率、$${r_0}$$：帰無仮説の母比率、$${n}$$：標本サイズ

問題文で与えられた$${\hat{r}=16/200=0.08}$$、$${r_0=0.05}$$、$${n=200}$$を用いて検定統計量$${Z}$$を計算します。

$$
\begin{align*}
z&=\cfrac{\hat{r}-r_0}{\sqrt{r_0 (1-r_0)/n}} \\
 \\
&=\cfrac{0.08-0.05}{\sqrt{0.05 \times (1-0.05)/200}} \\
 \\
&=\cfrac{0.03}{\sqrt{0.0002375}} \\
 \\
&=1.946 \cdots \\
&\fallingdotseq 1.95
\end{align*}
$$

$${z}$$値は$${1.95}$$です。

■ 検定統計量$${Z}$$の公式の補足
$${Z}$$の公式は「標本比率の標準化」の計算式です。
$${検定統計量Z = \cfrac{標本比率-母比率}{\sqrt{標本比率\times(1-標本比率)/標本サイズ}}}$$
※分母のルートの中の式は標本比率の分散です。
標本サイズが大きいとき、二項分布に関する中心極限定理によって、$${Z}$$は近似的に標準正規分布に従います。

ステップ２：$${\boldsymbol{z}}$$値から$${\boldsymbol{p}}$$値を取得

検定統計量$${Z}$$は標準正規分布に従います。
標準正規分布の上側確率表より、$${z}$$値の上側確率＝$${p}$$値を取得します。
これは確率$${P(Z \geq 1.95)}$$を求めることを意味します。

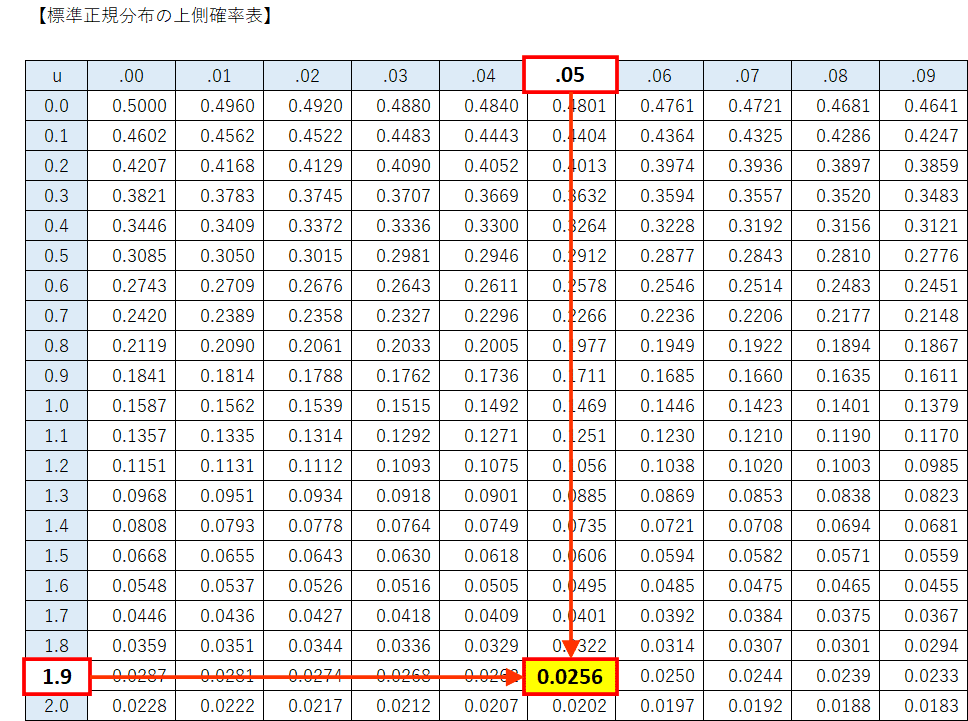
$${z}$$値$${1.95}$$の「1.9の行」・「.05の列」の交差点に求める上側確率が記載されています。
上側確率＝$${p}$$値は$${0.0256}$$です。

解答選択肢は$${0.026}$$です。

有意水準を$${5\%}$$として、統計的仮説検定を続けてみましょう。
$${p}$$値は$${0.026}$$であり$${5\%=0.05}$$よりも小さいので、有意水準$${5\%}$$で帰無仮説は棄却され、対立仮説「母比率$${r>0.05}$$」（不良率は5%より大きい）を採択します。

最後に、標準正規分布と$${z}$$値（横軸）、$${p}$$値（確率＝面積）の関係を可視化しましょう。

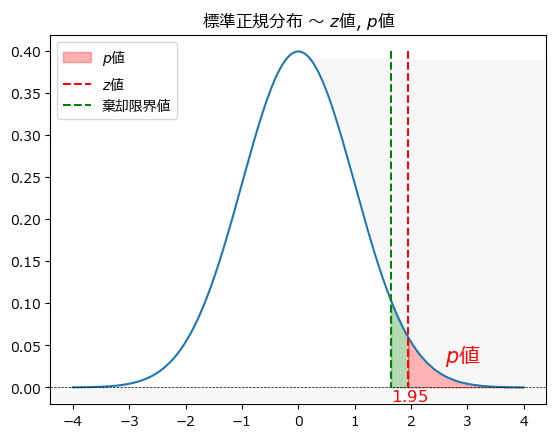
赤い点線を$${z}$$値の位置に立てています。
$${p}$$値は$${z}$$値より上側の赤い領域＝上側確率です。
また、上側確率$${5\%}$$点の$${1.645}$$が棄却限界値です。
緑の点線です。

棄却限界値と$${z}$$値を比較して、有意性を確認してみましょう。
有意水準を$${5\%}$$とする場合、棄却限界値（上側確率$${5\%}$$点）よりも$${z値}$$が大きいので、有意水準$${5\%}$$で帰無仮説は棄却されます。

手計算は以上となります。

---

EXCELで検定

EXCELで１標本の母比率の$${z}$$検定を行います。
記事「8-1 母平均の検定の考え方」で紹介した計算シートを活用いたします！

条件を入力パラメータに入力

入力パラメータに標本サイズ、標本比率、帰無仮説の母比率、有意水準、検定方法を設定します。

統計的仮説検定の実行

入力パラメータから$${z}$$値、$${p}$$値を自動計算します。

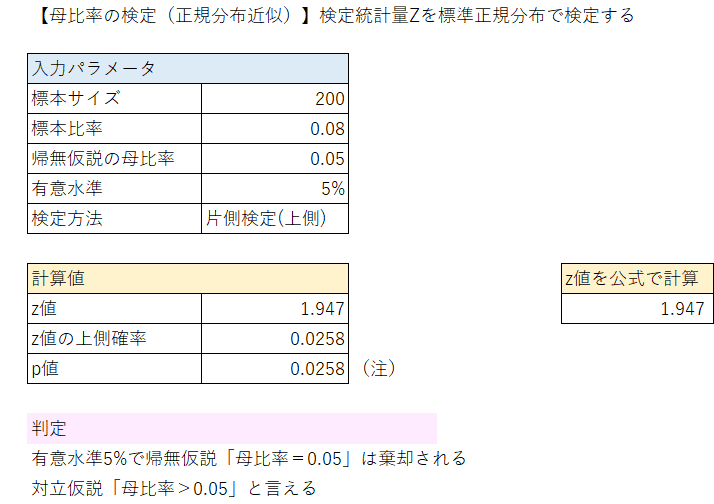
$${z}$$値$${=1.947}$$、$${p}$$値$${0.0258}$$になりました。

解答選択肢は$${0.026}$$です。

検定してみる

有意水準 5% で片側検定（上側）を行います。
$${p}$$値$${0.0258}$$が有意水準 5% を下回っているので、帰無仮説は棄却され、「不良品率は 0.05 より大きい」と言えます。

EXCELは以上となります。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

8-5_正規近似を用いた検定.xlsx

13.5 KB

ファイルダウンロードについて

ダウンロード

---

Pythonで検定

Pythonで１標本の母比率の$${z}$$検定を行います。
今回は、手組みのコードに取り組みます。

インポート

from scipy import stats
import numpy as np

$${\boldsymbol{z}}$$検定の実行

１標本の母比率の$${z}$$検定関数を定義します。
「# z値の計算」で検定統計量$${Z}$$公式通りに計算します。
「# p値の計算」では、正規分布 stats.norm で$${z}$$値の上側確率を取得して、両側検定・片側検定に即した$${p}$$値を計算します。

def z_test_1sample_proportion(sample_prop, sample_size, p0, alpha, H1='two-sided'):

    # 初期値設定
    test = {'two-sided': '両側検定', 'greater': '片側検定(>)', 'less': '片側検定(<)'}

    # z値の計算
    z = (sample_prop - p0) / np.sqrt((p0 * (1 - p0)) / sample_size)
    
    # p値の計算
    if H1=='two-sided': # 両側検定
        p_value = 2 * (stats.norm.sf(x=np.abs(z), loc=0, scale=1))
    elif H1=='greater':  # 片側検定、対立仮説:p>p0の場合
        p_value = stats.norm.sf(x=z, loc=0, scale=1)
    elif H1=='less': # 片側検定、対立仮説:p<p0の場合
        p_value = stats.norm.cdf(x=z, loc=0, scale=1)
    
    # 帰無仮説の棄却／受容の判定
    if alpha > p_value:
        result = '棄却'
    else:
        result = '受容'
    
    # 結果表示
    print(f'*** 母比率の検定の結果 ***\n'
          f'有意水準 {alpha:.1%} の{test[H1]}で 帰無仮説を {result}\n'
          f'z値:{z:.3f}, p値:{p_value:.4f}\n'
          f'母比率（帰無仮説）:{p0}, 標本比率:{sample_prop:.2f}, '
          f'標本サイズ:{sample_size}')

では、検定を実施しましょう。
問題集の条件を「設定」の各パラメータに設定します。
問題集で定めのない有意水準は 0.05 にしました。

### 母比率の検定：検定統計量Z

# 設定
#  標本比率:p_hat、標本サイズ：n、帰無仮説の母比率：p0、有意水準：alpha、
#  対立仮説：H1→ two-sided:p≠p0、greater:p>p0、less:p<p0
p_hat, n, p0, alpha, H1 = 16/200, 200, 0.05, 0.05, 'greater'

# 母平均の検定の実行、結果表示
z_test_1sample_proportion(p_hat, n, p0, alpha, H1)

$${z}$$値は$${1.947}$$、$${p}$$値は$${0.0258}$$、有意水準$${5\%}$$で帰無仮説は棄却され、「不良品率は 0.05 より大きい」と言えます。

$${p}$$値の解答選択肢は$${0.026}$$です。

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

8-5_正規近似を用いた検定.ipynb

50.3 KB

ファイルダウンロードについて

ダウンロード

以上で終了です。
お疲れ様でした。

THANK YOUのイラスト文字：「いらすとや」さんより

解答

② です。

難易度　やさしい

・知識：１標本の母比率の$${z}$$検定、標準正規分布の上側確率表
・計算力：数式組み立て（低）、電卓（低）
・時間目安：1分

---

おわりに

この問題は$${z}$$検定を選んでいます。
問題集の解説では「通常用いる検定統計量は$${Z}$$」としています。
しかし「通常」の判断基準がいまひとつ不明瞭です。
何かこう・・・、解答の際に判断に迷わない何か、が欲しいところです。
例えば、問題本文で「標本サイズが十分大きいことに言及する」とか、公式テキストで「標本サイズが◯◯以上の場合は十分大きいものとして扱ってよい」のような。

最後までお読みいただきまして、ありがとうございました。

---

のんびり統計シリーズの記事

次の記事

前の記事

目次