数学とPython 2 指数関数の曲線～グラフ・定積分・面積

ネイピア DS

2023年5月22日 11:48

はじめに

シリーズ数学とPythonのご案内

「シリーズ数学とPython」は、数学の学習中に「解けない、無理～」と焦ったときに、Pythonで数値の動きや可視化を行って、理解の糸口を見つけたときのことを記事にします。

データサイエンス数学ストラテジスト上級公式問題集

この記事は「データサイエンス数学ストラテジスト上級公式問題集」の問題の解読中に見つけたヒントを取り扱います。

今回取り組む問題

問題１３「曲線がつくる図形の面積は？」

Python実装

やりたいこと

問題集で与えられた指数関数の曲線$${y}$$に関する次の２点
・グラフ化
・定積分（曲線$${y}$$、直線$${x=1}$$、$${x}$$軸、$${y}$$軸が囲う領域の面積）

※指数関数の内容は、コード内の関数定義をご覧ください。

作戦

まず、曲線等を可視化して、囲う領域のイメージを掴みます。
その後、SciPyとSymPyを用いて定積分を実装します。

SciPyは数学、科学、工学分野のための数値解析ソフトウェア・ライブラリです（Wikipediaより）。

SymPyはPythonの代数計算ライブラリです。
「Python × 数学ブートキャンプ」でSymPyを学習しました。

実装の開始

インポート

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
from sympy import Symbol, exp, integrate, init_printing, simplify

描画
まず、曲線の形状を確かめます。

### まず、曲線の形状を確かめる
# 設定 グラフ描画区間
x_min, x_max = -9, 8

# 曲線の関数定義
def f(x):
    return 6 / ((np.exp(x)+1) * (np.exp(x)+3))

# 曲線の関数の値を取得してグラフを描画
x = np.linspace(x_min, x_max, 1001)
y = f(x)
plt.plot(x, y);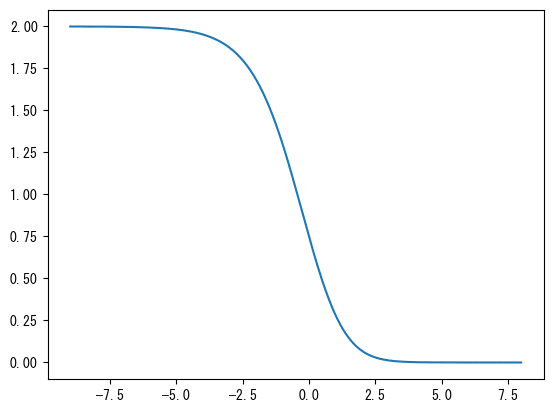

$${x}$$が -5 から 2.5 あたりの区間で $${y}$$の値が急勾配で減少しています。

次に、曲線等の囲う領域を描画します。

### x軸（y=0）,y軸（x=0）,x=1の直線を引いて面積を求める領域を可視化する
# 設定
x_min, x_max = -2, 3

# 曲線の関数の値を取得
x1 = np.linspace(x_min, x_max, 1001)
y1 = f(x1)

# 0≦x≦1の範囲の関数の値を取得
x2 = np.linspace(0, 1, 101)
y2 = f(x2)

# 描画
plt.plot(x1, y1)
plt.axvline(0, lw=0.5, ls='--', color='black')
plt.axhline(0, lw=0.5, ls='--', color='black')
plt.axvline(1, lw=0.5, ls='--', color='black')
plt.fill_between(x2, y2, 0, color='steelblue', alpha=0.1)
plt.show()

ブルーの領域の面積を積分で計算します。
台形に見立てて近似すると、（上底0.25+下底0.75）× 高さ 1 ÷ 2 = 0.5 くらいの領域です。

面積の計算

SymPyで定積分をします。
変数$${x}$$を定義して、被積分関数（曲線$${y}$$）をintegrand_f1に設定します。
integrate(integrand_f1, (x, 0, 1))で、積分区間$${[0,1]}$$の定積分を計算します。

### 定積分計算 by sympy.integrate
# 計算結果の数式を見やすくする
init_printing

# 積分変数xの定義
x = Symbol('x')

# 被積分関数の定義
integrand_f1 = 6 / ((exp(x)+1) * (exp(x)+3))
display(integrand_f1)

# 定積分の計算 (被積分関数, (積分変数,積分区間の下端, 上端)
integrate(integrand_f1, (x, 0, 1))

上段が今回取り組む指数関数の曲線$${y}$$です。

下段が定積分計算の結果です。
$${-\log(4)=-\log(2^2)=-2\log(2)}$$なので、$${-\log(4)}$$と$${3\log(2)}$$を整理して$${\log(2)}$$にしたいですね。

式の整理
SymPyのsimplifyで式を整理してみましょう。

simplify(integrate(integrand_f1, (x, 0, 1)))

確かに整理されました。
問題集の解答と異なる方向に着地しました。

面積の計算２

続いて、SciPyで定積分をします。
関数integrand_f2(x)に被積分関数（曲線$${y}$$）を定義します。
scipy.integrateのquadで数値積分を実行します。
引数は、quad( 関数, 積分区間の下端, 上端 ) です。
戻り値は、積分近似値と推定誤差です。

### 定積分計算 by scipy.integrate

# 被積分関数の定義
def integrand_f2(x):
    return 6 / ((np.exp(x)+1) * (np.exp(x)+3))

# 定積分の計算 (被積分関数, 積分区間の下端, 上端)
result, error = quad(integrand_f2, 0, 1)
print(result)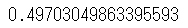

SciPyによる定積分計算の結果

計算結果は $${0.497 \cdots}$$です。
だいたい 5 です。

面積を求める領域を予めグラフで可視化して把握できたので、前もって計算結果の感覚を掴んでおくことができました。

可視化できてよかったです！
（数式と比べて優しい温もりを感じます😉）

【おまけ】

曲線$${y}$$のグラフを再掲します。
$${x}$$が$${-\infty}$$に近づくと$${y}$$は$${-2}$$に、$${x}$$が$${\infty}$$に近づくと$${y}$$は$${0}$$に、それぞれ収束するように見えます。

sympy の limit で極限を計算しましょう！
sympy では oo （小文字のo：オーを２文字）で無限大を表します。
無限大 oo のシンボルを infty に定義します。

# インポート、無限大の定義
from sympy import limit, oo
infty = oo

「面積の計算」で曲線$${y}$$を定義した「integrand_f1」を使います。
まず$${\displaystyle \lim_{x \to -\infty} y}$$から。

limit(integrand_f1, x, -infty)

出力イメージ

２に収束しました！

続いて$${\displaystyle \lim_{x \to \infty} y}$$。

limit(integrand_f1, x, infty)

出力イメージ

０に収束しました！

以上です。

おわりに

可視化して数式の気持ちに一歩でも近づくことが、数学理解の第一歩になりつつあります。
数式を見ただけでスッと頭に解答案が浮かぶようになるのがベストなのですが・・・（願望）

おわり

ブログの紹介

noteで３つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

３．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。