
第10章「オンライン調査における回答項目数のモデリング」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング」の第10章「オンライン調査における回答項目数のモデリング」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、回答の途中で中断可能なオンライン調査において、回答者が回答を打ち切る「ページ数・質問数」をベイズモデルで推論します。
注目点は強敵「幾何分布」が事前分布に仲間入りしたこと。
吉と出るか凶と出るか・・・。
今回もまたまた、自己流PyMCモデルはテキストと大きく異なる結果を出力しました(5回連続の汗)
結果はさておき、楽しくPyMCでモデリングして、ベイズ推論を満喫しましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 岡田謙介 先生
モデル難易度: ★★★・・ (ふつう)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ・・・・・& 測定不能 \\
結果再現度 & ・・・・・& 再現不能 \\
楽しさ & ★★★★・& 楽しそう \\
\end{array}
$$

評価ポイント
幾何分布の事前分布が騒動の種に!
今回のモデリングは「ほぼ棄権」レベルです。
実装精度と結果再現度ともに測定不能です。
工夫・喜び・反省
とある事象が原因となってテキストのモデルの実装を断念し、いくつかの代替案を試行錯誤しました。
3日ほどにわたる試行錯誤の過程を通じて、PyMCと仲良くなれた気がします。
モデルの概要
テキストの調査・実験の概要
■大規模オンライン調査「SAPAプロジェクト」
テキストでは、SAPAプロジェクトが実施したオンライン調査データ(23681人分)を利用します。
【SAPAプロジェクト】
【オンライン調査データの格納サイト】
テキストによると著者の興味は、オンライン調査データを利用して「参加者が回答する項目数のモデリング」を行うことです。
途中で回答を止める選択肢がある状況下で、全14ページ・322項目の質問のうち回答する項目数のメカニズムをベイズ推論を用いて調べる感じです。

テキストのモデリング
■目的変数と関心のあるパラメータ
目的変数$${y_i}$$は回答項目数です。
関心のあるパラメータは、①次ページに進まない確率$${\theta}$$、②教示に従って4ページ回答してやめる確率$${\omega}$$、③1問あたりの回答確率$${\psi_i}$$です。
テキストでは3つのモデルで分析していますが、この記事では「モデル3:回答するページ数の影響を表現できるよう改善したモデル」を試します。
■モデル
二項分布、幾何分布、ベルヌーイ分布など、離散型分布のオンパレードなのです!
$$
\begin{align*}
y_i &\sim \text{Binomial}\ (\psi_i, q_i) \\
\psi_i &= \cfrac{1}{1 + \exp\ (-(\beta_1 p_i + \beta_0))}\\
q_i &= \min(p_i,\ 4) \times 18 + \max\ ((p_i-4),\ 0) \times 25 \\
p_i &=
\begin{cases}
\alpha_i & (z_i=0\ and\ \alpha_i \leq14) \\
14 & (z_i=0\ and\ \alpha_1 > 14) \\
4 & (z_i=1)
\end{cases} \\
\alpha_i &\sim 1 + \text{Geometric}\ (\theta) \\
z_i &\sim \text{Bernoulli}\ (\omega) \\
\beta_0,\ \beta_1 &\sim \text{Cauchy}\ (1)\\
\theta &\sim \text{Uniform}\ (0,\ 1) \\
\omega &\sim \text{Uniform}\ (0,\ 1)
\end{align*}
$$
各変数の意味合いです。
$${q_i}$$は参加者$${i}$$にオンラインで提示される回答項目数
$${p_i}$$は参加者$${i}$$が回答するページ数
$${\alpha_i}$$は参加者$${i}$$回答すると想定されるページ数(ただし、上限14ページの打ち切りを未考慮)
$${z_i}$$は参加者$${i}$$が「教示」に従って4ページに回答してやめる参加者である場合1,違う場合0。参加者には教示「少なくとも4ページまでは回答する」が与えられていました
$${\omega}$$は参加者が教示に従う群に属する確率
$${\psi_i}$$は参加者$${i}$$の提示された回答項目数に対する回答確率
$${\theta}$$はあるページまで回答した時点で回答をやめる確率
事前分布に「離散型分布」である幾何分布$${\text{Geometric}}$$とベルヌーイ分布$${\text{Bernoulli}}$$が含まれています。
Stanは離散型分布を扱えないそうで、テキストでは「JAGS」を用いて実装しています。
■分析・分析結果
分析結果はテキストに記載の図表を利用して実施して下さい。
PyMCの自己流モデルはテキストと異なる結果になり、分布は収束せず、分析に利用してはいけない状況です(スミマセン・・・)。

PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.データのダウンロード
次のサイトにアクセスして「sapaTempData696items08dec2013thru26jul2014.tab」ファイルをカンマ区切り:Comma Separated Values(Original File Format)」でダウンロードします。
【ダウンロードサイト】
2.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')3.データの読み込みと前処理
ダウンロードしたファイルをpandasのデータフレームに読み込みます。
続いて、データの前処理を行い、データセット obs を作成します。
### データの読み込みと前処理
# データの読み込み
data = pd.read_csv('sapaTempData696items08dec2013thru26jul2014.csv')
print('original data shape: ', data.shape)
# q_で始まる回答列だけに絞り込み
col_tmp = data.columns
col_qa = [s for s in col_tmp if s.startswith('q_')]
data = data[col_qa]
print('answer data shape : ', data.shape)
# すべての値が欠損値の行を削除(一切回答しない人1件)
data = data.dropna(how='all', axis=0).reset_index(drop=True)
print('final data shape : ', data.shape)
display(data.head())
# 観測データの作成:回答者ごとの回答数
obs = data.count(axis=1)
print('observed data shape: ',obs.shape)
print(obs[:10])【実行結果】
obs は、インデックスが回答者ID、値が目的変数である「回答項目数」で構成されます。

3.データの外観・統計量
ひとまず要約統計量を確認します。
### 要約統計量の表示
obs.describe().to_frame().rename(columns={0: '回答項目数'}).round(2)【実行結果】
平均値が第三四分位数よりも大きいです。

ヒストグラムを描画しましょう。
### ヒストグラムの描画
plt.figure(figsize=(8, 3))
plt.hist(obs, bins=322)
plt.xlabel('回答項目数')
plt.ylabel('度数:回答者数');【実行結果】
70前後に集中しています。
300付近にも峰が見られます。


モデル構築
テキストの「10.4 モデル3:回答するページ数の影響を表現できるよう改善したモデル」のモデルです。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
目的変数$${y_{data}}$$の添字$${data}$$はデータのインデックスであり、$${data = 0, \cdots, 5}$$です。
$$
\begin{align*}
\theta &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1) \\
\omega &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=1) \\
\beta_0 &\sim \text{Cauchy}\ (\text{alpha}=0,\ \text{beta}=1) \\
\beta_1 &\sim \text{Cauchy}\ (\text{alpha}=0,\ \text{beta}=1) \\
\alpha_{tmp} &\sim \text{Geometric}\ (\text{p}=\theta) \\
\alpha_i &= 1 + \alpha_{tmp} \\
z_i &\sim \text{Bernoulli}\ (\text{p}=\omega) \\
p_i &= \text{switch}(z_i = 1, 4, \text{switch}(\alpha_i \leq 14, \alpha_i, 14))\\
q_i &= \text{switch}(p_i \leq 4, p_i, 4) \times 18 + \text{switch}(p_i-4 \geq 0, p_i-4, 0) \times 25\\
\psi_i &= \text{invlogit}\ (\beta_1 \times p_i + \beta_0)\\
likelihood &\sim \text{Binomial}\ (\text{n}=q_i,\ \text{p}=\psi_i) \\
\end{align*}
$$
1.モデルの定義
事前分布に離散型分布を含んだモデルを定義します。
### モデルの定義
with pm.Model() as model3:
### データ関連定義
# coordの定義
model3.add_coord('data', values=obs.index, mutable=True)
# dataの定義
y = pm.Data('y', value=obs.values, dims='data', mutable=True)
### 事前分布
# 事前分布
theta = pm.Uniform('theta', lower=0, upper=1)
omega = pm.Uniform('omega', lower=0, upper=1)
beta0 = pm.Cauchy('beta0', alpha=0, beta=1)
beta1 = pm.Cauchy('beta1', alpha=0, beta=1)
# 回答するページ数p、alpha:打ち切り幾何分布
alphaTmp = pm.Geometric('alphaTmp', p=theta, dims='data')
alpha = pm.Deterministic('alpha', 1 + alphaTmp, dims='data')
z = pm.Bernoulli('z', p=omega, dims='data')
p = pm.Deterministic('p',
pt.switch(pt.eq(z, 1), 4, pt.switch(pt.le(alpha, 14), alpha, 14)),
dims='data')
# 質問項目数q
q = pm.Deterministic('q',
pt.switch(pt.le(p, 4), p, 4)*18 + pt.switch(pt.ge(p-4, 0), p-4, 0)*25,
dims='data')
# 回答確率psi
psi = pm.Deterministic('psi', pm.invlogit(beta1*p + beta0), dims='data')
### 尤度 0<p<1
likelohood = pm.Binomial('likelihood', n=q, p=psi, observed=y, dims='data')【モデル注釈】省略
2.モデルの外観の確認
### モデルの表示
model3【実行結果】
複雑な感じがします。

# モデルの可視化
pm.model_to_graphviz(model3)【実行結果】
縦長です。

3.事後分布からのサンプリング
乱数生成数(draws, tune)はテキストと同様です。
事前分布に離散型分布を含んでいる場合、numpyroをNUTSサンプラーに指定することができません。
そこでPyMC標準のサンプラーを利用することにします。
### 事後分布からのサンプリング
with model3:
idata3 = pm.sample(draws=4000, tune=1000, chains=3, target_accept=0.9,
random_seed=123)【実行結果】
エラーが発生しました。
初期値が良くないようです。

SamplingError: Initial evaluation of model at starting point failed! Starting values: {'theta_interval__': array(0.), 'omega_interval__': array(0.), 'beta0': array(0.), 'beta1': array(0.), 'alphaTmp': array([2, 2, 2, ..., 2, 2, 2], dtype=int64), 'z': array([1, 1, 1, ..., 1, 1, 1], dtype=int64)} Logp initial evaluation results: {'theta': -1.39, 'omega': -1.39, 'beta0': -1.14, 'beta1': -1.14, 'alphaTmp': -32824.68, 'z': -16412.34, 'likelihood': -inf} You can call `model.debug()` for more details.
4.事後分布からのサンプリング その2
初期値を設定してみます。
エラーメッセージに表示された「Starting values」の辞書をコピペして、適当な値を試行錯誤で書き換えてinit_valsを作成しました。
pm.sample()の引数 initvalで初期値を指定します。
### 事後分布からのサンプリング
init_vals = {'theta_interval__': np.array(0.1),
'omega_interval__': np.array(0.1),
'beta0': np.array(0.1),
'beta1': np.array(0.1),
'alphaTmp': np.zeros(len(obs), dtype='int64') + 100,
'z': np.zeros(len(obs), dtype='int64') }
with model3:
idata3 = pm.sample(draws=4000, tune=1000, chains=3, target_accept=0.9,
initvals=init_vals, random_seed=123)【実行結果】
無事にエラー発生を回避することができました。
がしかし…
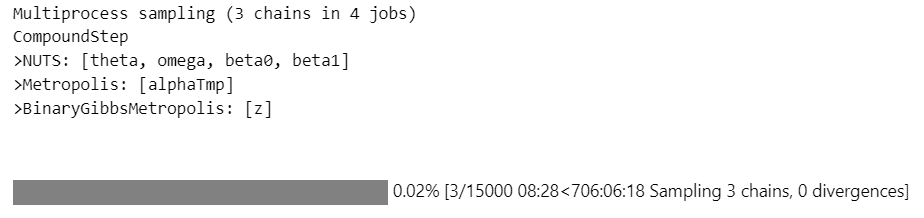
プログレスバー(進捗バー)の残り時間の予測値は…
「706:06:18」
706時間6分18秒!およそ30日!約1か月!!!
断念するしか無いです(泣)

5.代替モデルの検討
Stan周りの情報を調べると、離散型分布を扱えないStanのために、離散型分布を連続型分布に変換するテクニック情報が見つかります。
しかし、私にとって手の届かない、超高度なテクニックであり、手を出すことができません。
したがって、別の方法を考えました。
かなり適当(てきとー)にモデルを描きました。
「幾何分布→ワイブル分布」、「ベルヌーイ分布→一様分布」という、脈絡のない変換です(泣)
ただし、NUTSサンプラーに numpyro を使えるので、MCMC処理時間は短縮できるはずです!
### モデルの定義
# モデルの定義
with pm.Model() as model3m:
### データ関連定義
# coordの定義
model3m.add_coord('data', values=obs.index, mutable=True)
model3m.add_coord('nextpage', values=np.arange(13), mutable=True)
# dataの定義
y = pm.Data('y', value=obs.values, dims='data', mutable=True)
### 事前分布
# 事前分布
omega = pm.Uniform('omega', lower=0, upper=1)
a = pm.Uniform('a', lower=0, upper=14)
b = pm.Uniform('b', lower=0, upper=14)
beta0 = pm.Cauchy('beta0', alpha=0, beta=1)
beta1 = pm.Cauchy('beta1', alpha=0, beta=1)
# 回答するページ数p
alphaTmp = pm.Weibull('alphaTmp', alpha=a, beta=b, dims='data')
alpha = 1 + pt.floor(alphaTmp)
z = pm.Uniform('z', lower=0, upper=1, dims='data')
p = pm.Deterministic('p', pt.switch(pt.gt(z, 1 - omega), 4,
pt.switch(pt.le(1 + pt.floor(alpha), 14), alpha, 14)),
dims='data')
# 質問項目数q
q = pm.Deterministic('q',
pt.switch(pt.le(p, 4), p, 4)*18 + pt.switch(pt.ge(p-4, 0), p-4, 0)*25,
dims='data')
# 回答確率psi
psi = pm.Deterministic('psi', pm.invlogit(beta1*p + beta0), dims='data')
### 尤度
likelohood = pm.Binomial('likelihood', n=q, p=psi, observed=y, dims='data')モデルの外観確認です。
### モデルの表示
model3m【実行結果】

# モデルの可視化
pm.model_to_graphviz(model3m)【実行結果】

事後分布からのサンプリングを実行します。
NUTSサンプラーに numpyro を用いて、5分30秒程度かかりました。
なお、処理途中で「メモリ不足」が発生して処理中断になる場合があります。
メモリ不足の対処として、サンプリング個数(draws$${\times}$$chains)をテキストよりも減らしています。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを未使用 5分30秒
with model3m:
idata3m = pm.sample(draws=2500, tune=1000, chains=4, target_accept=0.95,
nuts_sampler='numpyro', random_seed=123)6.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
### r_hat>1.1の確認
rhat_idata3m = az.rhat(idata3m)
(rhat_idata3m > 1.1).sum()【実行結果】
全てのパラメータが$${\hat{R} \geq1.1}$$となりました。
つまり、全然収束していません!

ひとまずトレースプロットを確認します。
### トレースプロットの表示
var_names = ['omega', 'a', 'b', 'beta0', 'beta1']
pm.plot_trace(idata3m, var_names=var_names, combined=True, figsize=(12, 10))
plt.tight_layout();【実行結果】
4つのチェーンごとに異なる分布が描かれたように見えます。

分布の収束を果たせなかったので、分析を断念することにします。

以降はコード参考例の位置づけでご覧ください。
7.事後予測を用いた確認
事後予測をサンプリングを行って、目的変数の予測値を取得してみましょう。
### 事後予測のサンプリング
with model3m:
idata3m.extend(pm.sample_posterior_predictive(idata3m))【実行結果】

目的変数である「回答項目数」の観測値 obs と予測値、そして、モデルの途中で計算される質問数 q をヒストグラムで比較してみます。
### 回答項目数の観測値obs・予測値post predと途中計算値qの比較
plt.hist(obs, density=True, bins=30, histtype='stepfilled', alpha=0.5,
label='obs')
plt.hist(idata3m.posterior.q.data.flatten(), bins=30, density=True,
histtype='step', label='q')
plt.hist(idata3m.posterior_predictive.likelihood.data.flatten(), density=True,
bins=30, histtype='stepfilled', alpha=0.5, label='post pred')
plt.legend();【実行結果】
目的変数の予測値 post pred よりも、途中計算値の q のほうが観測値に近い感じがします。
$${\psi_i}$$の推定がうまくいっていないようです。

以上で第10章は終了です。
おわりに
周辺化消去
離散パラメータを含むモデルへの対処方法の1つに周辺化消去というものがあるそうです。離散パラメータを消してしまうのです。
PyMCでは、pymc_experimentalの「MarginalModel」で「周辺化」を行えるようです。
pymc_experimental公式サイトのコードをお借りして、試してみます。
### インポート
import pymc as pm
from pymc_experimental import MarginalModel
### モデルの定義とMCMCの実行
with MarginalModel() as m:
# 事前分布:変数zはベルヌーイ分布に従う
p = pm.Beta('p', alpha=1, beta=1)
x = pm.Bernoulli('x', p=p, shape=(3,))
# 尤度
y = pm.Normal('y', mu=pm.math.switch(x, -10, 10), observed=[10, 10, -10])
# 周辺化
m.marginalize([x])
# MCMC
idata_m = pm.sample(nuts_sampler='numpyro', random_seed=1234)変数 x は離散型分布であるベルヌーイ分布に従います。
周辺化「marginalize([x])」とすることで x の存在が消えてしまいます。
また、NUTSサンプラーにnumpyroを利用できます!
### モデルの可視化
pm.model_to_graphviz(m)【実行結果】
変数 x が見当たりません。消去されたようです。

### 推論データの要約統計情報の表示
pm.summary(idata_m)【実行結果】
$${hat{R}}=1.0$$であり、収束しているようです。

### トレースプロットの表示
pm.plot_trace(idata_m, combined=True);【実行結果】

ただし、いくつかの制約があります。
MCMCでサンプリングデータを取得したい離散パラメータを周辺化すると、サンプリング対象から外れるので(消えてしまうので)、サンプリングデータを得られなくなります。
対応できる離散型分布が次の3つに限定されています。
Bernoulli
Categorical
DiscreteUniform
周辺化する離散パラメータを使う決定論的変数を「Deterministic」で定義できません。従って、離散パラメータと同様に決定論的変数の値もサンプリングデータを得られなくなります。
例えば x が離散パラメータのとき、「w = pm.Deterministic('w', x**2)」とすると、エラーになります。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ(お題)を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます!
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。
最後までお読みいただきまして、ありがとうございました。
