実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で⑨空間自己回帰モデル：1次元の個体数カウントデータ

2024年3月27日 11:29

「時系列・空間データのモデリング」章

テキスト「時系列・空間データのモデリング」の執筆者
伊東宏樹先生

この記事は、テキストの「時系列・空間データのモデリング」章の「1次元の個体数カウントデータを用いた空間自己回帰モデル」の実践を取り扱います。
空間的に自己相関のある1次元データに対して、条件付き自己回帰モデル（Intrinsic CARモデル）を用いた推論を行います。
たのしくPyMCモデリングを進めましょう！

この章を執筆された伊東先生は「たのしいベイズモデリング２」第５章を執筆されています。
樹木の直径と高さの数理モデルをベイズに取り込んでいます！
こちらもお楽しみくださいませ。

（ご参考）書籍「たのしいベイズモデリング２」

（ご参考）たのしいベイズモデリング２のPyMC化ブログ

はじめに

岩波データサイエンスVol.1の紹介

この記事は書籍「岩波データサイエンス vol.1」（岩波書店、以下「テキスト」と呼びます）の特集記事「ベイズ推論とMCMCのフリーソフト」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。

テキストは、2015年10月に発売され、ベイズモデリングの様々なソフトウェアを用いたモデリング事例を多数掲載し、ベイズモデリングの楽しさを紹介する素晴らしい書籍です。
入門的なモデルから2次階差を取り扱う空間モデルまで、幅広い難易度のモデルを満喫できます！

このシリーズは、テキストのベイズモデルをPyMC Ver.5に書き換えて実践します。

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「岩波データサイエンス vol.1」
第９刷、編者岩波データサイエンス刊行委員会　岩波書店

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

PyMC環境の準備

Anacondaを用いる環境構築とGoogle ColaboratoryでPyMCを動かす方法について、次の記事にまとめています。
「PyMCを動かすまでの準備」章をご覧ください。

PythonとPyMC
テキストで利用するツールは、R、BUGS、JAGS 等です。
この記事では、PythonとPyMCを用いたコードに変換してベイズモデリングを実践いたします。

イントロ

1. モデルのイメージ

■ 空間データの自己相関
1次元の空間の自己相関、なんだか難しい言葉が並んでいます。
イメージ的には、１列に並んだデータがあって、各データ点は前後のお隣さんの影響を受ける、みたいな感じだと思います。

時間の場合、時系列データ（1次元）は「過去の時間の影響」を受けている＝自己相関がある、という関係性がありました。
空間の場合にも、空間データ（1次元）は「場所的に前後の空間の影響」を受けている＝自己相関がある、という感じです。

■ Intrinsic CAR モデル
テキストの説明を引用いたします。

Intrinsic CAR（Conditional Auto-Regressive; 条件付き自己回帰）モデルは空間自己相関を扱うモデルのひとつで、場所ごとのランダム効果が近隣のデータに依存して決まると考えます。
すなわち、場所$${i=1, 2, \cdots, n}$$のランダム効果を$${S=(S_1, S_2, \cdots, S_n)}$$とするとき、$${S_i}$$は$${i}$$以外の$${S\ =(S_{-i})}$$に依存して決まるとして、以下の式で与えられます。

$$
S_i \mid S_{-i} \sim \text{Normal}\ \left( \displaystyle \sum_{j \neq i} \cfrac{w_{ij}S_j}{w_{i+}},\ \cfrac{\sigma^2}{w_{i+}} \right)
$$

テキストより引用

モデリングを先取りすると、重みづけ変数$${w_{ij}}$$は、場所$${i}$$と場所$${j}$$が隣り合っている場合は１、その他の場合は０と設定されます。
この設定方法の場合、数式の分母$${w_{i+}}$$は「場所$${i}$$と隣り合う場所の数」になります。
重みづけ変数$${w_{ij}}$$がモデルの肝のようですね！
重みづけ変数を決めて定数化すると、隣り合う場所の数も定数になります。

数式の右辺は、「近隣のランダム効果の平均」と「近隣数に反比例する分散」がパラメータの正規分布、ということが見えてきました。
重みでお隣さんを大切にするモデル、なんですね。

重みとお隣さんに注目して、次に進みましょう。

2. インポート

「時系列・空間データのモデリング」章で利用するパッケージをインポートします。

### インポート

# ユーティリティ
import pickle

# 数値・確率計算
import pandas as pd
import numpy as np

# 確率統計
import statsmodels.formula.api as smf

# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az

# WEBアクセス
import requests

# Rdata読み込み
import pyreadr

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

3. データの読み込み

久保拓弥先生の「データ解析のための統計モデリング入門」（通称、緑本）第11章のデータをお借りします。

久保先生のWebサイトからCSVファイルをダウンロードして、pandasのデータフレームに読み込みます。
テキスト掲載のURLから変わっていますのでご注意ください。
まずは、ダウンロードしてPCに保存します。
「# 設定：ダウンロードファイルの格納先パス＋ファイル名」の箇所で、適宜、フォルダ名とファイル名を指定してください。

### データのダウンロード

# 設定：ダウンロードファイルの格納先パス＋ファイル名
filename = r'./data/Y.RData'

# ダウンロードの実行
url = r'https://kuboweb.github.io/-kubo/stat/iwanamibook/fig/spatial/Y.RData'
res = requests.get(url)
with open(filename, mode='wb') as f:
  f.write(res.content)

【実行結果】なし

続いて、データの読み込みです。
R 特有のデータ形式を取り扱える pyreadr を利用します。

### データの読み込み

# pyreadrでRDataファイルを読み込み（collections.OrderedDict型）
data2 = pyreadr.read_r(filename)
# 列Yを取り出し（pandasデータフレーム）
data2 = pd.DataFrame({'X': list(range(1, 51)),
                      'Y': data2['Y'].values.squeeze()})
# データの表示
print('data2.shape: ', data2.shape)
display(data2.head())

【実行結果】
１次元上に等間隔で並ぶ50個の調査地 X でカウントしたある植物の個体数 Y です。

4. データの外観の確認

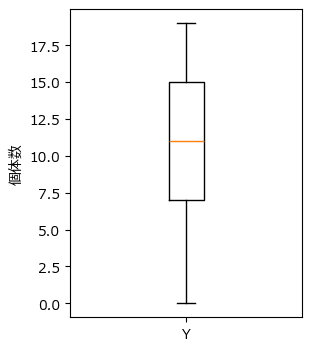
箱ひげ図で各場所の個体数のばらつきを見てみましょう。

### 箱ひげ図の描画
plt.figure(figsize=(3, 4))
plt.boxplot(data2.Y)
plt.xticks(ticks=[1], labels=['Y'])
plt.ylabel('個体数');

【実行結果】
平均約10個、0個～18個くらいまでの範囲、四分位範囲は7.5～15個、のようです。

5. 一般化線形混合モデル

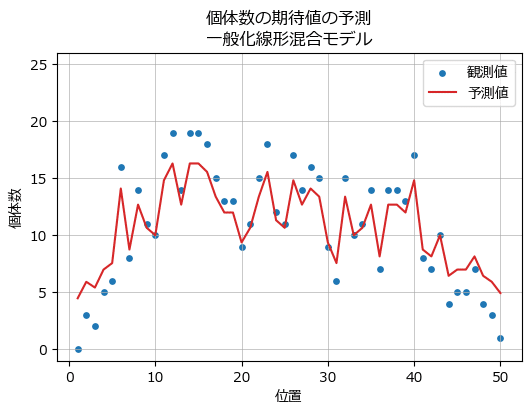
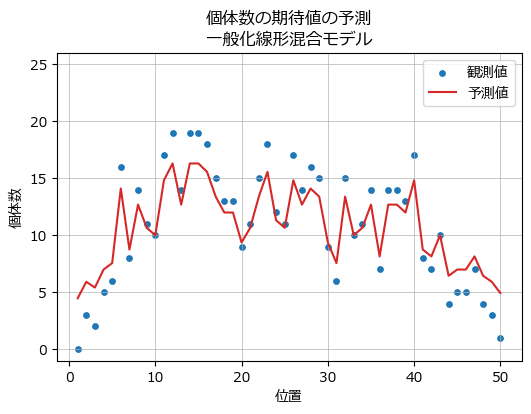
テキストの図7では、空間構造を考慮せず、調査地ごとのランダム効果と切片からなる一般化線形混合モデル（GLMM）の予測個体数をプロットしています。
一般化線形混合モデルで予測して、グラフにしてみましょう。
一般化線形混合モデリングには「GPBoost」を利用します。

GPBoostのインストールは pip で行います。

pip install gpboost -U

ランダム効果を group_data で設定する点や、切片 1 の設定方法に patsy の dmatrix を利用する点（もっといい方法があるかもしれません…）など、少々ややこしい点がありますが、次のコードで一般化線形混合モデル（ポアソン分布）の分析ができました。

### 一般化線形混合モデル formula的には 'Y ~ 1 + (1|X)' です。

# インポート
import gpboost as gpb
from patsy import dmatrix

# 変数の定義
X = dmatrix('1', data=data2)
y = data2.Y
group = data2.X

# gpboostのモデル定義
model_gp = gpb.GPModel(group_data=group, likelihood='poisson')

# フィッティングと結果表示
model_gp.fit(X=X, y=y)
print(model_gp.summary())

【実行結果】

フィッティング後のモデル model_gp から、切片を get_coef()で、ランダム効果を predict_training_data_random_effects() で取り出して、描画します。
取り出した値は対数スケールなので、np.exp()で個体数のスケールに変換します。

### 観測値とGLMMによる予測値を描画 ※図7に相当

# 切片とランダム効果との取り出し
intercept = model_gp.get_coef().iloc[0, 0]
random_effects = model_gp.predict_training_data_random_effects()
# 描画領域の指定
plt.figure(figsize=(6, 4))
ax = plt.subplot()
# 観測値の散布図の描画
ax.scatter(data2.X, data2.Y, s=15, color='tab:blue', label='観測値')
# 切片＋ランダム効果の折れ線グラフの描画
ax.plot(data2.X, np.exp(intercept + random_effects),
        color='tab:red', label='予測値')
# 修飾
ax.set(ylim=(-1, 26), xlabel='位置', ylabel='個体数',
       title='個体数の期待値の予測\n一般化線形混合モデル')
ax.legend()
ax.grid(lw=0.5)
plt.show()

【実行結果】
一般化線形混合モデルの予測は中々良さげに見えるのは私だけでしょうか？
ベイズICARモデルの予測がますます楽しみになりました！

では、PyMCモデリングに進みます。

ベイズモデル～ ICARモデル

1. モデル数式

テキストのGeoBUGSコードとPyMC公式サイトの情報を参考にしてPyMCモデルを作成しました。
このPyMCモデルから逆引きして数式を書いてみました。

$$
\begin{align*}
\beta &\sim \text{Normal}\ (\text{mu}=0,\ \text{sigma}=100)\\
\sigma &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
S &\sim \text{ICAR}\ (\text{w}=w,\ \text{sigma}=1) \\
\log \lambda &= \beta + S \sigma \\
Y &\sim \text{Poisson}\ (\text{mu}=\lambda) \\
\end{align*}
$$

2. モデルの定義

まず最初に重みづけデータを作成します。
テキストでは「隣接行列」と呼んでいます。
PyMCでは ICARクラスの引数 w に隣接行列を指定します。

### 隣接行列Wの作成
W = np.zeros((len(data2), len(data2)))
for i in range(1, len(data2)):
    W[i, i-1] = W[i-1, i] = 1
print('W.shape: ', W.shape)
print(W)

【実行結果】
調査地50点×50点のマトリクスになりました。

■ 見方
行を起点地（$${i}$$）、列をお隣さん判定（$${j}$$）と見立てます。
１行目は調査地１です。お隣さんは値「１」が立っている列２＝調査地２です。
２行目は調査地２です。お隣さんは値「１」が立っている調査地１と調査地３です。

PyMCのモデルを定義しましょう。
Intrinsic CAR モデルは ICAR クラスで実装します。

### モデルの定義
with pm.Model() as model6:

    ### データ関連定義
    # coordの定義
    model6.add_coord('data', values=data2.index, mutable=True)
    # dataの定義
    y = pm.ConstantData('y', value=data2.Y.values, dims='data')

    ### 事前分布
    # 切片
    beta = pm.Normal('beta', mu=0, sigma=100)
    # 標準偏差
    sigma = pm.Uniform('sigma', lower=0, upper=100)
    
    ### 切片β＋空間構造を取り入れたランダム効果Sのモデル
    # 非中心配置のパラメータ化：ICARの標準偏差を1にして、結果のSにsigmaを乗ずる
    S = pm.ICAR('S', W=W, sigma=1, dims='data')
    logLam = pm.Deterministic('logLam', beta + S*sigma, dims='data')

    ### 尤度：ポアソン分布
    lam = pm.Deterministic('lam', pt.exp(logLam), dims='data')
    Y = pm.Poisson('Y', mu=lam, observed=y, dims='data')

■ モデルの注釈
ランダム効果$${S}$$には pm.ICAR() クラスを用いました。
PyMC公式サイトによる「標準偏差の設定」の仕方について補足します。
確率分布 ICAR の標準偏差$${\sigma}$$を ICAR の標準偏差 sigma 引数に設定せず、次のように分離して設定する「非中心配置のパラメータ化」です。

pm.ICAR() では標準偏差に１を設定する。
pm.ICAR() の結果変数である$${S}$$を次式の logLam で使用する際、$${S}$$に標準偏差$${\sigma}$$を乗じます。

また、$${\beta}$$と$${S,\ \sigma}$$は対数スケールです。
テキストのモデルに準拠いたしました。

モデルの内容を表示・可視化してみましょう。

### モデルの表示
model6

【実行結果】

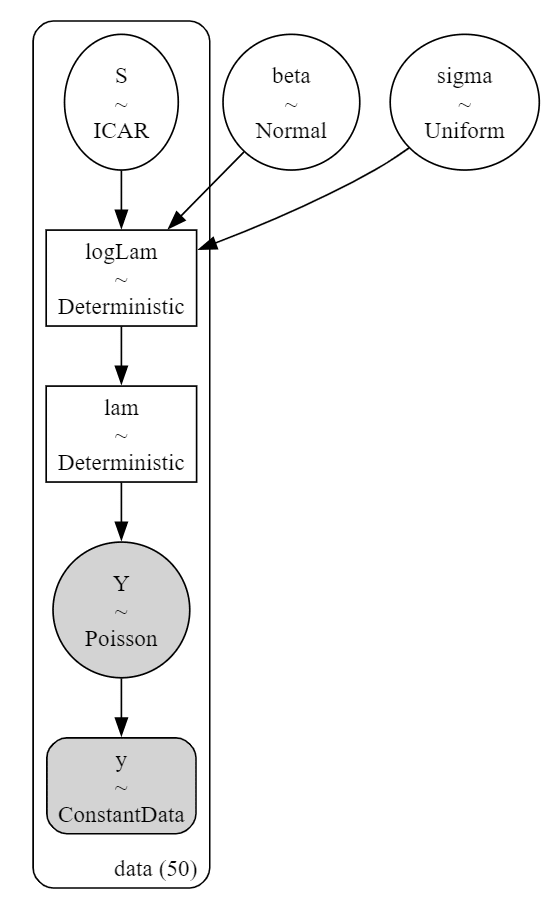
続いてモデルを可視化します。

### モデルの可視化
pm.model_to_graphviz(model6)

【実行結果】

対数スケールの logLam（$${\log \lambda}$$）を個体数のスケールに変換した決定論的変数 lam（$${\lambda}$$）を作りました。
lam（$${\lambda}$$）は個体数の期待値です。
MCMCサンプリングデータを後で活用します。

3. MCMCの実行と収束の確認

■ MCMC
マルコフ連鎖=chainsを4本、バーンイン期間=tuneを1000、利用するサンプル=drawを１chainあたり1000に設定して、合計4000個の事後分布からのサンプリングデータを生成します。テキストの指定数とは異なっています。
サンプル方法に numpyro を指定しています。処理速度が早くなります。
numpyro を使わない場合は「nuts_sampler='numpyro',」を削除します。

### 事後分布からのサンプリング 15秒
# NUTSの初期値を設定しなくても収束した
with model6:
    idata6 = pm.sample(draws=1000, tune=1000, chains=4, random_seed=123,
                       target_accept=0.85, nuts_sampler='numpyro')

【実行結果】
処理時間は15秒です。

■ $${\hat{R}}$$で収束確認
収束の確認をします。
指標$${\hat{R}}$$（あーるはっと）の値が$${1.1}$$以下のとき、収束したこととします。
次のコードでは$${\hat{R}>1.01}$$のパラメータの個数をカウントします。
個数が０ならば、$${\hat{R} \leq1.1}$$なので収束したとみなします。

### r_hat>1.1の確認
# 設定
idata_in = idata6        # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R}>1.01}$$のパラメータは０個でした。
$${\hat{R} \leq1.1}$$なので収束したとみなします。

■ $${\hat{R}}$$の値把握と事後統計量の表示

### 事後統計量の表示
pm.summary(idata6, hdi_prob=0.95)

【実行結果】

■ トレースプロットで収束確認
トレースプロットを描画します。
こちらの図でも収束の確認を行えます。

### トレースプロットの描画
pm.plot_trace(idata6, compact=True)
plt.tight_layout();

【実行結果】
左プロットの線の重なり具合、右プロットの偏りのない乱雑さより、収束している感じがします。

4. 分析

個体数の期待値$${\lambda}$$の事後分布を描画します。
テキストの図8に相当します。

### 観測値と期待値λを描画 ※図8に相当

## 描画用データの作成
# λの取り出し shape=(50, 4000)
lam_samples = idata6.posterior.lam.stack(sample=('chain','draw')).data
# λの事後平均の算出
lam_means = lam_samples.mean(axis=1)
# λの95%HDIの算出
lam_95hdi = az.hdi(lam_samples.T).T

## 描画
# 描画領域の指定
plt.figure(figsize=(6, 4))
ax = plt.subplot()
# 観測値の散布図の描画
ax.scatter(data2.X, data2.Y, s=15, color='blue', label='観測値')
# λの事後平均の折れ線グラフの描画
ax.plot(data2.X, lam_means, color='red', label=r'$\lambda$の事後平均')
# λの95%HDIの描画
ax.fill_between(data2.X, lam_95hdi[0], lam_95hdi[1], color='tomato', alpha=0.2,
                label='95%HDI')
# 修飾
ax.set(ylim=(-1, 26), xlabel='位置', ylabel='個体数',
        title='個体数の期待値の予測\nIntrinsic CARモデル')
ax.legend()
ax.grid(lw=0.5)
plt.show()

【実行結果】
赤い線が$${\lambda}$$の事後分布の平均値、ピンクの面が$${\lambda}$$の95%HDI区間です。
青点の観測値は期待値$${\lambda}$$の95%HDIにだいたい収まっているようです。

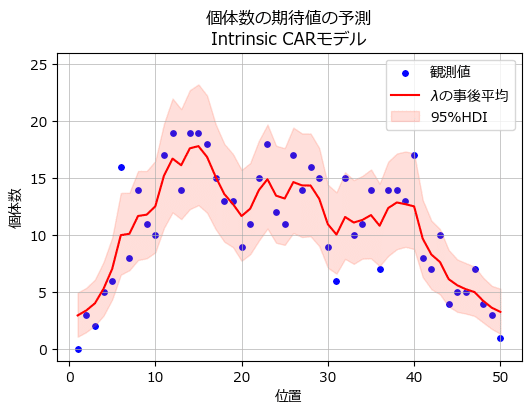
一般化線形混合モデルの予測値グラフと比べてみましょう。
ICARモデルの事後平均の赤い線は一般化線形混合モデルよりも滑らかになっています。
テキストによると「Intrinsic CARモデルでは、隣の調査地との空間構造をモデルに取り入れているため」とあります。

5. 推論データの保存

pickle で MCMCサンプリングデータ idata6 を保存できます。

### 推論データの保存
file = r'idata6_ch3.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata6, f)

次のコードで保存したファイルを読み込みできます。

### 推論データの読み込み
file = r'idata6_ch3.pkl'
with open(file, 'rb') as f:
    idata6_ch3_load = pickle.load(f)

ベイズモデル～ローカルレベルモデル

1. 状態空間モデルとCARモデル

テキストによると、1次元1階差分のIntrinsic CAR モデルはローカルレベルモデルと同じ中身を別の形式で表現したものとのことです。
早速ローカルレベルモデルを試してみましょう！

2. モデルの定義

テキストのローカルレベルモデルの実装を真似ています。
システムモデルに pm.GaussianRandomWalk() を利用します。

### モデルの定義
with pm.Model() as model7:

    ### データ関連定義
    # coordの定義
    model7.add_coord('data', values=data2.index, mutable=True)
    # dataの定義
    y = pm.ConstantData('y', value=data2.Y.values, dims='data')

    ### 事前分布
    # ランダムウォークの標準偏差
    sigma = pm.Uniform('sigma', lower=0, upper=100)
    
    ### システムモデル：ランダムウォーク
    init_dist = pm.Uniform.dist(lower=0, upper=10)
    alpha = pm.GaussianRandomWalk('alpha', mu=0, sigma=sigma,
                                  init_dist=init_dist, dims='data')

    ### 尤度　観測モデル：ポアソン分布
    lam = pm.Deterministic('lam', pt.exp(alpha), dims='data')
    Y = pm.Poisson('Y', mu=lam, observed=y, dims='data')

モデルの内容を表示・可視化してみましょう。

### モデルの表示
model7

【実行結果】

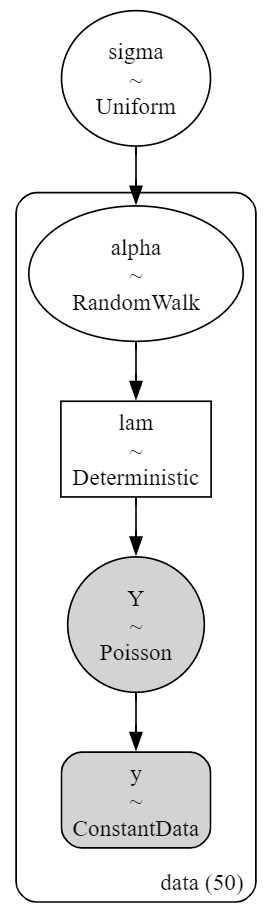
続いてモデルを可視化します。

### モデルの可視化
pm.model_to_graphviz(model7)

【実行結果】
ローカルレベルモデルのほうが少ないパラメータで表現できるのでシンプルです。

3. MCMCの実行と収束の確認

### 事後分布からのサンプリング 10秒
# NUTSの初期値を設定しなくても収束した
with model7:
    idata7 = pm.sample(draws=1000, tune=1000, chains=4, random_seed=123,
                       target_accept=0.99, nuts_sampler='numpyro')

【実行結果】
処理時間は10秒です。

### r_hat>1.1の確認
# 設定
idata_in = idata7        # idata名
threshold = 1.01         # しきい値

# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())

【実行結果】
$${\hat{R}>1.01}$$のパラメータは０個でした。
$${\hat{R} \leq1.1}$$なので収束したとみなします。

■ $${\hat{R}}$$の値把握と事後統計量の表示

### 事後統計量の表示
pm.summary(idata7, hdi_prob=0.95)

【実行結果】

■ トレースプロットで収束確認
トレースプロットを描画します。
こちらの図でも収束の確認を行えます。

### トレースプロットの描画
pm.plot_trace(idata7, compact=True)
plt.tight_layout();

【実行結果】
左プロットの線の重なり具合、右プロットの偏りのない乱雑さより、収束している感じがします。

と言いたいところですが、グラフ下部に黒いバーコード線が多数付いています。
MCMCサンプリングデータに発散しているデータが含まれています。
あまりいい状況ではなさそうです・・・
ICARモデルは発散データが無かったです。不思議です・・・

4. 分析

個体数の期待値$${\lambda}$$の事後分布を描画します。
テキストの図9に相当します。

### 観測値と期待値λを描画 ※図9に相当

## 描画用データの作成
# λの取り出し shape=(50, 4000)
lam_samples = idata7.posterior.lam.stack(sample=('chain','draw')).data
# λの事後平均の算出
lam_means = lam_samples.mean(axis=1)
# λの95%HDIの算出
lam_95hdi = az.hdi(lam_samples.T).T

## 描画
# 描画領域の指定
plt.figure(figsize=(6, 4))
ax = plt.subplot()
# 観測値の散布図の描画
ax.scatter(data2.X, data2.Y, s=15, color='blue', label='観測値')
# λの事後平均の折れ線グラフの描画
ax.plot(data2.X, lam_means, color='red', label=r'$\lambda$の事後平均')
# λの95%HDIの描画
ax.fill_between(data2.X, lam_95hdi[0], lam_95hdi[1], color='tomato', alpha=0.2,
                label='95%HDI')
# 修飾
ax.set(ylim=(-1, 26), xlabel='位置', ylabel='個体数',
        title='個体数の期待値の予測\nローカルレベルモデル')
ax.legend()
ax.grid(lw=0.5)
plt.show()

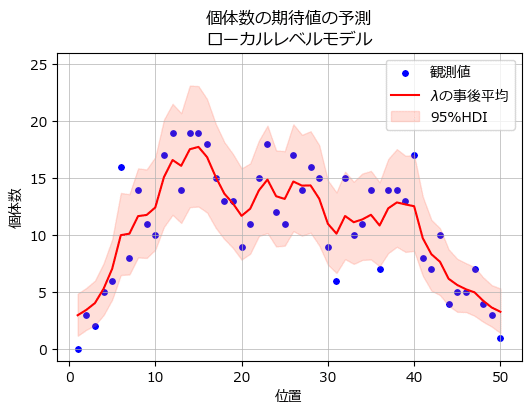
ICARモデルの事後分布とほぼ同じですね（違いもあるようです）。

5. 推論データの保存

pickle で MCMCサンプリングデータ idata7 を保存できます。

### 推論データの保存
file = r'idata7_ch3.pkl'
with open(file, 'wb') as f:
    pickle.dump(idata7, f)

次のコードで保存したファイルを読み込みできます。

### 推論データの読み込み
file = r'idata7_ch3.pkl'
with open(file, 'rb') as f:
    idata7_ch3_load = pickle.load(f)

ベイズ記事は以上です。

次回予告

「時系列・空間データのモデリング」章
　空間自己回帰モデル「2次元の株数カウントデータ」

結び

この記事では多くの未知コードに遭遇しました。
中でも一番難儀したのが一般化線形混合モデル。
Pythonで動く複雑な統計モデリングツールを探すのは大変です。
一方でベイズのICARモデルはPyMCで難儀すること無く利用できました。
ベイズモデルの基礎には一般化線形混合モデル等の統計モデルが位置づけられるような気がしています。
Pythonに統計モデルツールが充実するように、と短冊に書こうかしら？

おわり

シリーズの記事

次の記事

前の記事

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルはＲ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。

いいなと思ったら応援しよう！

この記事が参加している募集

#新生活をたのしく

46,893件

実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で⑨空間自己回帰モデル：1次元の個体数カウントデータ

「時系列・空間データのモデリング」章

はじめに

岩波データサイエンスVol.1の紹介

引用表記

PyMC環境の準備

イントロ

1. モデルのイメージ

2. インポート

3. データの読み込み

4. データの外観の確認

5. 一般化線形混合モデル

ベイズモデル ～ ICARモデル

1. モデル数式

2. モデルの定義

3. MCMCの実行と収束の確認

4. 分析

5. 推論データの保存

ベイズモデル ～ ローカルレベルモデル

1. 状態空間モデルとCARモデル

2. モデルの定義

3. MCMCの実行と収束の確認

4. 分析

5. 推論データの保存

次回予告

結び

シリーズの記事

ブログの紹介

いいなと思ったら応援しよう！

この記事が参加している募集

ベイズモデル～ ICARモデル

ベイズモデル～ローカルレベルモデル