
「Pythonによる異常検知」を寄り道写経 ~ 第2章2.2節「正規分布に基づく異常検知」
第2章「非時系列データにおける異常検知」
書籍の著者 曽我部東馬 先生、監修 曽我部完 先生
この記事は、テキスト「Pythonによる異常検知」第2章「非時系列データにおける異常検知」2.2節「正規分布に基づく異常検知」の通称「寄り道写経」を取り扱います。
今回から異常検知がはじまります!
データが正規分布に従うと仮定できる場合の異常検知を寄り道写経します!ではテキストを開いて異常検知の旅に出発です🚀

はじめに
テキスト「Pythonによる異常検知」のご紹介
このシリーズは書籍「Pythonによる異常検知」(オーム社、「テキスト」と呼びます)の寄り道写経です。
テキストは、2021年2月に発売され、機械学習等の誤差関数から異常検知を解明して、異常検知に関する実践的なPythonコードを提供する素晴らしい書籍です。
とにかく「誤差関数」と「異常度」の強い結びつきを堪能できる1冊です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonによる異常検知」第1版第6刷、著者 曽我部東馬、監修者 曽我部完、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
2.2 正規分布に基づく異常検知
主に Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
今回の寄り道ポイントです。
すべて学習データのみ使用する異常検知となります。
データが1次元正規分布に従う場合の異常検知
異常度の閾値に分位点法を用いる
異常度の閾値にホテリングの$${T^2}$$法を用いる
データが2次元正規分布に従う場合の異常検知
異常度の閾値にホテリングの$${T^2}$$法を用いる

この記事で用いるライブラリをインポートします。
### インポート
# 数値計算、確率計算
import numpy as np
import pandas as pd
import scipy.stats as stats
# 距離計算
from scipy.spatial import distance
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
2.2.1 1次元正規分布に基づく異常検知
1.異常度の定義
テキストの数式をお借りして、正規分布データにおける異常度を定義します。
【正規分布データにおける異常度$${\alpha}$$の定義】
$$
\alpha = \cfrac{(\boldsymbol{x} - \mu)^2}{\sigma^2}
$$
$${\mu}$$はデータの平均、$${\sigma^2}$$はデータの分散です。
2.正規分布と異常度の関係図
テキストの図2.3をお借りして、正規分布の確率密度関数と異常度を可視化します。
### 図2.3 平均値との距離の図、分散と異常度の関係図
# 正規分布のパラメータ設定
mu = 3
sigmas = [1, 1.3, 0.18]
# 描画用の設定
ylims = [(0, 1), (0, 2), (0, 5)]
titles = ['', '$\sigma^2$ が大きい', '$\sigma^2$ が小さい']
# x軸の値の設定
xval = np.linspace(1, 5, 1001)
## 描画処理
# 描画領域の設定
fig, ax = plt.subplots(1, 3, figsize=(10, 4))
# 3つのグラフ描画を繰り返し処理
for i in range(3):
# 正規分布の確率密度関数の算出
prob_dens = stats.norm.pdf(xval, loc=mu, scale=sigmas[i])
# 異常度αの算出
alpha_vals = (xval - mu)**2 / sigmas[i]**2
# 正規分布の確率密度関数の描画
ax[i].plot(xval, prob_dens, color='tab:blue')
# 異常度αの描画
ax[i].plot(xval, alpha_vals, color='tab:red', ls='--')
# μの垂直線の描画
ax[i].axvline(mu, color='black', ls=':', lw=0.5)
# axes単位の修飾1
ax[i].set(ylim=ylims[i], yticks=[], title=titles[i])
# axes単位の修飾2
ax[0].text(x=2.94, y=-0.2, s='$\mu$')
ax[1].text(x=2.93, y=-0.4, s='$\mu$')
ax[2].text(x=2.93, y=-1.0, s='$\mu$')
# 凡例
plt.plot([], [], color='tab:blue', label='1次元正規分布')
plt.plot([], [], color='tab:red', ls='--', label=r'異常度$\alpha$')
fig.legend(bbox_to_anchor=(0.01, 0.85), ncols=2, loc='lower left')
# 全体修飾
fig.suptitle(r'正規分布と異常度 $\alpha$')
plt.tight_layout();【実行結果】
正規分布の確率密度関数と異常度は凸の向きが逆になっています。
赤い点線の異常度は正規分布の平均(峰)が最小値になります。

分散$${\sigma^2}$$が大きい場合に異常度の放物線は緩やかになり、分散が小さい場合に異常度の放物線は鋭くなります。
データの平均値からの距離が同一の場合、分散が大きい方が異常度の値が小さく、分散が小さい方が異常度の値が大きくなります。

3.データの読み込み
テキストで用いる「Davisデータセット」を読み込みます。
Davisデータセットは R の carData パッケージに含まれており、次のWebサイトから取得できます。
No.211 のデータセットです。

Webサイトから直接読み込みましょう。
### データの読み込み
# URLより直接データを読み込み
URL = 'https://vincentarelbundock.github.io/Rdatasets/csv/carData/Davis.csv'
data = pd.read_csv(URL, usecols=[1, 2, 3, 4, 5])
# データの表示
print('data.shape', data.shape)
display(data.head())【実行結果】
200名の体重・身長データです。
この記事では、体重: weight(kg)と身長: height(cm)を利用します。

4.データの外観の確認
要約統計量を確認しましょう。
### データの要約統計量
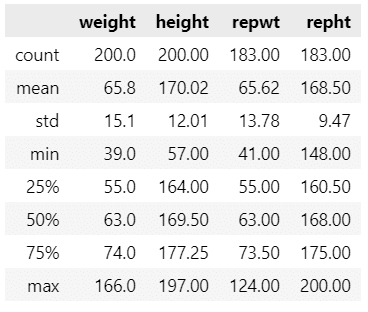
data.describe().round(2)【実行結果】
体重の最大値が突出している感じがします。
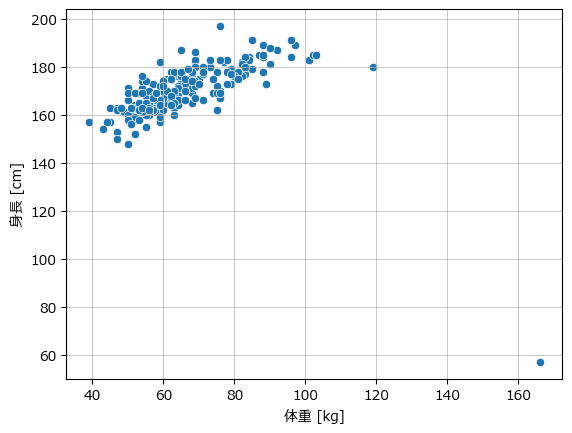
体重と身長の散布図を確認しましょう。
### データの可視化
sns.scatterplot(data=data, x='weight', y='height')
plt.xlabel('体重 [kg]')
plt.ylabel('身長 [cm]')
plt.grid(lw=0.5)【実行結果】
体重 160 kg あたりに外れ値的なデータ点があります。
おそらくこの点は異常値に判定されると思います(予告)。

1次元正規分布に従うデータを分位点法を用いて異常検知
体重データで異常検知に臨みます!
1.データセットの作成
### データセットの作成 1次元の変数x:体重データ
x = data['weight'].values
print('x.shape: ', x.shape)
print(x[:10], '...')【実行結果】

2.データが正規分布に従うことの確認
テキストにならって、ヒストグラム等の可視化により正規分布に近似しているかどうかを確認します。
テキストの図2.4に相当します。
データを正規分布にフィッティングさせて平均パラメータ・標準偏差パラメータを取得する練習をします。
scipy.stats を用います。
stats.norm.fit(x)【実行結果】
フィッティングの結果、平均 65.8、標準偏差 15.06 の正規分布パラメータを得ました。

実は テキストで用いる「distplot」は現在「非推奨」であり、seaborn が v.0.14.0 のときに削除されます。
そこで、distplot を使わない実装をしてみようと思います。
sns.lineplot() 内で用いている「*stats.norm.fit(x)」は、先程練習したデータを正規分布にフィッティングするコードです。
### 図2.4 変数xのヒストグラムと正規分布フィッティング
# ★テキストのdistplotは廃止された
# 描画領域の設定
fig, ax = plt.subplots(figsize=(7, 4))
# xのヒストグラムの描画
sns.histplot(x=x, bins=50, stat='density', ec='white', alpha=0.5,
label='ヒストグラム分布', ax=ax)
# xをフィットさせた正規分布の確率密度関数の描画
xval = np.linspace(x.min()-20, x.max(), 101)
sns.lineplot(x=xval, y=stats.norm.pdf(xval, *stats.norm.fit(x)),
color='tab:red', label='正規分布近似', ax=ax)
# rug(x軸線上のバーコード)の描画
sns.rugplot(x=x, height=0.05, color='royalblue', ax=ax)
# 修飾
ax.set(xlabel='体重 [kg]', ylabel='確率密度', title='$Davis$ データセット')
ax.grid(lw=0.5)
ax.legend();【実行結果】
テキストはヒストグラムの形状からデータが正規分布に近似していると判断しています。


3.異常度の算出
異常度の定義の数式にのっとって、異常度を算出します。
### 異常度の算出
# 異常度算出基礎の作成
x_mean = x.mean(axis=0) # 学習データの平均
x_var = x.var(ddof=0) # 学習データの分散(標本分散)
print('学習データの平均:', x_mean)
print('学習データの分散:', x_var)
# 異常度αの算出 α = (x - μ)² / σ²
alpha = (x - x_mean)**2 / x_var
print('\n異常度 alpha.shape: ', alpha.shape)
print(alpha[:10], '…')【実行結果】

前半は学習データの平均と分散です。
未知データの異常検知をする際に、この学習データの平均と分散を使いますので、必要に応じて保存しておきます。
後半は異常度です。
200サンプルのうち先頭10件を表示しています。
4.異常度の閾値の算出
分位点法で閾値を算出します。
ここでは 1% を分位点とします(テキストは 3%)。
200サンプルあるので、$${200 \times 0.01 = 2}$$。
異常度を大きい順に並べて2つ目のデータ点の異常値を閾値にします。
### 分位点法による異常度の閾値の算出
## 異常度の閾値・上側%の設定
q_point = 0.01
## 異常度の閾値の算出 分位点法
# 異常データ数の算出
n_err = int(len(x) * q_point)
print('\n異常データ数: ', n_err)
# 異常度の大きい順でn_err番目の値を取得
threshold = sorted(alpha)[::-1][n_err - 1]
print('異常度の閾値: ', threshold)【実行結果】
異常度の閾値はおよそ 12.48 です。

5.異常度のプロット
テキストの図2.5に相当する異常度の可視化を行ってみます。
1つ目は異常度のヒストグラムです。
### 図2.5左 異常度のヒストグラム
# 描画領域の設定
fig, ax = plt.subplots(figsize=(7, 4))
# 異常度のヒストグラム
sns.histplot(x=alpha, element='step', stat='probability', alpha=0.2, ax=ax)
# 異常度のrugプロット(足元のバーコード)の描画
sns.rugplot(x=alpha, height=0.05, color='royalblue', ax=ax)
# 閾値の垂直線の描画
ax.axvline(threshold, color='tab:red', ls='--', label='閾値')
# 修飾
ax.set(xlabel=r'異常度$\alpha$', ylabel='確率[%]',
title=f'異常度 $\\alpha$ のヒストグラム\n'
f'{q_point:.0%}分位点法による閾値 {threshold:.3f}')
ax.grid(lw=0.5)
ax.legend();【実行結果】
赤い垂直線の閾値から右側が異常値ゾーンです。
めっちゃ 0 付近に集中しています。
一方で 40 を超える異常度のデータ点も存在します。

2つ目は散布図です。
### 図2.5右 異常検知実行例
# 正常/異常のラベル設定 0:正常, 1:異常
error_labels = (alpha >= threshold) + 1
# 描画領域の設定
fig, ax = plt.subplots(figsize=(7, 5))
# 異常度の散布図の描画
sns.scatterplot(x=range(1, len(alpha)+1), y=alpha, alpha=0.6,
hue=error_labels, palette=['tab:blue', 'tab:red'],
size=error_labels, sizes=[30, 80], ax=ax)
# 閾値の水平線の描画
ax.axhline(threshold, color='tab:red', ls='--', label='閾値')
# 凡例
handles, _ = ax.get_legend_handles_labels()
ax.legend(title='凡例', handles=handles, labels=['正常', '異常', '閾値'])
# 修飾
ax.set(xlabel=r'データ番号', ylabel=r'異常度 $\alpha$',
title=f'異常度 $\\alpha$ の散布図\n'
f'{q_point:.0%}分位点法による閾値 {threshold:.3f}')
ax.grid(lw=0.5);【実行結果】
こちらの図の方が正常データと異常データの判別が分かりやすいかもです。
テキストの縦軸の異常度とスケールが違っていますが、理由は不明です。


1次元正規分布に従うデータをホテリングのT²法を用いて異常検知
引き続き体重データで異常検知に臨みます!
データセットを行列扱いすることに伴い、異常度の定義も行列計算に変形します。
$$
\alpha(\boldsymbol{x}) =(\boldsymbol{x}-\boldsymbol{\mu}) \boldsymbol{\Sigma}^{-1} (\boldsymbol{x}-\boldsymbol{\mu})
$$
$${\boldsymbol{\mu}}$$はデータの平均、$${\boldsymbol{\Sigma}^{-1}}$$はデータの分散共分散行列の逆行列です。

1.データセットの作成
2次元に編集します。
### データセットの作成 体重データをshape=(200, 1)の行列に変換
x_mtx = data['weight'].values.reshape(-1, 1)
print('x_mtx.shape:', x_mtx.shape)
print(x_mtx[:5], '…')【実行結果】

2.異常度の算出
異常度は2つの方法で計算します。
1つ目は異常度の定義の数式どおりに算出します。
2つ目は異常度の定義の数式を scipy のマハラノビス距離関数を用いて算出します。
### 異常度の算出
# 異常度算出基礎の作成(学習データの平均、分散共分散行列の逆行列)
x_mtx_mean = x_mtx.mean(axis=0) # 学習データの平均
x_mtx_cov = np.cov(x_mtx.T, ddof=0).reshape(-1, 1) # 学習データの分散共分散行列
x_mtx_cov_inv = np.linalg.inv(x_mtx_cov) # 学習データの分散共分散行列の逆行列
print('x_mtx_mean :', x_mtx_mean)
print('x_mtx_cov_inv:', x_mtx_cov_inv)
# 異常度αの算出 方法1:行列計算
x_mtx_centered = x_mtx - x_mtx_mean
alpha_hot1 = (x_mtx_centered @ x_mtx_cov_inv * x_mtx_centered).flatten()
print('\nanomaly1 : ', alpha_hot1[:5], '…')
# 異常度αの算出 方法2:マハラノビス距離の二乗
alpha_hot2 = np.array(
[distance.mahalanobis(u, x_mtx_mean, x_mtx_cov_inv)**2 for u in x_mtx])
print('anomaly2 : ', alpha_hot2[:5], '…')【実行結果】

前半は学習データの平均と分散共分散行列の逆行列です。
未知データの異常検知をする際に、この学習データの平均と分散共分散行列の逆行列を使いますので、必要に応じて保存しておきます。
後半は異常度です。
1つ目の行列計算の結果とマハラノビス距離の二乗の結果は一致しています。
3.異常度の閾値の算出
カイ二乗分布を用いて閾値を算出します。
ここでは 1% を分位点とします(テキストも 1%)。
またデータの次元数$${M=1}$$ですのでカイ二乗分布の自由度は1です。
閾値は自由度1のカイ二乗分布の上側1%点です。
### ホテリングのT²法による異常度の閾値の算出
# 異常度の閾値・上側%の設定
q_point = 0.01
# 異常度の閾値の算出:自由度1のカイ二乗分布の上側q_point%点
threshold = stats.chi2.isf(q=q_point, df=1)
print('\nthreshold : ', threshold)【実行結果】
異常度の閾値はおよそ 6.63 です。

4.異常度のプロット
テキストの図2.6に相当する異常度の可視化を行ってみます。
### 図2.6 ホテリング法による異常度閾値の設定
# 正常/異常ラベルの設定 0:正常, 1:異常
error_labels = (alpha_hot1 > threshold) + 0
# 描画領域の設定
fig, ax = plt.subplots(figsize=(7, 4))
# 異常度の散布図の描画
sns.scatterplot(x=range(len(x_mtx)), y=alpha_hot1, hue=error_labels,
palette=['tab:blue', 'tab:red'], alpha=0.6, ec='bisque',
size=error_labels, sizes=[40, 80], ax=ax)
# 閾値の水平線の描画
ax.axhline(threshold, color='tab:red', ls='--', label='xxxxx')
# 凡例
handles, _ = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=['正常', '異常', f'閾値'],
title='凡例')
# 修飾
ax.set(xlabel='データ番号', ylabel='異常度 $\\alpha$',
title='異常度 $\\alpha$ の散布図\n'
f'ホテリング法による閾値:{threshold:.3f}\n'
f'(自由度1のカイ二乗分布の上側{q_point:.0%}点)')
ax.grid(lw=0.5);【実行結果】
うまく異常データを識別できている感じがします。
テキストの縦軸の異常度とスケールが違っていますが、理由は不明です。


2.2.2 多次元正規分布に基づく異常検知
体重&身長の2次元データで異常検知に臨みます!
1.データセットの作成
体重と身長のデータセットを作成します。
### データの作成 体重と身長で2次元データを作成
data_mtx = data[['weight', 'height']].values
print('data_mtx.shape:', data_mtx.shape)
print(data_mtx[:5], '…')【実行結果】

2.異常度の算出
異常度は2つの方法で計算します。
1つ目は異常度の定義の数式どおりに算出します。
2つ目は異常度の定義の数式を scipy のマハラノビス距離関数を用いて算出します。
### 異常度の算出
# 異常度算出基礎の作成(学習データの平均、分散共分散行列の逆行列)
mean_mtx = data_mtx.mean(axis=0) # 学習データの平均
cov_mtx = np.cov(data_mtx.T, ddof=0) # 学習データの分散共分散行列
cov_inv_mtx = np.linalg.inv(cov_mtx) # 学習データの分散共分散行列の逆行列
print('mean_mtx:', mean_mtx)
print('cov_inv_mtx:')
print(cov_inv_mtx)
# 異常度αの算出 方法1 列ごとに異常度を計算して行ごとに合計をとる
data_mtx_c = data_mtx - mean_mtx # データの中心化
anomaly_score = (data_mtx_c @ cov_inv_mtx * data_mtx_c).sum(axis=1)
print('\nanomaly_score.shape:', anomaly_score.shape)
print(anomaly_score[:5], '…')
# 異常度αの算出 方法2 マハラノビス距離の二乗
anomaly_score2 = np.array(
[distance.mahalanobis(u, mean_mtx, cov_inv_mtx)**2 for u in data_mtx])
print('\nanomaly_score2.shape:', anomaly_score2.shape)
print(anomaly_score2[:5], '…')【実行結果】

前半は学習データの平均と分散共分散行列の逆行列です。
未知データの異常検知をする際に、この学習データの平均と分散共分散行列の逆行列を使いますので、必要に応じて保存しておきます。
後半は異常度です。
1つ目の行列計算の結果とマハラノビス距離の二乗の結果は一致しています。
3.異常度の閾値の算出
カイ二乗分布を用いて閾値を算出します。
ここでは 1% を分位点とします(テキストは 2%)。
またデータの次元数$${M=2}$$ですのでカイ二乗分布の自由度は2です。
閾値は自由度2のカイ二乗分布の上側1%点です(※)。
あわせて、正常・異常ラベルも作成します。
※テキストは自由度1を用いています。理由は不明です。
### ホテリングのT²法による異常度の閾値の算出
# 設定
gamma = 0.01 # 閾値に用いる分位点
nu = data_mtx.shape[1] # 閾値に用いるカイ二乗分布の自由度 変数の次元数(M=2)
# 異常度の閾値の算出 自由度2のカイ二乗分布の上側1%点
threshold = stats.chi2.isf(q=gamma, df=nu)
print('\nthreshold:', threshold)
# 正常/異常ラベルの算出 0:正常, 1:異常
anomaly_labels = (anomaly_score > threshold) + 0
print('\nanomaly_labels.shape:', anomaly_labels.shape)
print(anomaly_labels[:25], '…')【実行結果】
異常度の閾値はおよそ 9.21 です。
2つ目のデータは正常 0・異常 1 のラベルデータです。

4.異常度のプロット
テキストの図2.8に相当する異常度の可視化を行ってみます。
1つ目は体重・身長の散布図です。
### 図2.8 別バージョン:異常度の閾値を表現
## マハラノビス距離の算出
# scipy.distance利用 引数: (データ1, データ2), 平均, 分散共分散行列の逆数
pos_3d = np.array([[(i, j, distance.mahalanobis((i, j), mean_mtx, cov_inv_mtx))
for i in np.arange(20, 210)]
for j in np.arange(20, 210)])
## 描画処理
# 描画領域の設定
fig, ax = plt.subplots(figsize=(7, 5))
# 観測値の散布図の描画
sns.scatterplot(data=data, x='weight', y='height', ax=ax)
# 等高線図の描画
ax.contour(pos_3d.T[0], pos_3d.T[1], pos_3d.T[2], levels=20, cmap='Greens_r',
vmin=0, vmax=18, linewidths=0.5)
# 閾値の描画 自由度「1」のカイ二乗分布の上側2%点
ax.contour(pos_3d.T[0], pos_3d.T[1], pos_3d.T[2],
levels=[np.sqrt(stats.chi2.isf(q=gamma, df=1))],
colors=['tab:red'], linestyles=['--'])
# 凡例
ax.plot([], [], color='tab:red', ls='--', label='閾値')
ax.legend()
# 修飾
ax.set(xlabel='体重 [kg]', ylabel='身長 [cm]',
title='2変数の異常検知:観測値とマハラノビス距離の等高線')
plt.grid(lw=0.5);【実行結果】
等高線上は同じ異常度です。
赤い点線が異常度の閾値です。
右下の外れ値的なデータ点は中心点の等高線からかなり遠距離の等高線に位置しています。

2つ目は異常度の散布図です。
### 図2.8右 異常度の描画
# 描画領域の設定
fig, ax = plt.subplots()
sns.scatterplot(x=range(len(anomaly_score)), y=anomaly_score, hue=anomaly_labels,
palette=['tab:blue', 'tab:red'], alpha=0.6, ec='bisque',
size=anomaly_labels, sizes=[40, 80], ax=ax)
ax.axhline(threshold, color='tab:red', ls='--', label=f'閾値 {threshold:.3f}')
# 凡例
handles, _ = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=['正常', '異常', f'閾値'],
title='凡例')
# 修飾
ax.set(xlabel='データ番号', ylabel='異常度 $\\alpha$',
title='異常度 $\\alpha$ の散布図\n'
f'ホテリング法による閾値:{threshold:.3f}\n'
f'(自由度{nu}のカイ二乗分布の上側{gamma:.0%}点)')
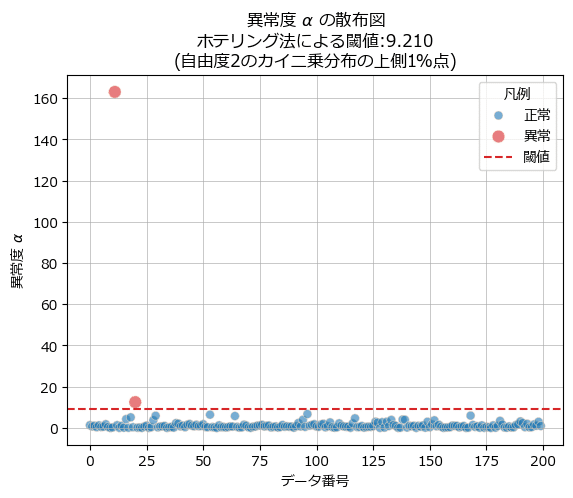
ax.grid(lw=0.5);【実行結果】
1次元のときよりも最大の異常度をもつデータ点が際立っている感じがします。
2番目に大きな異常度のデータ点を異常扱いしていいのか悩むますね。

2.2.3 多変数マハラノビス=タグチ法に基づく異常検知
マハラノビス=タグチ法を用いることで、異常度に関するデータの各変数の寄与がわかるそうです。
テキストオリジナルコードをお借りして、テキスト図2.9に相当する計算・描画をしてみます。
体重&身長の2次元データの使用を継続します。
### タグチ指標の計算(計算済みの中心化されたデータを利用)
# 異常データの番号の設定
number_data = 20
print('データ番号:', number_data)
# xとx-uの表示
print(f'x[{number_data}] :', data_mtx[number_data])
print(f'x[{number_data}]-μ:', data_mtx_c[number_data])
# σ²の表示
print('σ² :', np.diag(cov_mtx))
# タグチ指標SNの算出
SN = 10 * np.log10((data_mtx_c[number_data]**2 ) / np.diag(cov_mtx))
print ('\nTaguchi score is:')
print (SN)
# タグチ指標の描画 テキスト図2.9
fig, ax = plt.subplots(figsize=(5, 4))
sns.barplot(SN, width=0.4, color='tab:blue', alpha=0.8, ax=ax)
ax.axhline(0, color='black', lw=0.7, ls='--')
ax.set(xticks=[0, 1], xticklabels=['体重', '身長'], ylabel='タグチ指標 $SN$',
title='多変数マハラノビス=タグチ法に基づく異常検知\n'
f'$N^{{\prime}}=1,\ M_q=1$, データ点No.{number_data}');【実行結果】
データ点20は異常と判別されましたが、異常度算出の際、体重の寄与が大きいことが分かりました。


今回の寄り道写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
