
実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で⑦状態空間モデル:スギの年輪幅データ
「時系列・空間データのモデリング」章
テキスト「時系列・空間データのモデリング」の執筆者
伊東宏樹 先生
この記事は、テキストの「時系列・空間データのモデリング」章の「スギの年輪幅データを用いた状態空間モデル」の実践を取り扱います。
具体的には、テキストのスギ年輪幅データの時系列分析に用いる3つの状態空間モデル「ローカルレベルモデル」「トレンドモデル」「対数正規分布モデル」をPyMC化します。
この章を執筆された伊東先生は「たのしいベイズモデリング2」第5章を執筆されています。
樹木の直径と高さの数理モデルをベイズに取り込んでいます!
こちらもお楽しみくださいませ。
(ご参考)書籍「たのしいベイズモデリング2」
(ご参考)たのしいベイズモデリング2のPyMC化ブログ
はじめに
岩波データサイエンスVol.1の紹介
この記事は書籍「岩波データサイエンス vol.1」(岩波書店、以下「テキスト」と呼びます)の特集記事「ベイズ推論とMCMCのフリーソフト」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
テキストは、2015年10月に発売され、ベイズモデリングの様々なソフトウェアを用いたモデリング事例を多数掲載し、ベイズモデリングの楽しさを紹介する素晴らしい書籍です。
入門的なモデルから2次階差を取り扱う空間モデルまで、幅広い難易度のモデルを満喫できます!
このシリーズは、テキストのベイズモデルをPyMC Ver.5に書き換えて実践します。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「岩波データサイエンス vol.1」
第9刷、編者 岩波データサイエンス刊行委員会 岩波書店
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
PyMC環境の準備
Anacondaを用いる環境構築とGoogle ColaboratoryでPyMCを動かす方法について、次の記事にまとめています。
「PyMCを動かすまでの準備」章をご覧ください。
PythonとPyMC
テキストで利用するツールは、R、BUGS、JAGS です。
この記事では、PythonとPyMCを用いたコードに変換してベイズモデリングを実践いたします。
イントロ
1. 状態空間モデル
テキストの文章をお借りします。
状態空間モデルの特徴は、時系列に沿って変化する「状態」から「観測値」が得られると考えるところです。
「状態」は実際には観測されません。観測されるのは「観測値」のみです。
状態の変化を説明するモデルをシステムモデル(またはプロセスモデル)、状態から観測値が得られる過程を説明するモデルを観測モデル(またはデータモデル)と呼びます。
システムモデルを式で表現したものは状態方程式、観測モデルを指揮にしたものは測定方程式と呼ばれます。
ローカルレベルの例を図にしました。

青色が観測されない「状態」、赤色が観測される「観測値」です。
状態は時間の連鎖です。時間の流れ$${1, 2, \cdots, t-1, t}$$に乗って1つ前の時間の状態から次の時間の状態が生成されます。
観測値は時間的に同じタイミングの状態から生成されます。
2. インポート
「時系列・空間データのモデリング」章で利用するパッケージをインポートします。
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# WEBアクセス
import requests
# Rdata読み込み
import pyreadr
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')3. データの登録
Rコードに記載されているスギの年輪幅データを登録して、pandasのデータフレームを作成します。
### データの登録 example_code.Rより引用
width = (4.71, 7.70, 7.97, 8.35, 5.70, 7.33, 3.10, 4.98, 3.75, 3.35, 1.84,
3.28, 2.77, 2.72, 2.54, 3.23, 2.45, 1.90, 2.56, 2.12, 1.78, 3.18,
2.64, 1.86, 1.69, 0.81, 1.02, 1.40, 1.31, 1.57)
data1 = pd.DataFrame({'年輪幅': width}, index=range(1961, 1991))
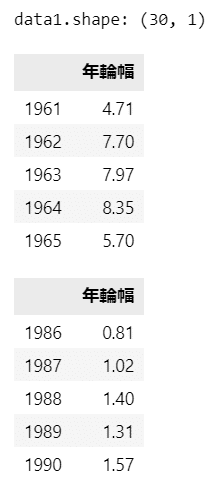
print('data1.shape:', data1.shape)
display(data1.head())
display(data1.tail())【実行結果】
京都市のある1本のスギの年輪幅30年間の観測データです。
4. データの外観の確認
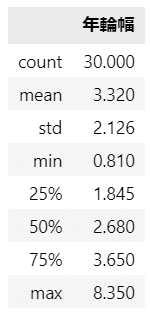
要約統計量を表示します。
### 要約統計量の表示
data1.describe().round(3)【実行結果】
樹の成長に伴い年輪幅は狭くなるので、最大値(max)は過去、最小値(min)は直前の時間軸かもしれません。
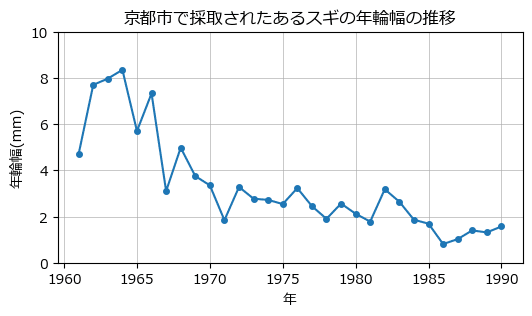
時系列の折れ線グラフを描画します。
テキストの図2に相当します。
### 時系列プロットの描画 ※図2に相当
fig, ax = plt.subplots(figsize=(6, 3))
ax.plot(data1, '-o', markersize=4)
ax.set(xlabel='年', ylabel='年輪幅(mm)', ylim=(0, 10),
title='京都市で採取されたあるスギの年輪幅の推移')
ax.grid(lw=0.5);【実行結果】
予測は見事に外れました。
最初の数年は年輪幅が広くなり、後半は 2mm 前後を行ったり来たりしています。
では、PyMCモデリングに進みます。
モデル1:ローカルレベルモデル
1. モデル数式
観測データから「状態」を推定します。
ローカルレベルモデルは次の式で表されます。
$$
\begin{align*}
y_t &= \alpha_t + \epsilon_t, \quad \epsilon_t \sim \text{Normal}\ (0,\ \sigma^2_{\epsilon}) \\
\alpha_t &= \alpha_{t-1} + \eta_{t}, \quad \eta_t \sim \text{Normal}\ (0,\ \sigma^2_{\eta}) \\
\end{align*}
$$
1行目は観測モデル(測定方程式)、2行目はシステムモデル(状態方程式)です。
システムモデルは時間に対して状態の値が少しずつ変化する(ランダムウォークする)と仮定されます。
2. モデルの定義
数式モデルに準拠してPyMCのモデルを定義しましょう。
システムモデルにはランダムウォーク「pm.GaussianRandomWalk()」を利用します。
### モデルの定義
with pm.Model() as model1:
### データ関連定義
# coordの定義
model1.add_coord('data', values=data1.index, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data1['年輪幅'].values, dims='data')
### 事前分布
sigmaEta = pm.Uniform('sigmaEta', lower=0, upper=100)
sigmaEpsilon = pm.Uniform('sigmaEpsilon', lower=0, upper=100)
### システムモデル
init_dist = pm.Uniform.dist(lower=0, upper=10)
alpha = pm.GaussianRandomWalk('alpha',sigma=sigmaEta, init_dist=init_dist,
dims='data')
### 尤度:観測モデル
Y = pm.Normal('Y', mu=alpha, sigma=sigmaEpsilon, observed=y, dims='data')2つの標準偏差の事前分布にはテキストどおり、0から100の区間の一様分布を仮定しました。
モデルの内容を表示・可視化してみましょう。
### モデルの表示
model1【実行結果】

続いてモデルを可視化します。
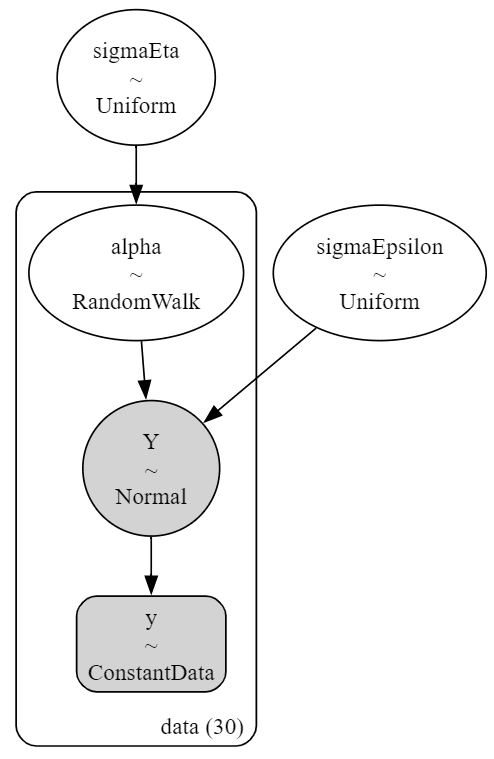
### モデルの可視化
pm.model_to_graphviz(model1)【実行結果】
シンプルなモデルですね!
alpha の RadomWalk は1期間前の alpha と自己相関する分布です。
3. MCMCの実行と収束の確認
■ MCMC
マルコフ連鎖=chainsを4本、バーンイン期間=tuneを1000、利用するサンプル=drawを1chainあたり1000に設定して、合計4000個の事後分布からのサンプリングデータを生成します。テキストの指定数とは異なっています。
サンプル方法に numpyro を指定しています。処理速度が早くなります。
numpyro を使わない場合は「nuts_sampler='numpyro',」を削除します。
### 事後分布からのサンプリング 10秒
with model1:
idata1 = pm.sample(draws=1000, tune=1000, chains=4, random_seed=123,
nuts_sampler='numpyro', target_accept=0.8)【実行結果】
処理時間は10秒です。
■ $${\hat{R}}$$で収束確認
収束の確認をします。
指標$${\hat{R}}$$(あーるはっと)の値が$${1.1}$$以下のとき、収束したこととします。
次のコードでは$${\hat{R}>1.01}$$のパラメータの個数をカウントします。
個数が0ならば、$${\hat{R} \leq1.1}$$なので収束したとみなします。
### r_hat>1.1の確認
# 設定
idata_in = idata1 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R}>1.01}$$のパラメータは0個でした。
$${\hat{R} \leq1.1}$$なので収束したとみなします。

■ $${\hat{R}}$$の値把握と事後統計量の表示
### 事後統計量の表示
var_names = ['sigmaEpsilon', 'sigmaEta', 'alpha']
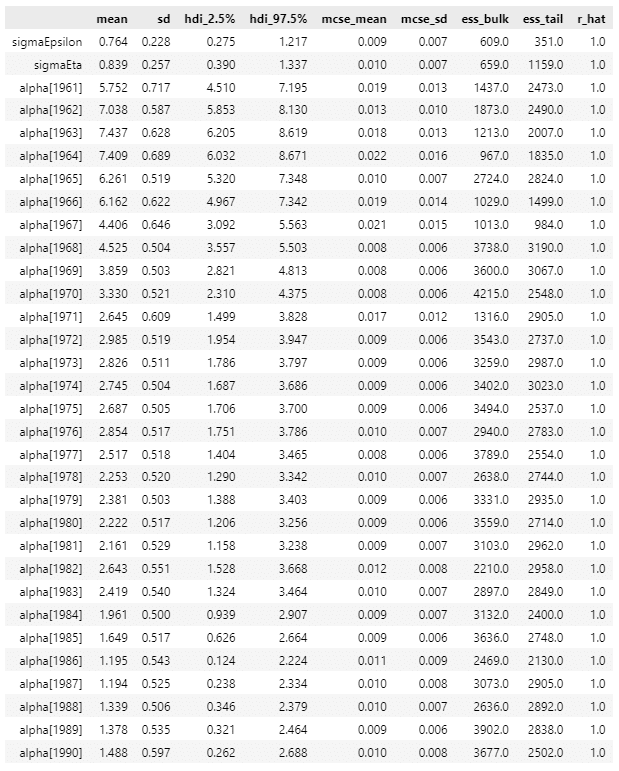
pm.summary(idata1, hdi_prob=0.95, var_names=var_names)【実行結果】
標準偏差パラメータ$${\sigma_{\epsilon},\ \sigma_{\eta}}$$はテキスト42ページと近い値になっています。
また状態 alpha には1961~1990年の推論値が表示されています。
■ トレースプロットで収束確認
トレースプロットを描画します。
こちらの図でも収束の確認を行えます。
### トレースプロットの描画
pm.plot_trace(idata1, compact=True, var_names=var_names)
plt.tight_layout();【実行結果】
左プロットの線の重なり具合、右プロットの偏りのない乱雑さより、収束している感じがします。

4. 分析
状態$${\alpha}$$の事後分布を描画しましょう。
テキストの図3に相当します。
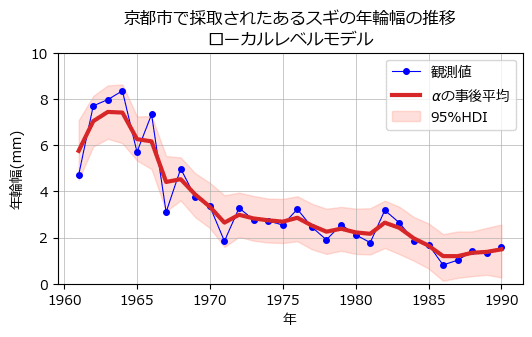
### 年輪幅の状態をローカルモデルで推定した例 ※図3に相当
## 描画用データの作成
# 事後分布サンプリングデータからαを取り出し
alpha_samples = idata1.posterior.alpha.stack(sample=('chain', 'draw')).data
# 年輪幅の期待値αの事後平均を算出
alpha_means = alpha_samples.mean(axis=1)
# 年輪幅の期待値αの95%HDIを算出
alpha_95hdi = az.hdi(alpha_samples.T).T
## 描画
fig, ax = plt.subplots(figsize=(6, 3))
# 観測値の折れ線グラフ
ax.plot(data1, '-o', markersize=4, color='blue', lw=0.8, label='観測値')
# αの事後平均の折れ線グラフ
ax.plot(data1.index, alpha_means, color='tab:red', lw=3,
label=r'$\alpha$の事後平均')
# αの95%HDIを塗りつぶし
ax.fill_between(data1.index, alpha_95hdi[0], alpha_95hdi[1], color='tomato',
alpha=0.2, label='95%HDI')
# 修飾
ax.set(xlabel='年', ylabel='年輪幅(mm)', ylim=(0, 10),
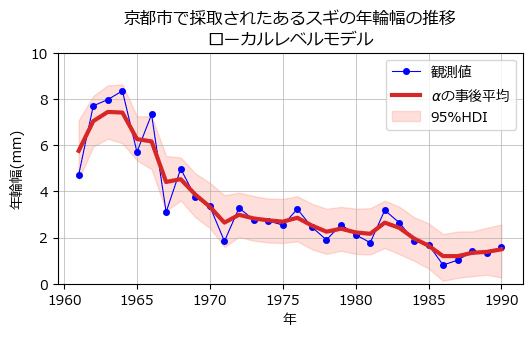
title='京都市で採取されたあるスギの年輪幅の推移\nローカルレベルモデル')
ax.grid(lw=0.5)
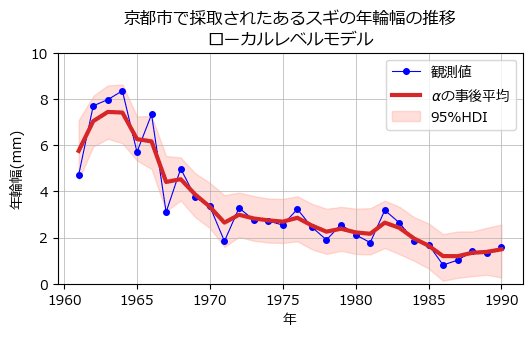
ax.legend();【実行結果】
赤い線が$${\alpha}$$の事後分布の平均値、ピンクの面が$${\alpha}$$の95%HDI区間です。
観測値の青点は95%HDIに収まっているようですので、ベイズ推論はうまくいっている感じがします。
5. 推論データの保存
pickle で MCMCサンプリングデータ idata1 を保存できます。
### 推論データの保存
file = r'idata1_ch3.pkl'
with open(file, 'wb') as f:
pickle.dump(idata1, f)次のコードで保存したファイルを読み込みできます。
### 推論データの読み込み
file = r'idata1_ch3.pkl'
with open(file, 'rb') as f:
idata1_ch3_load = pickle.load(f)モデル2:トレンドモデル
1. モデル数式
「状態」の変化量(傾き、トレンド)が少しずつを変化すると仮定するモデルです。
テキストは2次(2階)のトレンドモデルを扱っています。
次の式で表されます。
$$
\begin{align*}
\alpha_t - \alpha_{t-1} &= \alpha_{t-1} - \alpha_{t-2} + \eta_{t} \\
\Leftrightarrow \alpha_t &= 2\alpha_{t-1} - \alpha_{t-2} + \eta_{t} , \quad \epsilon_t \sim \text{Normal}\ (0,\ \sigma^2_{\epsilon}) \\
y_t &= \alpha_t + \epsilon_t, \quad \epsilon_t \sim \text{Normal}\ (0,\ \sigma^2_{\epsilon}) \\
\end{align*}
$$
2行目は観測モデル(測定方程式)、3行目はシステムモデル(状態方程式)です。
2. モデルの定義
数式モデルに準拠してPyMCのモデルを定義しましょう。
システムモデルには「pm.AR()」で2次の自己相関過程(自己相関係数$$\rho=[2,\ -1]$$)を構築します。
### モデルの定義
with pm.Model() as model2:
### データ関連定義
# coordの定義
model2.add_coord('data', values=data1.index, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data1['年輪幅'].values, dims='data')
### 事前分布
sigmaEta = pm.Uniform('sigmaEta', lower=0, upper=100)
sigmaEpsilon = pm.Uniform('sigmaEpsilon', lower=0, upper=100)
### システムモデル:AR(2)モデル
init_dist = pm.Uniform.dist(lower=0, upper=10)
alpha = pm.AR('alpha', rho=[2, -1], sigma=sigmaEta, constant=False,
init_dist=init_dist, ar_order=2, dims='data')
### 尤度:観測モデル
Y = pm.Normal('Y', mu=alpha, sigma=sigmaEpsilon, observed=y, dims='data')モデルの内容を表示・可視化してみましょう。
### モデルの表示
model2【実行結果】

続いてモデルを可視化します。
### モデルの可視化
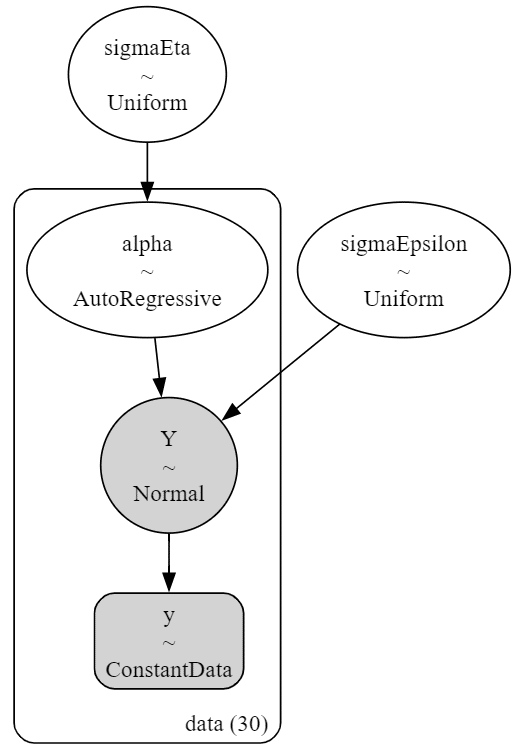
pm.model_to_graphviz(model2)【実行結果】
ローカルレベルモデルとよく似ています。
alpha の AuroRegressive(2次)は1期間前・2期間前の alpha と自己相関する分布です。
3. MCMCの実行と収束の確認
■ MCMC
マルコフ連鎖=chainsを4本、バーンイン期間=tuneを1000、利用するサンプル=drawを1chainあたり1000に設定して、合計4000個の事後分布からのサンプリングデータを生成します。テキストの指定数とは異なっています。
サンプル方法に numpyro を指定しています。処理速度が早くなります。
numpyro を使わない場合は「nuts_sampler='numpyro',」を削除します。
### 事後分布からのサンプリング 20秒
with model2:
idata2 = pm.sample(draws=1000, tune=1000, chains=4, random_seed=123,
nuts_sampler='numpyro', target_accept=0.992)【実行結果】
処理時間は20秒です。

■ $${\hat{R}}$$で収束確認
収束の確認をします。
指標$${\hat{R}}$$(あーるはっと)の値が$${1.1}$$以下のとき、収束したこととします。
上記基準を超える個数が0ならば、$${\hat{R} \leq1.1}$$なので収束したとみなします。
### r_hat>1.1の確認
# 設定
idata_in = idata2 # idata名
threshold = 1.02 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R}>1.1}$$のパラメータは0個でした。
$${\hat{R} \leq1.1}$$なので収束したとみなします。

■ $${\hat{R}}$$の値把握と事後統計量の表示
### 事後統計量の表示
var_names = ['sigmaEpsilon', 'sigmaEta', 'alpha']
pm.summary(idata2, hdi_prob=0.95, var_names=var_names)【実行結果】
ローカルレベルモデルのパラメータの事後分布とは少し異なる値になりました。

■ トレースプロットで収束確認
トレースプロットを描画します。
こちらの図でも収束の確認を行えます。
### トレースプロットの描画
pm.plot_trace(idata2, compact=True, var_names=var_names)
plt.tight_layout();【実行結果】
左プロットの線の重なり具合、右プロットの偏りのない乱雑さより、収束している感じがします。
ただ、グラフの下に見えるバーコードのような線で「発散」しているデータがあることが示されています。
発散はいい状態では無いことを意味します。

4. 分析
状態$${\alpha}$$の事後分布を描画しましょう。
テキストの図4に相当します。
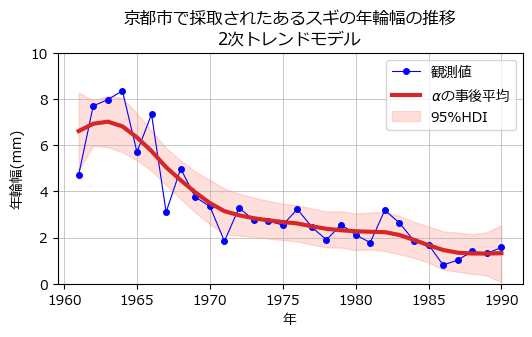
### 年輪幅の状態をトレンドモデルで推定した例 ※図4に相当
## 描画用データの作成
# 事後分布サンプリングデータからαを取り出し
alpha_samples = idata2.posterior.alpha.stack(sample=('chain', 'draw')).data
# 年輪幅の期待値αの事後平均を算出
alpha_means = alpha_samples.mean(axis=1)
# 年輪幅の期待値αの95%HDIを算出
alpha_95hdi = az.hdi(alpha_samples.T).T
## 描画
fig, ax = plt.subplots(figsize=(6, 3))
# 観測値の折れ線グラフ
ax.plot(data1, '-o', markersize=4, color='blue', lw=0.8, label='観測値')
# αの事後平均の折れ線グラフ
ax.plot(data1.index, alpha_means, color='tab:red', lw=3,
label=r'$\alpha$の事後平均')
# αの95%HDIを塗りつぶし
ax.fill_between(data1.index, alpha_95hdi[0], alpha_95hdi[1], color='tomato',
alpha=0.2, label='95%HDI')
# 修飾
ax.set(xlabel='年', ylabel='年輪幅(mm)', ylim=(0, 10),
title='京都市で採取されたあるスギの年輪幅の推移\n2次トレンドモデル')
ax.grid(lw=0.5)
ax.legend();【実行結果】
赤い線が$${\alpha}$$の事後分布の平均値、ピンクの面が$${\alpha}$$の95%HDI区間です。
ローカルレベルモデルよりも事後平均の線が滑らかになり、やや95%HDIの幅が狭くなっている感じがします。
観測値の青点は若干95%HDIから漏れているものがありますが、全体的にはいい感じに当てはまっていると思います!
(参考:ローカルレベルモデルのプロット)
5. 推論データの保存
pickle で MCMCサンプリングデータ idata2 を保存できます。
### 推論データの保存
file = r'idata2_ch3.pkl'
with open(file, 'wb') as f:
pickle.dump(idata2, f)次のコードで保存したファイルを読み込みできます。
### 推論データの読み込み
file = r'idata2_ch3.pkl'
with open(file, 'rb') as f:
idata2_ch3_load = pickle.load(f)モデル3:対数正規分布モデル
1. モデル数式
観測モデルに手が加わります。
年輪幅は正の値であることと、最初の時系列プロットを見ると観測値が大きな値のところで変動が大きくなっていることから、観測値の従う分布を正規分布(負の値もあり)から対数正規分布に変えてみよう、という流れです。
モデル2の2次のトレンドモデルの観測モデルを変更して、次の式のようにします。
$$
\begin{align*}
\alpha_t &= 2\alpha_{t-1} - \alpha_{t-2} + \eta_{t} , \quad \epsilon_t \sim \text{Normal}\ (0,\ \sigma^2_{\epsilon}) \\
y_t &\sim \text{LogNormal}\ (\alpha_t + \sigma^2_{\epsilon}) \\
\end{align*}
$$
1行目は観測モデル(測定方程式)、2行目はシステムモデル(状態方程式)です。
2. モデルの定義
数式モデルに準拠してPyMCのモデルを定義しましょう。
モデル2の尤度関数の確率分布が対数正規分布に変わります。
### モデルの定義
with pm.Model() as model3:
### データ関連定義
# coordの定義
model3.add_coord('data', values=data1.index, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data1['年輪幅'].values, dims='data')
### 事前分布
sigmaEta = pm.Uniform('sigmaEta', lower=0, upper=100)
sigmaEpsilon = pm.Uniform('sigmaEpsilon', lower=0, upper=100)
### システムモデル
init_dist = pm.Uniform.dist(lower=0, upper=10)
alpha = pm.AR('alpha', rho=[2, -1], sigma=sigmaEta, constant=False,
init_dist=init_dist, ar_order=2, dims='data')
### 尤度:観測モデル
Y = pm.LogNormal('Y', mu=alpha, sigma=sigmaEpsilon, observed=y, dims='data')モデルの内容を表示・可視化してみましょう。
### モデルの表示
model3【実行結果】

続いてモデルを可視化します。
### モデルの可視化
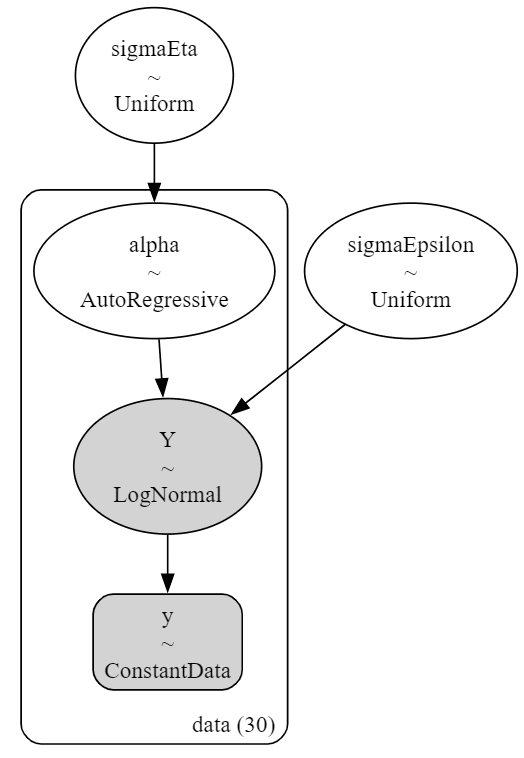
pm.model_to_graphviz(model3)【実行結果】
下から2番目の Y の確率分布が変わりました。
3. MCMCの実行と収束の確認
■ MCMC
マルコフ連鎖=chainsを4本、バーンイン期間=tuneを1000、利用するサンプル=drawを1chainあたり1000に設定して、合計4000個の事後分布からのサンプリングデータを生成します。テキストの指定数とは異なっています。
サンプル方法に numpyro を指定しています。処理速度が早くなります。
numpyro を使わない場合は「nuts_sampler='numpyro',」を削除します。
### 事後分布からのサンプリング 20秒
with model3:
idata3 = pm.sample(draws=1000, tune=1000, chains=4, random_seed=123,
nuts_sampler='numpyro', target_accept=0.999)【実行結果】
処理時間は20秒です。

■ $${\hat{R}}$$で収束確認
収束の確認をします。
指標$${\hat{R}}$$(あーるはっと)の値が$${1.1}$$以下のとき、収束したこととします。
上記基準を超える個数が0ならば、$${\hat{R} \leq1.1}$$なので収束したとみなします。
### r_hat>1.1の確認
# 設定
idata_in = idata3 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R}>1.1}$$のパラメータは0個でした。
$${\hat{R} \leq1.1}$$なので収束したとみなします。

■ $${\hat{R}}$$の値把握と事後統計量の表示
### 事後統計量の表示
var_names = ['sigmaEpsilon', 'sigmaEta', 'alpha']
pm.summary(idata3, hdi_prob=0.95, var_names=var_names)【実行結果】
対数をとる関係でパラメータの事後分布の値が大きく変わったようです。

■ トレースプロットで収束確認
トレースプロットを描画します。
こちらの図でも収束の確認を行えます。
### トレースプロットの描画
pm.plot_trace(idata3, compact=True, var_names=var_names)
plt.tight_layout();【実行結果】
左プロットの線の重なり具合、右プロットの偏りのない乱雑さより、収束している感じがします。
ただ、グラフの下に見えるバーコードのような線で「発散」しているデータがあることが示されています。
発散はいい状態では無いことを意味します。

4. 分析
状態$${\alpha}$$の事後分布を描画しましょう。
テキストの図5に相当します。
$${\alpha}$$は対数スケールになっているので、指数関数$${\exp}$$で観測値のスケールに変換します。
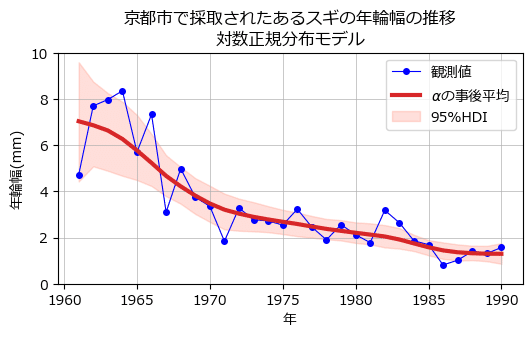
### 観測ノイズを対数正規分布とした2次トレンドモデルによる例 ※図5に相当
## 描画用データの作成
# 事後分布サンプリングデータからαを取り出して指数を取る
alpha_samples = np.exp(idata3.posterior.alpha.
stack(sample=('chain', 'draw')).data)
# 年輪幅の期待値αの事後平均を算出
alpha_means = alpha_samples.mean(axis=1)
# 年輪幅の期待値αの95%HDIを算出
alpha_95hdi = az.hdi(alpha_samples.T).T
## 描画
fig, ax = plt.subplots(figsize=(6, 3))
# 観測値の折れ線グラフ
ax.plot(data1, '-o', markersize=4, color='blue', lw=0.8, label='観測値')
# αの事後平均の折れ線グラフ
ax.plot(data1.index, alpha_means, color='tab:red', lw=3,
label=r'$\alpha$の事後平均')
# αの95%HDIを塗りつぶし
ax.fill_between(data1.index, alpha_95hdi[0], alpha_95hdi[1], color='tomato',
alpha=0.2, label='95%HDI')
# 修飾
ax.set(xlabel='年', ylabel='年輪幅(mm)', ylim=(0, 10),
title='京都市で採取されたあるスギの年輪幅の推移\n対数正規分布モデル')
ax.grid(lw=0.5)
ax.legend();【実行結果】
赤い線が$${\alpha}$$の事後分布の平均値、ピンクの面が$${\alpha}$$の95%HDI区間です。
事後平均の赤い線がますます滑らかになり、直線に近づいている感じがします。
また、年輪幅が小さくなるにつれて95%HDIの幅が狭くなっています。
(右になるほどピンク面が細くなっています)
(参考:2次トレンドモデル)

(参考:ローカルレベルモデルのプロット)
システムモデルのレベル、トレンドの表現や、観測モデルの確率分布の表現によって、得られる事後分布が変わることがよく分かりました。
5. 推論データの保存
pickle で MCMCサンプリングデータ idata3 を保存できます。
### 推論データの保存
file = r'idata3_ch3.pkl'
with open(file, 'wb') as f:
pickle.dump(idata3, f)次のコードで保存したファイルを読み込みできます。
### 推論データの読み込み
file = r'idata3_ch3.pkl'
with open(file, 'rb') as f:
idata3_ch3_load = pickle.load(f)ベイズ記事は以上です。
次回予告
「時系列・空間データのモデリング」章
状態空間モデル「野生の鳥のカウントデータ」
結び
今回の取組みは、状態空間モデルによる時系列データの基礎を学び・復習するのに程よいレベル感だと思います。
何度も見返したいと思います。
おわり
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
