
第15章「探すのに集中しているときとそうでないときで何が違うのか?」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング」の第15章「探すのに集中しているときとそうでないときで何が違うのか?」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、何かを探して見つけるまでの時間を異なる2つのシーンで実験して、シーンによる違いをベイズモデリングで推論します。
今回のモデルはそれほど複雑では無いのですが、どうしても収束に至ることができませんでした(汗)
私はPyMCの「指数-正規分布」クラスを使いこなせていないようです・・・。

何とかして結果を探して見つけられるようにと、記事では4つのモデルを試しています。
PyMCモデリングで試行錯誤することも、ベイズ実践の楽しみです!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 井上和哉 先生
モデル難易度: ★★★・・ (ふつう)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★・・・& いまいち \\
結果再現度 & ★★・・・& やや悪い \\
楽しさ & ★★★★★& 楽しい! \\
\end{array}
$$

評価ポイント
テキストのモデルを再現できず、分布は収束しませんでした。
工夫・喜び・反省
全然収束しない苦しさを噛み締めた章でした。
ただ指をくわえて見ているだけでは癪なので、この際、やりたいことをやろうと割り切って、ちょっぴり悪あがきしてみました。
モデルの概要
テキストの調査・実験の概要
■探索メインブロックと記憶メインブロック
10名の実験参加者による「ミニカー画像の探索時間」を分析するのがテキストの実験の主旨になります。
ただ探すのではなく、次の2つのシーン:ブロックを意図的に作り出して、探索時間を計測しています。
① 探索メインブロック
192試行に探索課題、48試行に記憶課題を用いた「探索課題」メインの実験です。
探索課題は、コンピュータ画面に映し出されたミニカーを探し、右向きか左向きかを報告します。
記憶課題は、コンピュータ画面の画像の一部が変化したかどうかを報告します。
探索課題と記憶課題はランダムに表示されます。

② 記憶メインブロック
192試行に記憶課題、48試行に探索課題を用いた「記憶課題」メインの実験です。
テキストでは、探索課題の探索時間=反応時間が、探索メインブロックの方が短く、記憶メインブロックの方が長くなることを想定して、ブロック間で反応時間の何が異なるのかを分析するとされています。
実験の概要を図示します。

テキストのモデリング
■目的変数と関心のあるパラメータ
目的変数$${RT_{ij}}$$は探索課題の反応時間(秒)です。
関心事は、集団レベルで探索メインブロックと記憶メインブロックのパラメータに意味のある差があるかどうかです。
■指数-正規分布を用いた階層モデル
反応時間$${RT_{ij}}$$は指数-正規分布に従うとしています。
添字$${i}$$は実験参加者のID、$${j}$$はブロック条件であり、$${j=s}$$は探索メインブロック、$${j=m}$$は記憶メインブロックです。
指数-正規分布の3つのパラメータ$${\mu_{ij},\ \sigma_{ij},\ \lambda_{ij}}$$は、2変量正規分布に従うとしています。
$$
\begin{align*}
RT_{ij} &\sim \text{ExGaussian}\ (\mu_{ij},\ \sigma_{ij},\ \lambda_{ij}) \\
\left( \begin{matrix} \mu_{im} \\ \mu_{is}\end{matrix} \right) &\sim \text{multiNormal}\ \left(\left( \begin{matrix} mean_{\mu_m} \\ mean_{\mu_s}\end{matrix}\right), \left( \begin{matrix} var_{\mu_m} & cov_{\mu_m \mu_s} \\ cov_{\mu_m \mu_s } & var_{\mu_s}\end{matrix}\right) \right) \\
\left( \begin{matrix} \sigma_{im} \\ \sigma_{is}\end{matrix} \right) &\sim \text{multiNormal}\ \left(\left( \begin{matrix} mean_{\sigma_m} \\ mean_{\sigma_s}\end{matrix}\right), \left( \begin{matrix} var_{\sigma_m} & cov_{\sigma_m \sigma_s} \\ cov_{\sigma_m \sigma_s } & var_{\sigma_s}\end{matrix}\right) \right) \\
\left( \begin{matrix} \lambda_{im} \\ \lambda_{is}\end{matrix} \right) &\sim \text{multiNormal}\ \left(\left( \begin{matrix} mean_{\lambda_m} \\ mean_{\lambda_s}\end{matrix}\right), \left( \begin{matrix} var_{\lambda_m} & cov_{\lambda_m \lambda_s} \\ cov_{\lambda_m \lambda_s } & var_{\lambda_s}\end{matrix}\right) \right) \\
\end{align*}
$$
2変量正規分布の平均$${mean}$$と分散$${var}$$は範囲$${[ 0,\ \infty]}$$の一様分布、共分散$${cov}$$算出に利用する相関係数$${\rho}$$は範囲$${[ -1,\ 1]}$$の一様分布に従うとしています。
■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルは収束できず、分析に利用できない状況です。

PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
# 数値・確率計算
import pandas as pd
import numpy as np
from scipy.stats import exponnorm
import pingouin as pg
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込みと前処理
csvファイルをpandasのデータフレームに読み込みます。
あわせて、テキストのRコードと同様の前処理(外れ値除去)を実施します。
### データの読み込み
# データの読み込み
# rtは反応時間、subは参加者ID、cond=1は探索メインブロック、2は記憶メインブロック
data = pd.read_csv('search_rt.csv')
# 反応時間rt が0.2秒以下、または、15秒以上の試行50個は外れ値として除外
data = data[~((data['rt']<=0.2) | (data['rt']>=15))].reset_index()
# データの表示
print('オリジナル: ', data.shape)
print('外れ値除外: ', data.shape)
display(data)【実行結果】
全2350行です。
データ項目は次のとおりです。
・rt:反応時間(秒)
・sub:実験参加者のID
・cond:探索メインブロックは1、記憶メインブロックは2

3.指数-正規分布の形状
指数-正規分布の3つのパラメータ$${\mu, \sigma, \lambda}$$の値を変化させて、指数-正規分布の確率密度関数の形状を確認します。
テキストの図15.1に相当します。
指数-正規分布は scipy.stats の exponnorm 関数で対応できます。
### 指数-正規分布のパラメータと形状の関係を描画 ※図15.1に相当
# scipy.statsのexponnormを利用 パラメータK=1/(σλ)
## 初期値設定
# 指数-正規分布のパラメータリスト:μ、σ、λの順にセット
params = [[[0.5, 0.1, 2.0], [1.0, 0.1, 2.0], [1.5, 0.1, 2.0]],
[[0.8, 0.1, 2.0], [0.8, 0.3, 2.0], [0.8, 0.7, 2.0]],
[[0.8, 0.1, 1.0], [0.8, 0.1, 2.0], [0.8, 0.1, 3.0]],
[[0.5, 0.1, 1.0], [1.0, 0.1, 2.0]]]
# 線の色と形状
colors = ['tab:blue', 'tab:green', 'tab:red']
styles = ['-', '--', ':']
# 凡例
labels = [[r'$\mu$=0.5', r'$\mu$=1.0', r'$\mu$=1.5'],
[r'$\sigma$=0.1', r'$\sigma$=0.3', r'$\sigma$=0.7'],
[r'$\lambda$=1.0', r'$\lambda$=2.0', r'$\lambda$=3.0'],
[r'$\mu$=0.5, $\sigma$=0.1, $\lambda$=1.0',
r'$\mu$=1.0, $\sigma$=0.1, $\lambda$=2.0']]
# グラフタイトル
titles1 = ['A', 'B', 'C', 'D']
titles2 = [r'$\sigma$=0.1, $\lambda$=2.0', r'$\mu$=0.8, $\lambda$=2.0',
r'$\mu$=0.8, $\sigma$=0.1', '']
# x座標配列の設定
x = np.linspace(0, 4, 1001)
## 描画
fig, axes = plt.subplots(2, 2, figsize=(7, 7), sharex=True, sharey=True)
# 4つのグラフを繰り返し描画
for i, ax in enumerate(axes.flatten()):
# 1つのグラフの複数曲線を繰り返し描画
for j, param in enumerate(params[i]):
# scipy.statsのexponnormで指数-正規分布の確率密度関数の値を算出
y = exponnorm.pdf(x, K=1/(param[1]*param[2]), loc=param[0],
scale=param[1])
# 指数-正規分布の確率密度関数を描画
ax.plot(x, y, ls=styles[j], color=colors[j], label=labels[i][j])
# タイトルとy軸範囲を設定
ax.set(title=f'{titles1[i]} : {titles2[i]}', ylim=(0, 2),
yticks=(0, 0.5, 1, 1.5, 2))
ax.legend()
# グラフ全体の修飾
fig.supxlabel('反応時間(秒)')
fig.supylabel('確率密度')
plt.tight_layout()
plt.show()【実行結果】
指数-正規分布の形状は、左側(下側)に峰が偏り、右側(上側)に裾が長くなっています。
PyMCモデリングでこのような分布を目指します。

4.データの統計量・形状の確認
テキスト15.3節に記載の探索メインブロック・記憶メインブロックの反応時間の平均値、および、対応のある2つの平均の$${t}$$検定を行います。
$${t}$$検定には pingouin の ttest 利用します。
pingouin は統計分野の一部機能に特化した「痒いところに手が届く」系のパッケージです。重宝する優れものです🐧
### 探索メインブロックと記憶メインブロックの平均・標準偏差・対応のあるt検定
# ブロック(cond)・参加者(sub)別の反応時間の平均値の計算
data_mean = data.groupby(['cond', 'sub'])['rt'].mean().reset_index()
print('【探索メインブロック(cond=1)と記憶メインブロック(cond=2)の平均・標準偏差】')
display(data_mean.groupby(['cond'])['rt'].agg(['mean', 'std']).round(2))
# 対応のある2標本の母平均のt検定
print('【対応のある2標本の母平均のt検定】')
pg.ttest(data_mean[data_mean['cond']==2]['rt'],
data_mean[data_mean['cond']==1]['rt'],
paired=True, alternative='two-sided', correction=False)【実行結果】
$${p}$$値(p-val)は$${0.000}$$です。
有意水準$${5\%}$$で各ブロックの平均反応時間は差があると言えるでしょう。
テキストでは探索メインブロックの反応時間が有意に短いとしています。

続いて、記憶メインブロックと探索メインブロックのヒストグラムを確認します。
テキストの図15.3に相当します。
### 記憶メインブロックと探索メインブロックのヒストグラムの描画 ※図15.3に相当
fig, ax = plt.subplots(1, 2, figsize=(7, 4), sharex=True, sharey=True)
# 記憶メインブロックのヒストグラムの描画
ax[0].hist(data[data['cond']==2]['rt'], bins=30, density=True)
ax[0].set(title='記憶メインブロック', xticks=(0, 5, 10, 15))
# 探索メインブロックのヒストグラムの描画
ax[1].hist(data[data['cond']==1]['rt'], bins=30, density=True)
ax[1].set(title='探索メインブロック')
# 全体の修飾
fig.supxlabel('反応時間(秒)')
fig.supylabel('確率密度')
plt.tight_layout()
plt.show()【実行結果】
ヒストグラムは左側(下側)に偏っており、右側(上側)の裾が長い形状です。正規分布のベル型をしていません。
テキストは「指数-正規分布」の利用が適しているとしています。


モデル構築
モデルの数式表現
PyMCの指数-正規分布クラス(と思われる)「ExGaussian」を利用します。
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\begin{align*}
\mu &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\mu_{\sigma_{search}} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\mu_{\sigma_{memory}} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\mu_{\rho} &\sim \text{Uniform}\ (\text{lower}=-1,\ \text{upper}=1) \\
\mu_{cov} &= \left[\begin{matrix} \mu_{\sigma_{search}}^2 & \mu_{\sigma_{search}} \times \mu_{\sigma_{memory}} \times \mu_{\rho} \\ \mu_{\sigma_{search}} \times \mu_{\sigma_{memory}} \times \mu_{\rho} & \mu_{\sigma_{memory}}^2 \end{matrix} \right] \\
\mu_{ind} &\sim \text{MvNormal}\ (\text{mu}=\mu,\ \text{cov}=\mu_{cov}) \\
\\
\sigma &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\sigma_{\sigma_{search}} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\sigma_{\sigma_{memory}} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\sigma_{\rho} &\sim \text{Uniform}\ (\text{lower}=-1,\ \text{upper}=1) \\
\sigma_{cov} &= \left[\begin{matrix} \sigma_{\sigma_{search}}^2 & \sigma_{\sigma_{search}} \times \sigma_{\sigma_{memory}} \times \sigma_{\rho} \\ \sigma_{\sigma_{search}} \times \sigma_{\sigma_{memory}} \times \sigma_{\rho} & \sigma_{\sigma_{memory}}^2 \end{matrix} \right] \\
\sigma_{ind} &\sim \text{MvNormal}\ (\text{mu}=\sigma,\ \text{cov}=\sigma_{cov}) \\
\\
\nu &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\nu_{\sigma_{search}} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\nu_{\sigma_{memory}} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\nu_{\rho} &\sim \text{Uniform}\ (\text{lower}=-1,\ \text{upper}=1) \\
\nu_{cov} &= \left[\begin{matrix} \nu_{\sigma_{search}}^2 & \nu_{\sigma_{search}} \times \nu_{\sigma_{memory}} \times \nu_{\rho} \\ \nu_{\sigma_{search}} \times \nu_{\sigma_{memory}} \times \nu_{\rho} & \nu_{\sigma_{memory}}^2 \end{matrix} \right] \\
\nu_{ind} &\sim \text{MvNormal}\ (\text{mu}=\nu,\ \text{cov}=\nu_{cov}) \\
\\
lilelihood &\sim \text{ExGaussian}\ (\text{mu}=\mu_{ind},\ \text{sigma}=\sigma_{ind},\ \text{nu}=\nu_{ind})\\
\end{align*}
$$
1.モデルの定義
参加者ID sub と条件 cond は0始まりになるようにデータを変形します。
また、登場する確率変数が多いので、モデルの数式も多くなりました。
巻絵のような長~いモデルです。
### モデルの定義
# 初期値設定
idx_sub = list(data['sub'].values - 1) # 参加者ID(0始まりに変更)
idx_cond = list(data['cond'].values - 1) # メインブロック(0:探索、1:記憶)
# モデルの定義
with pm.Model() as model:
### データ関連定義
# coordの定義
model.add_coord('data', values=data.index, mutable=True)
model.add_coord('sub', values=data['sub'].unique(), mutable=True)
model.add_coord('cond', values=['探索', '記憶'], mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data['rt'].values, dims='data')
subIdx = pm.ConstantData('subIdx', value=idx_sub, dims='data')
condIdx = pm.ConstantData('condIdx', value=idx_cond, dims='data')
### 事前分布
## μ:指数-正規分布の正規分布側の平均パラメータ
# mu:集団レベル
mu = pm.Uniform('mu', lower=0, upper=100, dims='cond')
# cov matrix
muSigmaSea = pm.Uniform('muSigmaSea', lower=0, upper=100) # 探索
muSigmaMem = pm.Uniform('muSigmaMem', lower=0, upper=100) # 記憶
muRho = pm.Uniform('muRho', lower=-1, upper=1) # 相関係数
muCovMtx = pm.Deterministic('muCovMtx',
pt.stacklists([[pt.pow(muSigmaSea, 2), muSigmaSea*muSigmaMem*muRho],
[muSigmaSea*muSigmaMem*muRho, pt.pow(muSigmaMem, 2)]]))
# muInd:多変量正規分布・個人レベル
muInd = pm.MvNormal('muInd', mu=mu, cov=muCovMtx, dims=('sub', 'cond'))
## σ:指数-正規分布の正規分布側の標準偏差パラメータ
# sigma:集団レベル
sigma = pm.Uniform('sigma', lower=0, upper=100, dims='cond')
# cov matrix
sigmaSigmaSea = pm.Uniform('sigmaSigmaSea', lower=0, upper=100) # 探索
sigmaSigmaMem = pm.Uniform('sigmaSigmaMem', lower=0, upper=100) # 記憶
sigmaRho = pm.Uniform('sigmaRho', lower=-1, upper=1) # 相関係数
sigmaCovMtx = pm.Deterministic('sigmaCovMtx',
pt.stacklists(
[[pt.pow(sigmaSigmaSea, 2), sigmaSigmaSea*sigmaSigmaMem*sigmaRho],
[sigmaSigmaSea*sigmaSigmaMem*sigmaRho, pt.pow(sigmaSigmaMem, 2)]]))
# sigmaInd:多変量正規分布・個人レベル
sigmaInd = pm.MvNormal('sigmaInd', mu=sigma, cov=sigmaCovMtx,
dims=('sub', 'cond'))
## ν:指数-正規分布の指数分布側のパラメータ
# nu:集団レベル
nu = pm.Uniform('nu', lower=0, upper=100, dims='cond')
# cov matrix
nuSigmaSea = pm.Uniform('nuSigmaSea', lower=0, upper=100) # 探索
nuSigmaMem = pm.Uniform('nuSigmaMem', lower=0, upper=100) # 記憶
nuRho = pm.Uniform('nuRho', lower=-1, upper=1) # 相関係数
nuCovMtx = pm.Deterministic('nuCovMtx',
pt.stacklists(
[[pt.pow(nuSigmaSea, 2), nuSigmaSea*nuSigmaMem*nuRho],
[nuSigmaSea*nuSigmaMem*nuRho, pt.pow(nuSigmaMem, 2)]]))
# nuInd:多変量正規分布・個人レベル
nuInd = pm.MvNormal('nuInd', mu=nu, cov=nuCovMtx, dims=('sub', 'cond'))
### 尤度:指数-正規分布
likelihood = pm.ExGaussian('likelihood',
mu=muInd[subIdx, condIdx],
sigma=sigmaInd[subIdx, condIdx],
nu=nuInd[subIdx, condIdx],
observed=y, dims='data')
### 計算
# lamの算出 λ=1/ν
lamInd = pm.Deterministic('lamInd', 1/nuInd, dims=('sub', 'cond'))
lam = pm.Deterministic('lam', 1/nu, dims='cond')
# 集団レベルのμ、σ、λ、νについて、記憶と探索の差分
muDiff = pm.Deterministic('muDiff', mu[1] - mu[0])
sigmaDiff = pm.Deterministic('sigmaDiff', sigma[1] - sigma[0])
lamDiff = pm.Deterministic('lamDiff', lam[1] - lam[0])
nuDiff = pm.Deterministic('nuDiff', nu[1] - nu[0])【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の3つを設定しました。
・行の座標:名前「data」、値「行インデックス」
・実験参加者IDの座標:名前「sub」、値「参加者ID-1」
・条件の座標:名前「cond」、値「探索、記憶」dataの定義
目的変数$${y}$$、実験参加者IDインデックス$${subIdx}$$、条件インデックス$${subIdx}$$を設定しました。パラメータの事前分布
テキストにならって設定しました。
なお、一様分布の範囲$${[0,\ \infty]}$$は$${[0,\ 100]}$$に変更しています。$${\lambda}$$の扱い
PyMCの指数-正規分布(と思われる)ExGaussian()のパラメータは$${\nu}$$はおそらく$${1/\lambda}$$だろうと推測しました。
そこで、$${\lambda}$$は計算値の箇所で再計算するようにしました。
尤度
個人パラメータである$${\mu_{ind}}$$、$${\sigma_{ind}}$$、$${\nu_{ind}}$$をパラメータにする指数-正規分布に従います。
2.モデルの外観の確認
### モデルの表示
model【実行結果】
長いですね。。。
次のモデル構造図はきっと絵巻物でしょう。

### モデルの可視化
pm.model_to_graphviz(model)【実行結果】
巨大で横に長~いモデルです!

3.事後分布からのサンプリング
乱数生成数はテキストと合わせています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ61分でした。
# 事後分布からのサンプリング 61分
with model:
idata = pm.sample(draws=12000, tune=1000, chains=4, target_accept=0.99,
nuts_sampler='numpyro', random_seed=123)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
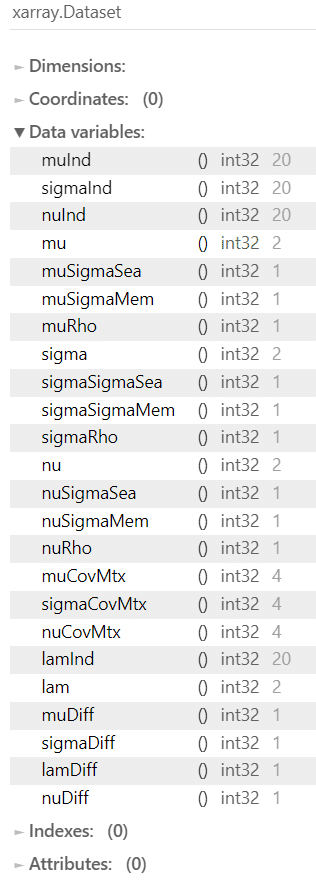
(rhat_idata > 1.1).sum()【実行結果】
下の図の値は20、20、20・・・と0になる気配が無いです。
まったく収束しません・・・(汗)
試しに事後分布のサンプリングデータから、集団レベルのパラメータの推定値を確認します。
テキストの表15.1に相当します。
### 推論データの要約統計情報の表示 集団レベル
var_names = ['mu', 'sigma', 'lam']
pm.summary(idata, hdi_prob=0.95, var_names=var_names).round(3)【実行結果】
事後分布の平均値 mean はテキストのEAPと1~2桁相違します。
どうしてこんな結果に・・・。

実は、パラメータの事前分布に用いる「一様分布」の上限を100→10→1へと小さくすると、上述の事後分布サンプリングデータの推定値の値も小さくなります。
モデル記述内容におかしな点があるのでしょう。
(しかし、問題点を見つけることはできませんでした。)


おまけモデル1
何となくですが、尤度関数「指数-正規分布」の「指数」の部分をうまく設定できていない感じがします。
そこで、「指数」を抜いて「正規分布」でモデリングしてみます。
なおヒストグラムの形状の通り、反応時間データは正規分布とは異なる形状なので、正規分布によるモデリングの推論値はデータの気持ちを汲み取っていない結果になることを予めお断りします。
1.モデルの定義
尤度関数「likelihood」を pm.Normal() にしました。
また、正規分布に関係のないパラメータ$${\nu}$$、$${\lambda}$$にかかる変数を削除しました。
### モデルの定義
# 初期値設定
idx_sub = list(data['sub'].values - 1) # 参加者ID(0始まりに変更)
idx_cond = list(data['cond'].values - 1) # メインブロック(0:探索、1:記憶)
# モデルの定義
with pm.Model() as model:
### データ関連定義
# coordの定義
model.add_coord('data', values=data.index, mutable=True)
model.add_coord('sub', values=data['sub'].unique(), mutable=True)
model.add_coord('cond', values=['探索', '記憶'], mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data['rt'].values, dims='data')
subIdx = pm.ConstantData('subIdx', value=idx_sub, dims='data')
condIdx = pm.ConstantData('condIdx', value=idx_cond, dims='data')
### 事前分布
## μ:指数-正規分布の正規分布側の平均パラメータ
# mu:集団レベル
mu = pm.Uniform('mu', lower=0, upper=100, dims='cond')
# cov matrix
muSigmaSea = pm.Uniform('muSigmaSea', lower=0, upper=100) # 探索
muSigmaMem = pm.Uniform('muSigmaMem', lower=0, upper=100) # 記憶
muRho = pm.Uniform('muRho', lower=-1, upper=1) # 相関係数
muCovMtx = pm.Deterministic('muCovMtx',
pt.stacklists([[pt.pow(muSigmaSea, 2), muSigmaSea*muSigmaMem*muRho],
[muSigmaSea*muSigmaMem*muRho, pt.pow(muSigmaMem, 2)]]))
# muInd:多変量正規分布・個人レベル
muInd = pm.MvNormal('muInd', mu=mu, cov=muCovMtx, dims=('sub', 'cond'))
## σ:指数-正規分布の正規分布側の標準偏差パラメータ
# sigma:集団レベル
sigma = pm.Uniform('sigma', lower=0, upper=100, dims='cond')
# cov matrix
sigmaSigmaSea = pm.Uniform('sigmaSigmaSea', lower=0, upper=100) # 探索
sigmaSigmaMem = pm.Uniform('sigmaSigmaMem', lower=0, upper=100) # 記憶
sigmaRho = pm.Uniform('sigmaRho', lower=-1, upper=1) # 相関係数
sigmaCovMtx = pm.Deterministic('sigmaCovMtx',
pt.stacklists(
[[pt.pow(sigmaSigmaSea, 2), sigmaSigmaSea*sigmaSigmaMem*sigmaRho],
[sigmaSigmaSea*sigmaSigmaMem*sigmaRho, pt.pow(sigmaSigmaMem, 2)]]))
# sigmaInd:多変量正規分布・個人レベル
sigmaInd = pm.MvNormal('sigmaInd', mu=sigma, cov=sigmaCovMtx,
dims=('sub', 'cond'))
### 尤度:正規分布にすると収束する
likelihood = pm.Normal('likelihood',
mu=muInd[subIdx, condIdx],
sigma=sigmaInd[subIdx, condIdx],
observed=y, dims='data')
### 計算
# 集団レベルのμ、σ、λ、νについて、記憶と探索の差分
muDiff = pm.Deterministic('muDiff', mu[1] - mu[0])
sigmaDiff = pm.Deterministic('sigmaDiff', sigma[1] - sigma[0])【実行結果】なし
2.モデルの外観の確認
### モデルの表示
model【実行結果】

### モデルの可視化
pm.model_to_graphviz(model)【実行結果】

3.事後分布からのサンプリング
乱数生成数は tune を多めにしました。
また、target_accept の値を大きくしました。
NUTSサンプラーに numpyro を利用して、処理時間はおよそ10分でした。
# 事後分布からのサンプリング 10分
with model:
idata = pm.sample(draws=12000, tune=8000, chains=4, target_accept=0.998,
nuts_sampler='numpyro', random_seed=123)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
(rhat_idata > 1.1).sum()【実行結果】
なんと!$${\hat{R} \leq 1.1}$$です!収束しています!


4.事後予測
モデルの当てはまり具合を目的変数の事後予測データで確認します。
### 事後予測サンプリング
with model:
idata.extend(pm.sample_posterior_predictive(idata, random_seed=123))【実行結果】

### 事後予測のプロット
fig, ax = plt.subplots(figsize=(10, 4))
pm.plot_ppc(idata, num_pp_samples=100, random_seed=123, ax=ax)
ax.set(xlabel='反応時間(秒)', ylabel='density', title='事後予測プロット');【実行結果】
黒線が観測値の反応時間、オレンジの点線が事後予測値です。
形状は全く異なりますね・・・。
マイナスの反応時間も見られます。
もしかすると切断正規分布(PyMCのTruncatedNormal)の方が良かったかな?(後で試してみます)
確かに、このデータは正規分布で表現しきれないことが理解できました。

5.事後分布サンプリングデータの推定値
一応、パラメータの事後分布の各値を表示してみます。
テキストの表15.1~15.4の正規分布版に相当します。
①集団レベル
### 推論データの要約統計情報の表示 集団レベル
var_names = ['mu', 'sigma']
pm.summary(idata, hdi_prob=0.95, var_names=var_names).round(3)【実行結果】

②個人レベル:記憶メインブロック
「coords={'cond': '記憶'}」を指定することで、変数 cond が「記憶」のデータを抽出できます。
### 推論データの要約統計情報の表示 個人レベル 記憶メインブロック
var_names = ['muInd', 'sigmaInd']
(pm.summary(idata, hdi_prob=0.95, var_names=var_names, coords={'cond': '記憶'})
.round(3))【実行結果】

③個人レベル:探索メインブロック
### 推論データの要約統計情報の表示 個人レベル 探索メインブロック
var_names = ['muInd', 'sigmaInd']
(pm.summary(idata, hdi_prob=0.95, var_names=var_names, coords={'cond': '探索'})
.round(3))【実行結果】

④集団レベルのパラメータの条件差
「記憶-探索」の値です。
### 推論データの要約統計情報の表示 集団レベルの各パラメータの条件差
var_names = ['muDiff', 'sigmaDiff']
pm.summary(idata, hdi_prob=0.95, var_names=var_names).round(3)【実行結果】
平均 mu も標準偏差 sigma も 95%HDIが0以上となっており、記憶メインブロックの方が反応時間が長い様子がわかります。


おまけモデル2
指数分布と正規分布、なんとか混ぜ混ぜして表現できないでしょうか?
混ぜ混ぜ・・・混合!
指数分布と正規分布の混合分布を試してみます!
1.モデルの定義
尤度関数「likelihood」を pm.Mixture() にしました。
### モデルの定義
# 初期値設定
idx_sub = list(data['sub'].values - 1) # 参加者ID(0始まりに変更)
idx_cond = list(data['cond'].values - 1) # メインブロック(0:探索、1:記憶)
# モデルの定義
with pm.Model() as model:
### データ関連定義
# coordの定義
model.add_coord('data', values=data.index, mutable=True)
model.add_coord('sub', values=data['sub'].unique(), mutable=True)
model.add_coord('cond', values=['探索', '記憶'], mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data['rt'].values, dims='data')
subIdx = pm.ConstantData('subIdx', value=idx_sub, dims='data')
condIdx = pm.ConstantData('condIdx', value=idx_cond, dims='data')
### 事前分布
## μ:指数-正規分布の正規分布側の平均パラメータ
# mu:集団レベル
mu = pm.Uniform('mu', lower=0, upper=100, dims='cond')
# cov matrix
muSigmaSea = pm.Uniform('muSigmaSea', lower=0, upper=100) # 探索
muSigmaMem = pm.Uniform('muSigmaMem', lower=0, upper=100) # 記憶
muRho = pm.Uniform('muRho', lower=-1, upper=1) # 相関係数
muCovMtx = pm.Deterministic('muCovMtx',
pt.stacklists([[pt.pow(muSigmaSea, 2), muSigmaSea*muSigmaMem*muRho],
[muSigmaSea*muSigmaMem*muRho, pt.pow(muSigmaMem, 2)]]))
# muInd:多変量正規分布・個人レベル
muInd = pm.MvNormal('muInd', mu=mu, cov=muCovMtx, dims=('sub', 'cond'))
## σ:指数-正規分布の正規分布側の標準偏差パラメータ
# sigma:集団レベル
sigma = pm.Uniform('sigma', lower=0, upper=100, dims='cond')
# cov matrix
sigmaSigmaSea = pm.Uniform('sigmaSigmaSea', lower=0, upper=100) # 探索
sigmaSigmaMem = pm.Uniform('sigmaSigmaMem', lower=0, upper=100) # 記憶
sigmaRho = pm.Uniform('sigmaRho', lower=-1, upper=1) # 相関係数
sigmaCovMtx = pm.Deterministic('sigmaCovMtx',
pt.stacklists(
[[pt.pow(sigmaSigmaSea, 2), sigmaSigmaSea*sigmaSigmaMem*sigmaRho],
[sigmaSigmaSea*sigmaSigmaMem*sigmaRho, pt.pow(sigmaSigmaMem, 2)]]))
# sigmaInd:多変量正規分布・個人レベル
sigmaInd = pm.MvNormal('sigmaInd', mu=sigma, cov=sigmaCovMtx,
dims=('sub', 'cond'))
lam = pm.Uniform('lam', lower=0, upper=100, dims='cond')
# cov matrix
lamSigmaSea = pm.Uniform('lamSigmaSea', lower=0, upper=100) # 探索
lamSigmaMem = pm.Uniform('lamSigmaMem', lower=0, upper=100) # 記憶
lamRho = pm.Uniform('lamRho', lower=-1, upper=1) # 相関係数
lamCovMtx = pm.Deterministic('lamCovMtx',
pt.stacklists(
[[pt.pow(lamSigmaSea, 2), lamSigmaSea*lamSigmaMem*lamRho],
[lamSigmaSea*lamSigmaMem*lamRho, pt.pow(lamSigmaMem, 2)]]))
# lamInd:多変量正規分布・個人レベル
lamInd = pm.MvNormal('lamInd', mu=lam, cov=lamCovMtx, dims=('sub', 'cond'))
### 尤度:正規分布と指数分布の混合分布
# 混合比率
w = pm.Dirichlet('w', a=np.array([1, 1]))
# 分布の構成
components = [pm.Normal.dist(mu=muInd[subIdx, condIdx],
sigma=sigmaInd[subIdx, condIdx]),
pm.Exponential.dist(lam=lamInd[subIdx, condIdx])]
# 尤度 混合分布
likelihood = pm.Mixture('likelihood', w=w, comp_dists=components,
observed=y, dims='data')
### 計算
# 集団レベルのμ、σ、λ、νについて、記憶と探索の差分
muDiff = pm.Deterministic('muDiff', mu[1] - mu[0])
sigmaDiff = pm.Deterministic('sigmaDiff', sigma[1] - sigma[0])
lamDiff = pm.Deterministic('lamDiff', lam[1] - lam[0])【実行結果】なし
【モデル補足】
混合分布 Mixture() の要素は 混合する分布 comp_dist と 混合比率 w です。
混合する分布は components で 正規分布 Nomal.dist() と 指数分布 Exponential.dist() を指定しました。
混合比率は w で ディリクレ分布(確率の合計が1になる)を利用しました。
2.モデルの外観の確認
### モデルの表示
model【実行結果】

### モデルの可視化
pm.model_to_graphviz(model)【実行結果】

3.事後分布からのサンプリング
乱数生成数は tune を多めにしました。
また、target_accept の値を大きくしました。
NUTSサンプラーに numpyro を利用して、処理時間はおよそ2時間30分でした(のぞみ🚅東京・大阪間・・・)
# 事後分布からのサンプリング 2時間28分30秒
with model:
idata = pm.sample(draws=12000, tune=8000, chains=4, target_accept=0.99,
nuts_sampler='numpyro', random_seed=123)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
(rhat_idata > 1.1).sum()【実行結果】
収束しませんでした・・・。
指数は鬼門かもです・・・。

4.事後予測
ひとまず事後予測の形状を見てみましょう。
### 事後予測サンプリング 11分20秒
with model:
idata.extend(pm.sample_posterior_predictive(idata, random_seed=123))【実行結果】
処理時間はおよそ11分。

### 事後予測のプロット
fig, ax = plt.subplots(figsize=(10, 4))
pm.plot_ppc(idata, num_pp_samples=100, random_seed=123, ax=ax)
ax.set(xlabel='反応時間(秒)', ylabel='density', title='事後予測プロット');【実行結果】
黒線が観測値の反応時間、オレンジの点線が事後予測値です。
正規分布モデルよりはいい線の予感です。
ただ、$${-10}$$や$${50}$$超のデータが見られる区間幅の広い推論になりました。


おまけモデル3
先ほど思いついた「切断正規分布」モデルを試してみます!
1.モデルの定義
尤度関数「likelihood」を pm.TruncatedNormal() にしました。
切断する下限値は lower=0 で設定します。
その他の引数は 通常の正規分布 pm.Normal() と同じです。
### モデルの定義
# 初期値設定
idx_sub = list(data['sub'].values - 1) # 参加者ID(0始まりに変更)
idx_cond = list(data['cond'].values - 1) # メインブロック(0:探索、1:記憶)
# モデルの定義
with pm.Model() as model:
### データ関連定義
# coordの定義
model.add_coord('data', values=data.index, mutable=True)
model.add_coord('sub', values=data['sub'].unique(), mutable=True)
model.add_coord('cond', values=['探索', '記憶'], mutable=True)
# dataの定義
y = pm.ConstantData('y', value=data['rt'].values, dims='data')
subIdx = pm.ConstantData('subIdx', value=idx_sub, dims='data')
condIdx = pm.ConstantData('condIdx', value=idx_cond, dims='data')
### 事前分布
## μ:指数-正規分布の正規分布側の平均パラメータ
# mu:集団レベル
mu = pm.Uniform('mu', lower=0, upper=100, dims='cond')
# cov matrix
muSigmaSea = pm.Uniform('muSigmaSea', lower=0, upper=100) # 探索
muSigmaMem = pm.Uniform('muSigmaMem', lower=0, upper=100) # 記憶
muRho = pm.Uniform('muRho', lower=-1, upper=1) # 相関係数
muCovMtx = pm.Deterministic('muCovMtx',
pt.stacklists([[pt.pow(muSigmaSea, 2), muSigmaSea*muSigmaMem*muRho],
[muSigmaSea*muSigmaMem*muRho, pt.pow(muSigmaMem, 2)]]))
# muInd:多変量正規分布・個人レベル
muInd = pm.MvNormal('muInd', mu=mu, cov=muCovMtx, dims=('sub', 'cond'))
## σ:指数-正規分布の正規分布側の標準偏差パラメータ
# sigma:集団レベル
sigma = pm.Uniform('sigma', lower=0, upper=100, dims='cond')
# cov matrix
sigmaSigmaSea = pm.Uniform('sigmaSigmaSea', lower=0, upper=100) # 探索
sigmaSigmaMem = pm.Uniform('sigmaSigmaMem', lower=0, upper=100) # 記憶
sigmaRho = pm.Uniform('sigmaRho', lower=-1, upper=1) # 相関係数
sigmaCovMtx = pm.Deterministic('sigmaCovMtx',
pt.stacklists(
[[pt.pow(sigmaSigmaSea, 2), sigmaSigmaSea*sigmaSigmaMem*sigmaRho],
[sigmaSigmaSea*sigmaSigmaMem*sigmaRho, pt.pow(sigmaSigmaMem, 2)]]))
# sigmaInd:多変量正規分布・個人レベル
sigmaInd = pm.MvNormal('sigmaInd', mu=sigma, cov=sigmaCovMtx,
dims=('sub', 'cond'))
### 尤度:切断正規分布
likelihood = pm.TruncatedNormal('likelihood',
mu=muInd[subIdx, condIdx],
sigma=sigmaInd[subIdx, condIdx],
lower=0,
observed=y, dims='data')
### 計算
# 集団レベルのμ、σ、λ、νについて、記憶と探索の差分
muDiff = pm.Deterministic('muDiff', mu[1] - mu[0])
sigmaDiff = pm.Deterministic('sigmaDiff', sigma[1] - sigma[0])【実行結果】なし
2.モデルの外観の確認
### モデルの表示
model【実行結果】

### モデルの可視化
pm.model_to_graphviz(model)【実行結果】

3.事後分布からのサンプリング
乱数生成数は tune を多めにしました。
また、target_accept の値を大きくしました。
NUTSサンプラーに numpyro を利用して、処理時間はおよそ2時間22分でした(こちらも🚅東京・大阪間・・・)
# 事後分布からのサンプリング 2時間22分
with model:
idata = pm.sample(draws=12000, tune=8000, chains=4, target_accept=0.998,
nuts_sampler='numpyro', random_seed=123)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
rhat_idata = az.rhat(idata)
(rhat_idata > 1.1).sum()【実行結果】
「正規分布」モデルと同様に$${\hat{R} \leq 1.1}$$です!収束しています!

4.事後予測
モデルの当てはまり具合を目的変数の事後予測データで確認します。
### 事後予測サンプリング 1分22秒
with model:
idata.extend(pm.sample_posterior_predictive(idata, random_seed=123))【実行結果】

### 事後予測のプロット
fig, ax = plt.subplots(figsize=(10, 4))
pm.plot_ppc(idata, num_pp_samples=100, random_seed=123, ax=ax)
ax.set(xlabel='反応時間(秒)', ylabel='density', title='事後予測プロット');【実行結果】
黒線が観測値の反応時間、オレンジの点線が事後予測値です。
0未満を切断しているので、正規分布モデルよりは妥当性がありそうです。
しかし、反応時間0~2秒あたりの突き抜けた分布を表現することはできませんでした。

(参考:正規分布モデルの事後予測プロット)

5.事後分布サンプリングデータの推定値
一応、パラメータの事後分布の各値を表示してみます。
テキストの表15.1~15.4の正規分布版に相当します。
①集団レベル
### 推論データの要約統計情報の表示 集団レベル
var_names = ['mu', 'sigma']
pm.summary(idata, hdi_prob=0.95, var_names=var_names).round(3)【実行結果】
下の正規分布モデルと対比しながらご覧ください。

(参考:正規分布モデル)

②個人レベル:記憶メインブロック
「coords={'cond': '記憶'}」を指定することで、変数 cond が「記憶」のデータを抽出できます。
### 推論データの要約統計情報の表示 個人レベル 記憶メインブロック
var_names = ['muInd', 'sigmaInd']
(pm.summary(idata, hdi_prob=0.95, var_names=var_names, coords={'cond': '記憶'})
.round(3))【実行結果】
平均 mean が負の値になっています。

(参考:正規分布モデル)

③個人レベル:探索メインブロック
### 推論データの要約統計情報の表示 個人レベル 探索メインブロック
var_names = ['muInd', 'sigmaInd']
(pm.summary(idata, hdi_prob=0.95, var_names=var_names, coords={'cond': '探索'})
.round(3))【実行結果】
こちらも平均値がマイナスです。

(参考:正規分布モデル)

④集団レベルのパラメータの条件差
「記憶-探索」の値です。
### 推論データの要約統計情報の表示 集団レベルの各パラメータの条件差
var_names = ['muDiff', 'sigmaDiff']
pm.summary(idata, hdi_prob=0.95, var_names=var_names).round(3)【実行結果】
平均 mu の95%HDIがマイナスを取っています。

(参考:正規分布モデル)

ちなみにトレースプロットはこんな感じです。
集団レベルのパラメータ推定値の例です。
### トレースプロットの表示 集団レベル
var_names = ['mu', 'sigma']
pm.plot_trace(idata, compact=False, var_names=var_names)
plt.tight_layout();【実行結果】
発散を示すバーコードが多いです(汗)

以上で第15章は終了です。
「指数-正規分布」と仲良くなりたかったです。。。
ちなみにテキストでは「探索目的の違いが指数-正規分布の平均反応時間に与える影響の大部分は(指数分布のパラメータである)$${\lambda}$$の違いによると解釈できるだろう」(括弧は私による補足)と締めくくっています。

おわりに
MCMCの時間
今回のPyMCモデルたちは、MCMCの時間がかなりかかる「強者たち」ばかりでした。
モデルの試行錯誤をする際、MCMCの時間が短いと嬉しいですね!
経験値より、次にあてはまるモデルは比較的MCMC時間が長いと思っています。
観測データが多い
モデルの構造として、階層が深い・次元が多い・多変量
標準サンプラーを利用(パラメータが離散値)
変わった分布を使用
サンプリング数が多い
target_acceptの値が大きい
収束が悪い
今回は変わった分布(指数-正規分布の混合分布)、観測データがそこそこ多い、target_acceptの値が大きいあたりが影響してMCMC時間が長くなったと想像できます。
また、収束が悪いことが時間を要した主因のような気もします。
時間がかかる場合は、お風呂にゆっくりつかったり、2時間ドラマや映画DVDなどを楽しんだりして、ベイズから一旦離れて、リフレッシュしましょう。

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析トピックを PythonとPyMC Ver.5で取り組みます。
豊富なテーマ(お題)を実践することによって、PythonとPyMCの基礎体力づくりにつながる、そう信じています。
日々、Web検索に勤しみ、時系列モデルの理解、Pythonパッケージの把握、R・Stanコードの翻訳に励んでいます!
このシリーズがPython時系列分析の入門者の参考になれば幸いです🍀
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
ベイズ書籍の実践記録も掲載中です。
最後までお読みいただきまして、ありがとうございました。
