
10-2-3 母平均の差の検定と一元配置分散分析 ~ 母平均の差の検定をt-testと1way-ANOVAで挟み撃ち
今回の統計トピック
2つの水準=2標本の母平均の差の検定を$${t}$$検定と一元配置分散分析で実施します。
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
今回の記事の構成
この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」と「知る」を1つの章にまとめます。
続く「実践する」で本問題の一元配置分散分析をEXCEL・R・Pythonで実践いたします。
問題を解きながら知る
📘公式問題集のカテゴリ
線形モデルの分野 ~分散分析の分野
問3 母平均の差の検定と一元配置分散分析(プロ野球チームの年間入場者数)
試験実施年月
統計検定2級 2018年6月 問12(回答番号24,25)
📕公式テキスト
・4.4.1 母平均の差の検定 母分散が未知で等しい場合(152ページ~)
・5.2.1 1元配置分散分析(185ページ~)
問題
公式問題集をご参照ください。
解き方
問題の概要
問題文に記載された「2017年のプロ野球のリーグごとの球団別ホームゲーム年間入場者数」データに基づいて、次の2問を解答します。
問1.2つのリーグの母平均の差の$${t}$$検定に用いる$${t}$$値を計算
問2.2つのリーグを水準とする一元配置分散分析の$${F}$$値を計算
題意
出題の意図には、おそらく次の2つの観点が含まれると思います。
・「対応のない2標本の母平均の差の検定」を「$${t}$$検定」と「一元配置分散分析」の別々の方法で実施できること
・$${t}$$値と$${F}$$値には特別な関係があること
この題意に沿って、解答を検討します。
問1の扱い
実は、問1の$${t}$$検定の問題は、既に解いています!
公式問題集の8章-第6問「母平均の差の検定」に全く同じ問題があります。
詳しい解き方は次のブログをご参照くださいませ。
データ
Pythonを用いてデータを表にまとめます。
### インポート
import pandas as pd
### 入場者数データの登録 data_cen:セ・リーグ、data_pac:パ・リーグ
data_cen = [218, 303, 198, 296, 201, 186]
data_pac = [209, 177, 167, 145, 161, 253]
### 表示データの作成(データフレーム化)
cols = ['球団'] * 6
data_df = pd.DataFrame({'セ': data_cen, 'パ': data_pac}, index=cols).T
data_df['平均'] = data_df.mean(axis=1).round(1)
data_df['偏差平方和'] = \
((data_df.iloc[:, :6].T- data_df['平均'])**2).sum(axis=0).round(0)
display(data_df)【問題に用いるデータ】
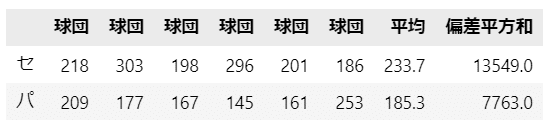
それでは、このデータを用いて、問題を解きましょう。

「題意1:母平均の差の検定の比較」
問1.対応のない2標本の母平均の差の検定に用いる$${\boldsymbol{t}}$$値
①$${t}$$検定
下図の右側に記した「検定統計量$${t}$$」を計算します。
セ・リーグを$${x, m}$$、パ・リーグを$${y, n}$$に当てはめます。

■ プールした分散
まず「プールした分散」を計算しましょう。
【プールした分散の公式】
$${\hat{\sigma}^2 = \cfrac{ \sum^m_{i=1} (x_i-\bar{x})^2 + \sum^n_{j=1}(y_i-\bar{y})^2}{m+n-2}}$$
公式中の各項にデータを当てはめましょう。
・$${\sum^m_{i=1} (x_i-\bar{x})^2}$$→セ・リーグの偏差平方和
・$${\sum^n_{j=1}(y_i-\bar{y})^2}$$→パ・リーグの偏差平方和
・$${m}$$→セ・リーグの球団数
・$${n}$$→パ・リーグの球団数
では計算します。
$$
\begin{align*}
\hat{\sigma}^2 &= \cfrac{ \sum^m_{i=1} (x_i-\bar{x})^2 + \sum^n_{j=1}(y_i-\bar{y})^2}{m+n-2} \\
\\
&=\cfrac{13549+7763}{6+6-2} \\
\\
&=\cfrac{21312}{10} \\
\\
&=2131.2
\end{align*}
$$
プールした分散$${\hat{\sigma}^2}$$は$${2131.2}$$です。
■ 検定統計量$${\boldsymbol{t}}$$
続いて検定統計量$${t}$$を計算します。
【検定統計量$${t}$$の公式】
$${t = \cfrac{\bar{x} - \bar{y}}{\sqrt{ \left(\frac{1}{m}+\frac{1}{n} \right)\hat{\sigma}^2}}}$$
公式中の各項にデータを当てはめましょう。
・$${\bar{x}}$$→セ・リーグの平均値
・$${\bar{y}}$$→パ・リーグの平均値
・$${m}$$→セ・リーグの球団数
・$${n}$$→パ・リーグの球団数
・$${\hat{\sigma}^2}$$→プールされた分散
では計算します。
$$
\begin{align*}
t &= \cfrac{\bar{x} - \bar{y}}{\sqrt{ \left(\frac{1}{m}+\frac{1}{n} \right)\hat{\sigma}^2}} \\
\\
&= \cfrac{233.7-185.3}{\sqrt{ \left(\frac{1}{6}+\frac{1}{6} \right) \times 2131.2}} \\
\\
&= \cfrac{48.4}{\sqrt{\ \frac{1}{3} \times 2131.2}} \\
\\
&= \cfrac{48.4}{\sqrt{710.4}} \\
\\
&=1,8159 \cdots \\
&\fallingdotseq 1.82
\end{align*}
$$
検定統計量$${t}$$の実現値である$${t}$$値は$${1.82}$$です。
問1の解答選択肢は ④ です。
■ 自由度$${\boldsymbol{10}}$$の$${\boldsymbol{t}}$$分布
今回の検定統計量$${t}$$は、自由度$${m+n-2=10}$$の$${t}$$分布に従います。
そこで、自由度$${10}$$の$${t}$$分布と$${t}$$値をグラフにして可視化しましょう。

グラフに有意水準の%点をプロットすると、帰無仮説を棄却できるかどうか分かります。
後ほど、検定をしましょう。

問2 一元配置分散分析に用いる$${\boldsymbol{F}}$$値
計算メカニズムの各項目を埋めていきます。
平方和から取り掛かりましょう。

■ 差の概念:平方和の基礎
平方和は、①データ点の1つずつ「差」を取って2乗して、②全データ点の①の計算結果を足し上げる、という手続きで求められます。
下の図で「差」の分解をしましょう。
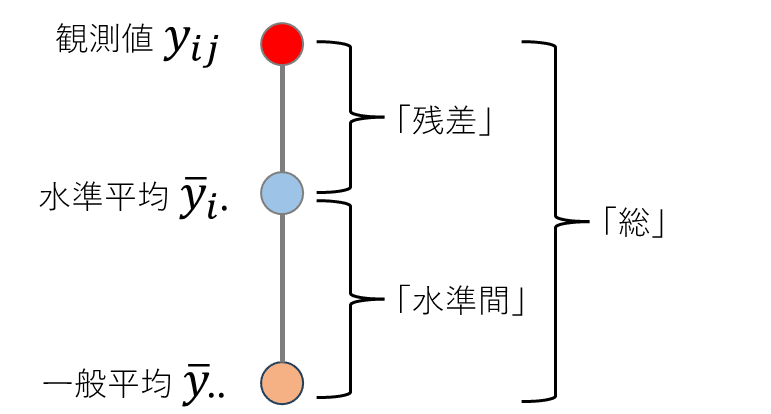
ベースになる「差」は、観測値(赤点)と一般平均=全体の平均(ベージュ点の差であり、「総平方和」に繋がります。
この差を分解します。
まず、水準平均=各水準の平均(青点)の差が「水準間平方和」に繋がります
続いて、観測値(赤点)と水準平均(青点)の差が「残差平方和」に繋がります。
■ 平方和の計算メカニズム表
下図は「平方和」の列の計算表です。
黄色いセルの列が平方和の計算部分です。
「総平方和」、「残差平方和」、「水準間平方和」の役者が揃っています。
№1~12の各データ点ごとに「差」の2乗を計算しています。
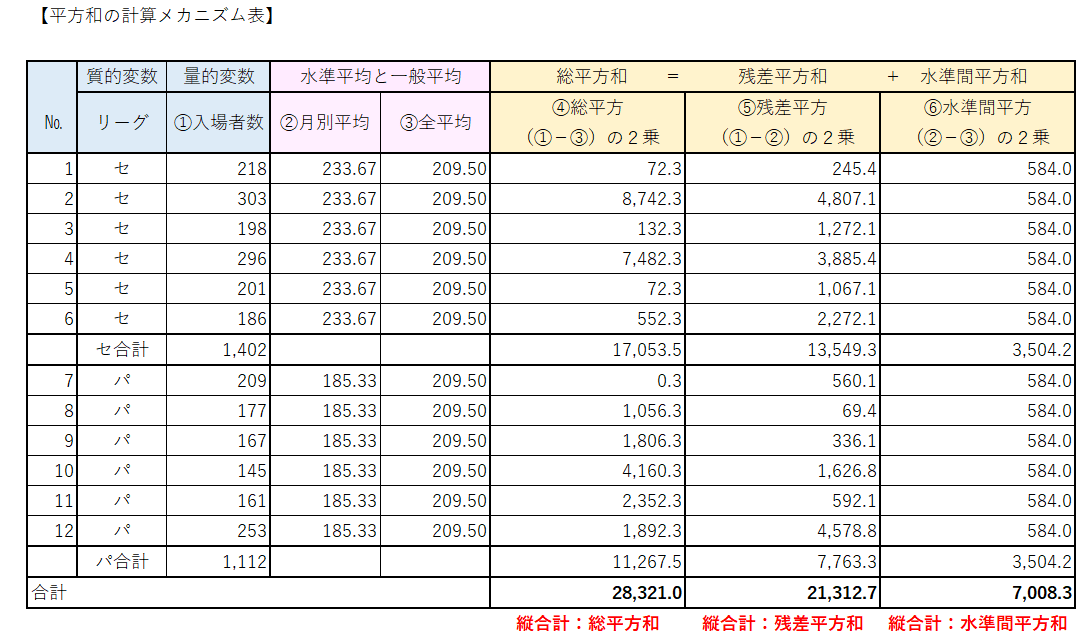
この表の計算を文章・数式にします。
■ 残差平方和
残差平方和は、①水準ごとに「観測値(各データ)-各水準の平均値」を二乗して、②これらの①の計算値を合計して計算できます。
セ・リーグは$${\sum^m_{i=1} (x_i-\bar{x})^2}$$、パ・リーグは$${\sum^n_{j=1}(y_i-\bar{y})^2}$$です。
この数式は、プールした分散の計算で用いた「偏差平方和」です。
つまり、残差平方和は、各水準の偏差平方和を足したものなのです。
そして、偏差平方和の値は問題文で次表の右列のように与えられています。

セ:$${13549}$$、パ:$${7763}$$を用いて、さっそく計算しましょう。
$$
\begin{align*}
&\sum^m_{i=1} (x_i-\bar{x})^2 + \sum^n_{j=1}(y_i-\bar{y})^2 \\
&= 13549+7763 \\
&=21312
\end{align*}
$$
残差平方和は$${21312}$$です。
なお、「計算メカニズム表」の残差平方和の値を使って、小数点端数を四捨五入すると「$${21313}$$」になります。
この記事では、残差平方和は$${\boldsymbol{21313}}$$、とします。
■ 水準間平方和
水準間平方和は、①水準ごとに「各水準の平均値-全体の平均値」を2乗して、②これらの①の計算値を合計して計算できます。
全体の平均値を計算します。
セ・パの球団数が同じなので、セ・パの平均値を足して2で割って求めましょう。
$${(233.7+185.3)/2=209.5}$$
全体の平均値は$${209.5}$$です。
次にセ・リーグの平方和を計算します。
セ・リーグの球団数は6です。
「セ・リーグの平均値-全体の平均値」の2乗を6球団分計算します。
なお、問題文で与えられたセ・リーグの平均値を用いると計算誤差が大きくなるので、平均値はセ・リーグ合計を球団数で割って求めます。
$${((1402/6)-209.5)^2 \times 6 = 3504.17}$$
続いてパ・リーグの平方和を計算します。
パ・リーグの球団数は6です。
「パ・リーグの平均値-全体の平均値」の2乗を6球団分計算します。
平均値はパ・リーグ合計を球団数で割って求めます。
$${((1112/6)-209.5)^2 \times 6 = 3504.17}$$
両リーグの平方和を足して水準間平方和の完成です。
$${3504.17+3504.17=7008.34}$$
水準間平方和は$${\boldsymbol{7008}}$$です。
(注)問題集の解答$${7009}$$と相違するのは、小数点以下の丸め処理が異なるためです。
■ 総平方和
「総平方和=水準間平方和+残差平方和」です。
$${7008+21313=28321}$$
総平方和は$${\boldsymbol{28321}}$$です。
ここまでの計算結果を一元配置分散分析表に記入しましょう。

■ 自由度
自由度の求め方を確認しましょう。

水準間(リーグ間)の自由度は、水準(リーグ)の数$${a=2}$$から$${1}$$を差し引いた$${1}$$です。
残差の自由度は、標本サイズ(全球団数)$${n=12}$$から$${a=2}$$を差し引いた$${10}$$です。
一元配置分散分析表に記入しましょう。

■ 平均平方(分散)
一元配置分散分析表の横に走る青い割り算の記号に沿って、「平方和÷自由度=平均平方」の計算をしましょう。
・水準間(リーグ間):$${7008/1=7008}$$
・残差:$${21313/10 =2131.3}$$
一元配置分散分析表に記入しましょう。

■ $${\boldsymbol{F}}$$値
一元配置分散分析表の縦に走る青い割り算の記号に沿って、「水準間平均平方÷残差平均平方=$${F}$$値」の計算をしましょう。
$${7008/2131.3=3.288 \cdots \fallingdotseq 3.288}$$
一元配置分散分析表が完成しました!

(注)小数点以下の丸め処理が異なるため、問題集の解答と値が相違します。
$${F}$$値は$${3.288}$$です。
解答選択肢の中で近似するのは$${3.30}$$です。
問2の解答選択肢は ④ です。
■ 自由度$${\boldsymbol{(1, 10)}}$$の$${\boldsymbol{F}}$$分布
今回の$${F}$$値は、自由度$${(1, 10)}$$の$${F}$$分布に従います。
そこで、自由度$${(1, 10)}$$の$${F}$$分布と$${F}$$値をグラフにして可視化しましょう。

グラフのタイトルに$${p}$$値を表示しました。
一元配置分散分析表に$${p}$$値を記入して最終化しましょう。

以上で一元配置分散分析表を用いた$${F}$$値の計算を終わります。
■ 母平均の差の検定
最後に、母平均の差の検定の結論を考えましょう。
有意水準を$${5\%}$$とし、$${t}$$検定は両側検定、一元配置分散分析は片側・上側検定にします。
📈対応のない2標本の母平均の差の$${\boldsymbol{t}}$$検定
$${t}$$分布のパーセント点表から、自由度$${10}$$の上側確率$${2.5\%}$$点を取得しましょう。

上側$${2.5\%}$$点は$${2.228}$$です。
$${t}$$値$${1.82}$$でした。
$${t}$$値は上側$${2.5\%}$$点より小さいので、帰無仮説を棄却できません。
まとめます。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却されず、両リーグの入場者数の母平均に差があるとは言えないです。
自由度$${10}$$の$${t}$$分布のグラフに、$${t}$$値と両側の$${2.5\%}$$点を描画して、$${t}$$値が棄却域から外れていることを確かめましょう。

📈一元配置分散分析による水準間の母平均の差の検定
$${F}$$分布のパーセント点表から、自由度$${(1,10)}$$の上側確率$${5%}$$点を取得しましょう。

上側$${5\%}$$点は$${4.965}$$です。
$${F}$$値$${3.288}$$でした。
$${F}$$値は上側$${5\%}$$点より小さいので、帰無仮説を棄却できません。
まとめます。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却されず、両リーグの入場者数の母平均に差があるとは言えないです。
自由度$${(1,10)}$$の$${F}$$分布のグラフに、$${F}$$値と上側$${5\%}$$点を描画して、$${F}$$値が棄却域から外れていることを確かめましょう。

📈 $${p}$$値の補足
小数点以下の数値を含めて計算すると、$${t}$$値の$${p}$$値と、$${F}$$値の$${p}$$値は一致します。
Python の scipy.stats で$${t}$$検定(両側検定)と一元配置分散分析を実施して、$${p}$$値を比較してみましょう。
from scipy inport stats
### 対応のない2標本のt検定(両側検定)と一元配置分散分析
print(stats.ttest_ind(data_df.iloc[0, :6], data_df.iloc[1, :6],
alternative='two-sided'))
print(' ', stats.f_oneway(data_df.iloc[0, :6], data_df.iloc[1, :6]))【出力結果】

上の行は、$${t}$$値(statistic)とその$${p}$$値(pvalue)。
下の行は、$${F}$$値(statistic)とその$${p}$$値(pvalue)。
$${p}$$値が一致していることが分かります。

「題意2:$${\boldsymbol{t}}$$と$${\boldsymbol{F}}$$値の特別な関係」
ある条件を満たす$${t}$$値と$${F}$$値には特別な関係が生まれます。
【重要な性質】$${t}$$分布と$${F}$$分布の関係
自由度$${m}$$の$${t}$$分布に従う確率変数$${t}$$の2乗$${t^2}$$は、自由度$${(1, m)}$$の$${F}$$分布に従います。
【参考記事】
こちらの記事で「$${t}$$分布と$${F}$$分布の関係」にふれています。
本問題では、$${t}$$値(正確には検定統計量$${t}$$)は自由度$${10}$$の$${t}$$分布に従います。
つまり、上述の確率変数$${t}$$の条件を満たしています。
そして、本問題で解く$${F}$$値(正確には検定統計量$${F}$$)は、自由度$${(1,10)}$$の$${F}$$分布に従うのです!
これって偶然!?重要な性質の文章を整理しましょう。
「自由度$${10}$$の$${t}$$分布に従う$${t}$$値の2乗$${t^2=1.82^2}$$は、自由度$${(1, 10)}$$の$${F}$$分布に従います。」
$${t}$$値の2乗である$${1.82^2\fallingdotseq3.3}$$が$${F}$$値です。
問2の解答選択肢は ④ 3.30 です。
【ヒント💡】
$${t}$$値と$${F}$$値を求めるとき、$${F}$$値の従う$${F}$$分布の第1自由度が$${1}$$で、かつ、第2自由度が$${t}$$値の従う$${t}$$分布の自由度と同じ$${m}$$の場合、「$${t}$$値の2乗=$${F}$$値」、「$${F}$$値の平方根=$${t}$$値」となることを活用しましょう。
長い道のり、お疲れ様でした。
解答
〔1〕④、〔2〕④ です。
難易度 ふつう
・知識:対応のない母平均の差の$${t}$$検定、一元配置分散分析、$${t}$$値と$${F}$$値の関係
・計算力:数式組み立て(低)、電卓(中)
・時間目安:3問合計 5分
実践する
一元配置分散分析を実践する
問題集のデータを用いて、一元配置分散分析を EXCEL、R、Python で実践しましょう!
EXCELで作成してみよう!
データ分析機能の「分散分析-一元配置」を利用して、サクッと一元配置分散分析を実施しましょう。
一元配置分散分析表の作成
メニューより、「データ」>「データ分析」を指定して、「データ分析」画面を開き、「分散分析:一元配置」を指定して「OK」ボタンをクリックします。
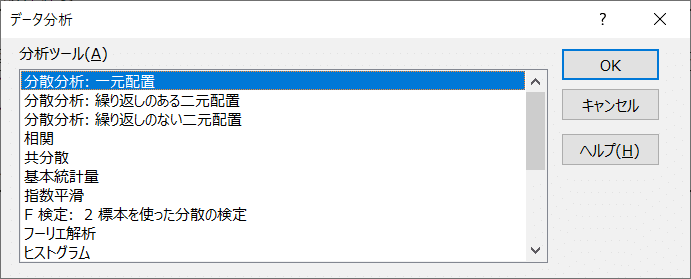
「分散分析:一元配置」画面の入力範囲に項目名を含めたデータの範囲を指定します。
データ方向は「列」です。
「OK」ボタンをクリックすると、分散分析表が表示されます。

一元配置分散分析表の確認
EXCEL画面に一元配置分散分析表が表示されました。
上段に「リーグ」別の基本統計量、下段に分散分析表です。

下段に注目しましょう。

グループ間(水準間)は、「リーグ」間の平方和(変動)、平均平方(分散)です。
グループ内(水準内)は、残差平方和(変動)、平均平方(分散)です。
$${F}$$値(観測された分散比)は$${3.288}$$、$${p}$$値は$${0.100}$$。
統計的仮説検定
有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値は有意水準より大きいので、帰無仮説を棄却できません。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却されず、両リーグの入場者数の母平均に差があるとは言えないです。
まとめ
かなりシンプルな操作で本格的な分散分析表を作成できました。
(手作業と比べてみてください!)
ぜひぜひ、いろんなグループのデータ平均を比べてみましょう!
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

R で作成してみよう!
R スクリプトで一元配置分散分析を実践します。
コードはめっちゃシンプルです。
① データの設定
リーグと入場者数を R スクリプトに直接、入力します。
### データの設定
リーグ <- rep(c('セ', 'パ'), times=c(6, 6))
入場者数 <- c(218, 303, 198, 296, 201, 186, 209, 177, 167, 145, 161, 253)
data <- data.frame(リーグ, 入場者数)
# データの要約表示
str(data)
summary(data)【出力結果】
データは質的変数「リーグ」と量的変数「入場者数」で構成されます。

② リーグ別の基本統計量の表示
psych ライブラリの describeBy 関数を利用します。
### リーグ別の統計量
library(psych)
describeBy(data$入場者数, data$リーグ)【出力結果】
セ・パ両リーグの基本統計量が表示されました。
データの数(n)、平均(mean)、標準平均(sd)、中央値(median)、最小値(min)、最大値(max)などを確認できます。
平均値の差は、$${233.67-185.33=48.34}$$(万人)です。

③ 箱ひげ図の描画
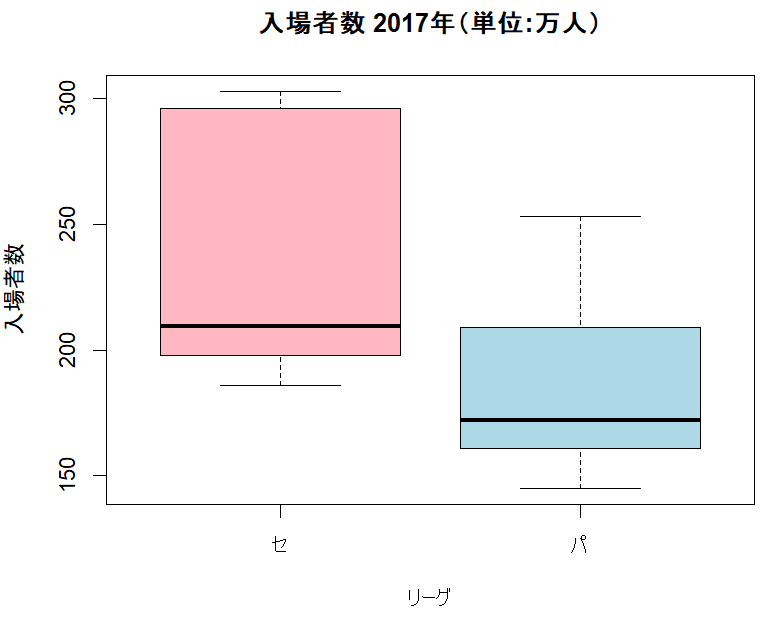
箱ひげ図でリーグごとのデータの外観を確認しましょう。
### 箱ひげ図グラフ
boxplot(入場者数 ~ リーグ, data=data,
main='入場者数 2017年(単位:万人)',
col=c('lightpink', 'lightblue'))【出力結果】
セ・リーグの球団のほうが入場者数が多い印象です。
中央値(箱の中の太横線)は近い感じがします。
④ 分散分析の実行
真打ちの登場です。
たった1行で分散分析ができます!
### 分散分析の実施と結果表示
anova(aov(入場者数 ~ リーグ, data=data))【処理結果】

$${p}$$値(Pr(>F))の表示があるので、検定の結論を出しやすいです。
有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値$${0.09985}$$は有意水準より大きいので、帰無仮説を棄却できません。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却されず、両リーグの入場者数の母平均に差があるとは言えないです。
まとめ
R のコードは非常にシンプルです。
シンプル・イズ・ベストな方にお勧めいたします。
Rサンプルファイルのダウンロード
こちらのリンクからRスクリプト形式のサンプルファイルをダウンロードできます。

Pythonで作成してみよう!
3つのライブラリで一元配置分散分析を実施します。
① インポート
### インポート
# 数値計算
import numpy as np
import pandas as pd
# 統計処理
from scipy import stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
import pingouin as pg
# 可視化
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'② データの設定
リーグと入場者数をコードに直接、入力します。
### データの設定
# 質的変数と目的変数の項目名の設定
cat_col = 'リーグ'
target_col = '入場者数'
# データの設定
league = ['セ'] * 6 + ['パ'] * 6
visit = [218, 303, 198, 296, 201, 186, 209, 177, 167, 145, 161, 253]
# データフレーム化
data = pd.DataFrame({cat_col: league, target_col: visit})
# データの表示
print('data.shape', data.shape)
display(data)【出力結果】

③ リーグ別の要約統計量の表示
pandas の ピボットテーブル関数を用いて、リーグ別の要約統計量をデータフレーム形式で作成します。
aggfunc 引数で統計量を指定します。
### カテゴリ別の要約統計量
data.pivot_table(index=None, columns=cat_col, values=target_col,
aggfunc={target_col: [len, np.sum, np.mean, np.std, min,
np.median, max]},
sort=False).round(3)【出力結果】

リーグが横に並んでいます。「mean」が平均です。
セ・リーグの方が平均値が高いですが、平均値の差、約48(万人)は果たして差がある、と言えるのでしょうか・・・
④ 箱ひげ図の描画
各リーグの入場者数のばらつきを箱ひげ図で確認しましょう。
seaborn の boxplot を利用します。
### 箱ひげ図の描画
sns.boxplot(x=cat_col, y=target_col, data=data);【出力結果】

箱ひげ図をみた限りでは、セ・リーグの球団の入場者数は多いような感じがします。
⑤ 分散分析の実行
statsmodels、scipy.stats、pingouin の分散分析をコードを比べてみましょう(結果は同一です)。
■ statsmodels
回帰分析と同じように、ols(最小二乗法)に fit させてから、「anova_lm」で分散分析を実行します。
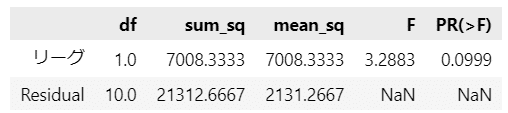
### 分散分析 statsmodels
# df:自由度、sum_sq:平方和、mean_sq:平均平方、F:F値、PR(>F):上側片側確率のp値
# モデルの定義・フィット
anova = smf.ols('入場者数 ~ リーグ', data=data).fit()
# 分散分析の実行
result_sm = sm.stats.anova_lm(anova, typ=1)
result_sm.round(4)【出力結果】
【統計的仮説検定の結論】
$${p}$$値(Pr(>F))の表示があるので、検定の結論を出しやすいです。
有意水準を$${5\%}$$とする場合の統計的仮説検定を実施してみましょう。
$${p}$$値$${0.0999}$$は有意水準より大きいので、帰無仮説を棄却できません。
【結論】
有意水準$${\boldsymbol{5\%}}$$で帰無仮説は棄却されず、両リーグの入場者数の母平均に差があるとは言えないです。
■ scipy.stats
一元配置分散分析用の関数 f_oneway を利用します。
この関数は、引数に「水準別」(リーグ別)に分けられたデータを指定する必要があります。
そこで、コードの前段で、水準別データを作成しています。
pandas の groupby を使って、リーグ別にデータを格納する「data_by_category」を作成しています。
### 分散分析 scipy.stats
# GroupByオブジェクトの生成
groups = data.groupby(cat_col, sort=False)
# 水準別データの作成
data_by_category = []
for category in list(groups.groups):
data_by_category.append(groups.get_group(category)[target_col])
# 分析分析の実行&データフレームに格納
result_stats = pd.DataFrame(columns=['F値', 'p値'])
result_stats.loc[cat_col] = stats.f_oneway(*data_by_category)
result_stats.round(4)【出力結果】

f_oneway 関数の出力は$${F}$$値と$${p}$$値の2項目です。
取り急ぎ「3つ以上のグループの母平均の差の検定をしたい」という場合に利用する感じでしょう。
■ pingouin
anova 関数の1行を書くことで分散分析を行います。
一番シンプルなコードだと思います。
引数は、dv:目的変数(従属変数)、between:水準を含む変数(水準間)などです。
### 分散分析 pingouin
## Source:要因、SS:平方和、DF:自由度、MS:平均平方、F:F値、P-unc:p値、np2:相関比
result_pg = pg.anova(dv=target_col, between=cat_col, data=data, detailed=True)
result_pg.round(4)【出力結果】

一元配置分散分析の「水準間」「残差」(水準内:Within)行が表示されました。
分散分析表の項目が網羅されています。
そして、相関比$${\eta^2}$$(np2)の表示もあります。
相関比は、質的変数と量的変数の相関関係にかかわる統計量です。
「水準間平方和÷総平方和」で計算できます。
⑥ 各水準の信頼区間の描画
各リーグの母平均の信頼区間をグラフに描画します。
思いの外、長いコードになりました。
■ 計算要素の算出
### 信頼区間の計算要素の算出
# 設定 信頼係数
cf = 0.95
# 計算要素の算出
df = result_sm.df.Residual # 残差の自由度
mean_square = result_sm.mean_sq.Residual # 残差の平均平方
t_ppf = stats.t.ppf((1 + cf) / 2, df) # t分布の上側cf/2%点
counts = groups[[target_col]].count() # 各水準のデータ数
means = groups[[target_col]].mean() # 各水準の平均値
# 信頼区間の片幅(正値側)の算出
ci_upper = t_ppf * np.sqrt(mean_square / counts)
# 計算要素の表示
print(f't分布の上側{(1-cf)/2:.1%}: {t_ppf:.3f}, 残差の平均平方: {mean_square:.3f}, '
f'信頼区間の片幅(正値側): {ci_upper.iloc[0, 0]:.3f}')【出力結果】

■ 信頼区間の表示
pandas のデータフレーム形式に加工するので、コードが増えました。
### 水準別の信頼区間の表示
# 下端の設定
groups_ci = (means - ci_upper).rename(columns={target_col: '下端'})
# 平均の設定
groups_ci['平均'] = means
# 上端の設定
groups_ci['上端'] = means + ci_upper
# 表示
pd.options.display.float_format = None
groups_ci.T.round(2)【出力結果】

■ グラフ描画
matplotlib の errorbar 関数を利用します。
信頼区間の片側の値を引数「yerr」に渡します。
### エラーバー付きプロットの描画
# エラーバー付きプロットの描画
plt.errorbar(means.index, means[target_col], yerr=ci_upper[target_col],
marker='o', markersize=15, linewidth=0, elinewidth=1,
ecolor='gray', capsize=10)
# 修飾
plt.xlim(-1, 2)
plt.title('入場者数 母平均の95%信頼区間')
plt.xlabel('リーグ')
plt.ylabel('入場者数(万人)')
plt.show()【出力結果】

母平均の平均の95%信頼区間は、ヒゲの上下の範囲です。
ヒゲの長さは、片側 41.994 (単位:万人)です。
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
以上で本記事の一元配置分散分析を完了いたします。
長旅、お疲れ様でした。
最後までお付き合いしてくださり、ありがとうございました。
おわりに
プロ野球の各リーグの年度別入場者数は、「一般社団法人日本野球機構」様の「統計データ」のページで公開されています。
【統計データのリンク】
年間入場者数の上のピークは両リーグとも 2019年 でした。
新型ウィルスの厳重な規制が解除された今年の入場者数は、過去最高を更新するでしょうか!
楽しみですね🌺
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
