「Pythonではじめる異常検知入門」を寄り道写経～第２章「異常検知のデータサイエンス」

2024年3月20日 09:53

第２章「異常検知のデータサイエンス」

書籍の著者　笛田薫先生、江崎剛史先生、李鍾賛先生

この記事は、テキスト「Pythonではじめる異常検知入門」の第２章「異常検知のデータサイエンス」の通称「寄り道写経」を取り扱います。

今回はデータの可視化と回帰モデルの変数選択に寄り道しました。
ではテキストを開いて異常検知の旅に出発です🚀

はじめに

テキスト「Pythonではじめる異常検知入門」のご紹介

このシリーズは書籍「Pythonではじめる異常検知入門」（科学情報出版、「テキスト」と呼びます）の異常検知の理論・数式とPythonプログラムを参考にしながら、テキストにはプログラムの紹介が無いけれども気になったテーマ、または、テキストのプログラム以外の方法を試したいテーマを「実験的」にPythonコード化する寄り道写経ドキュメンタリーです。

テキストは、2023年4月に発売された異常検知の入門書です。
数式展開あり、Python実装ありのテキストなのです。
Jupyter Notebook 形式のソースコードと csv 形式のデータは、書籍購入者限定特典として書籍掲載のURLからダウンロードできます。

■ テキストの概要
テキストは以下の３部で構成されていて、段階的に異常検知に近づいて行きます。

１．異常検知の実装に必要と考えられる知識習得の章
　（第２章、第３章、第４章）
２．入力変数と出力変数があるデータの異常検知の章
　（第５章、第７章）
３．時系列データの異常検知の章
　（第６章、第７章）

Python実装を用いて論点を深く掘り下げる異常検知のテーマは３つです。
主に第５～７章です。

・ホテリングの$${T^2}$$法
・One-Class SVM
・時系列データ（残差が平均０の正規分布に従う場合の異常度）

また、付録的な扱いでアイソレーションフォレストの実装も行います。

■ 通読後の所感
個人的な感想になりますが、テキスト第５章以降はPythonによる異常検知の具体的な実践を行えて、とても楽しかったです！
ホテリングの$${T^2}$$法、One-Class SVM、時系列データの異常検知のスキルアップができました。
一方で第１章から第４章までは、異常検知色が濃いのか薄いのか、よく分かりませんでした。
また計算例等に Python コードが用意されてないケースもあり、コードで数式・モデルにお近づきしたい派の私はモヤモヤすることがありました。

そこで寄り道写経に傾斜しました！

■ 寄り道写経って？
寄り道写経は、テキストの実践を通じて「プログラムは紹介されていないけど、この数式をPythonで実装したらどうなる？」とか「テキストと異なるライブラリ等を用いて動かしたらどうだろう？」などと感じたことを、個人の興味でテーマにすくいあげて、Pythonのサンプルコードを書く活動です。

趣味をブログ化しただけです。スミマセン。

■ 大切にしたいこと
寄り道写経は最後までテキストを楽しむ工夫の一つです。
もう１つ大切な工夫があります。
それは「おおらかな気持ちで」読み進めることです。
テキストからアレコレ検知してしまったときには、呪文「ま、いっか」を唱えて深呼吸しましょう。
それワカチコワカチコ♬

ではテキストを開いて異常検知の旅に出発です🚀

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonではじめる異常検知入門－基礎から実践まで－」初版、著者笛田薫／江崎剛史／李鍾賛、オーム社

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

第２章異常検知のデータサイエンス

Jupyter Notebook 形式（拡張子 .ipynb）でPythonコードを書きます。

テキストのこの章は主に「可視化」「回帰分析」「主成分分析」「ベイズの定理」を掲載しています。

この記事は以下の３点の寄り道写経に取り組みます。

① 可視化をseaborn化（2.1節関連）
　見た目重視の可視化を目指します！
② 回帰分析をscipyと行列で実施（2.2節関連）
　何となくscikit-learn以外の実装に寄り道したくなりました。
③ Stepwise法による変数選択（2.2節関連）
　テキストには変数選択の結果のみ掲載されています。
　コード実装するとどうなるか気になって、寄り道しました。

インポート

### インポート

# 数値・確率計算
import pandas as pd
import numpy as np
import scipy.stats as stats

# 確率モデル
import statsmodels.api as sm

# 機械学習
from sklearn.linear_model import LinearRegression

# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'

Google Colab をご利用の場合は「描画」箇所を以下のように差し替えてください。

!pip install japanize_matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
import seaborn as sns

2.1 得られたデータの見える化（可視化）

テキストが利用する「Davisの身長と体重のデータ」をwebサイトから直接読み込み、テキストの可視化を seabornで実装します。

データの読み込み
次のURLの Item 「Davis」から「Davis.csv」を直接読み込みます。
異常検知界隈では有名なデータセットだそうです。

【引用元サイト】

### データの読み込み
URL = 'https://vincentarelbundock.github.io/Rdatasets/csv/carData/Davis.csv'
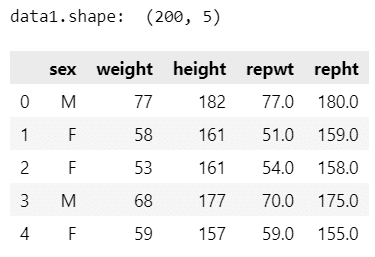
data1 = pd.read_csv(URL, usecols=[1, 2, 3, 4, 5])
print('data1.shape: ', data1.shape)
display(data1.head())

【実行結果】
200人の体重[kg]・身長[cm]のデータです。
変数は、性別・実測体重・実測身長・報告体重・報告身長です。

ヒストグラム
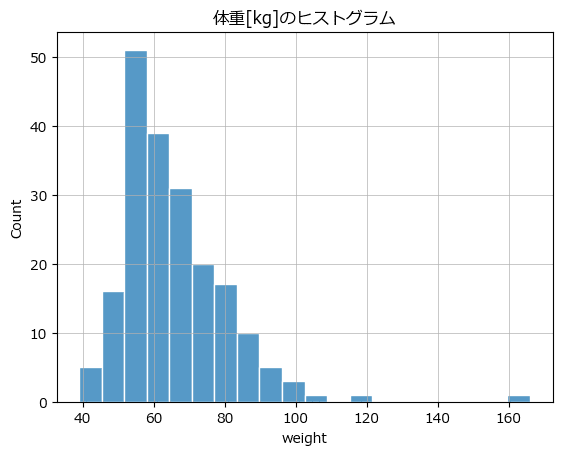
テキスト図2-1に相当する変数 weight のヒストグラムを seaborn を用いて描画します。

### 図2-1 １つの変量のバラツキを確認するヒストグラム
sns.histplot(data=data1, x='weight', ec='white')
plt.title('体重[kg]のヒストグラム')
plt.grid(lw=0.5);

【実行結果】
weight : 実測体重の 160 付近に異常値のようなデータがあります！

棒グラフ
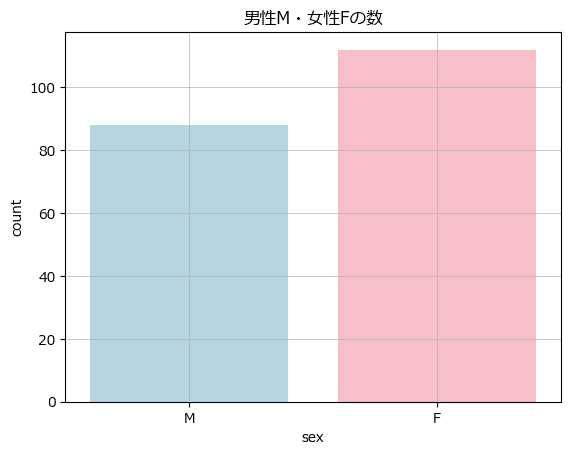
テキスト図2-2に相当する変数 sex：性別ごとの個数を棒グラフを seaborn で描画します。

### 図2-2 各項目におけるデータの数を比較する棒グラフ
sns.countplot(data=data1, x='sex', hue='sex', palette=['lightblue', 'lightpink'])
plt.title('男性M・女性Fの数')
plt.grid(lw=0.5);

【実行結果】
データ200件中、男性が90件弱、女性が110件強です。
やや女性のデータが多い印象でしょうか。

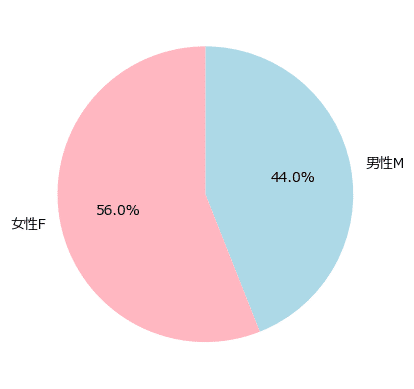
円グラフ
この棒グラフを円グラフで表現してみましょう。
seaborn の円グラフ描画が分からなかったので、matplotlib を用いました。

### 円チャート
plt.pie(data1['sex'].value_counts().sort_index(ascending=False),
        counterclock=False, startangle=90, labels=['男性M', '女性F'],
        colors=['lightblue', 'lightpink'], autopct='%1.1f%%');

【実行結果】
男女比が分かりました。

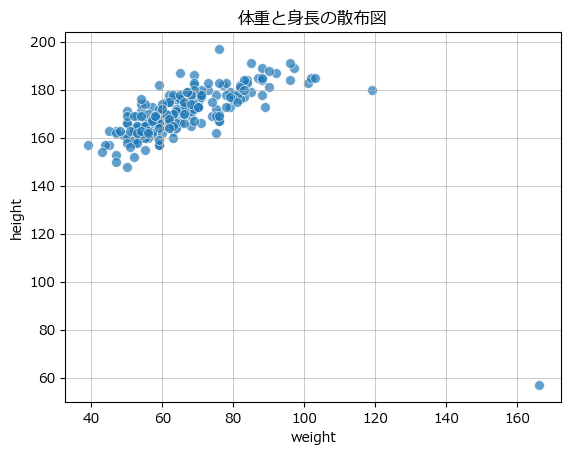
散布図
テキスト図2-3に相当する変数 weight と height の散布図を seaborn で描画します。

### 図2-3 ２つの連続する変量の関係性を可視化する散布図
sns.scatterplot(data=data1, x='weight', y='height', s=50, alpha=0.7)
plt.title('体重と身長の散布図')
plt.grid(lw=0.5);

【実行結果】
横軸 160 付近のデータ点は他のデータ群から大きく外れています。
異常検知っぽくなってきましたね！
横軸 120、縦軸 180 あたりの点も外れ値なのでしょうか？？？

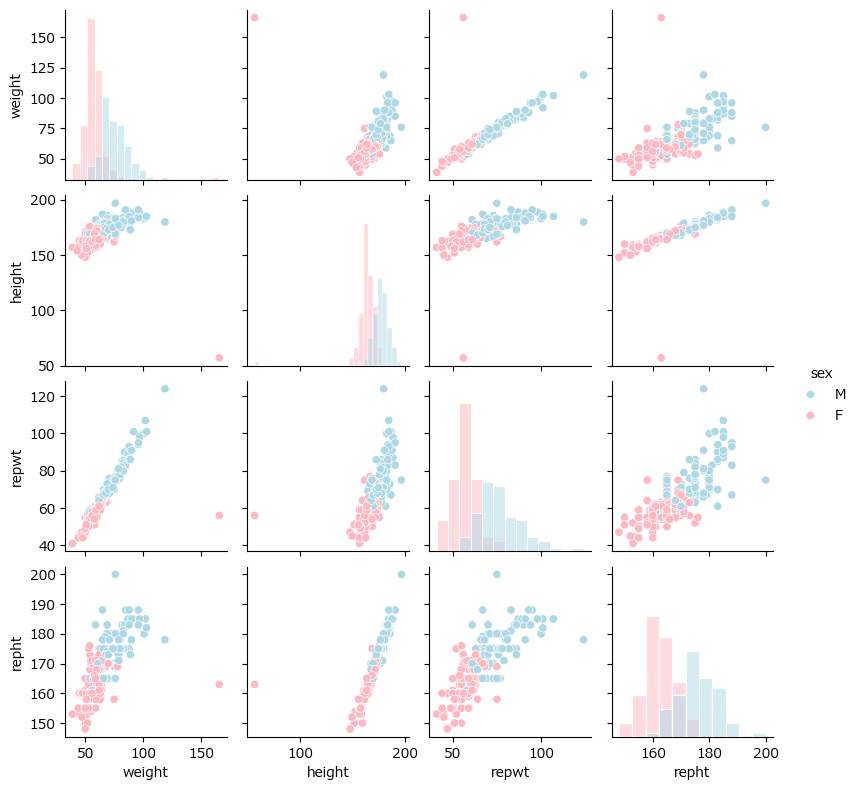
散布図行列
テキスト図2-4に相当する散布図をテキストと同じ seaborn で描画します。
性別を hue に設定して、性別ごとの分布が分かるように改造しました

### 図2-4 複数の連続する変量の関係性を可視化する散布図行列
sns.pairplot(data=data1, hue='sex', diag_kind='hist', height=2, 
             palette=['lightblue', 'lightpink'], diag_kws={'ec': 'white'});

【実行結果】
あの外れ値は女性のデータのようです。

可視化ゾーンはここまでです。

2-2 得られたデータの数式化：回帰モデル

テキストが利用する「アメリカ50州における犯罪率データ」をwebサイトから直接読み込み、scikit-learn以外の方法による回帰係数の算出と、Stepwise法（変数減少法）の実装に取り組みます。

データの読み込み
次のURLの crime data から「crime.txt」を直接読み込みます。

【引用元サイト】

### データの読み込み
URL = r'https://hastie.su.domains/StatLearnSparsity_files/DATA/crime.txt'
data2 = pd.read_csv(URL, sep='\t',
                    usecols=[0, 2, 3, 4, 5, 6],
                    names=['Y', 'X1', 'X2', 'X3', 'X4', 'X5'])
print('data2.shape: ', data2.shape)
display(data2.head())

【実行結果】
50州のデータです。

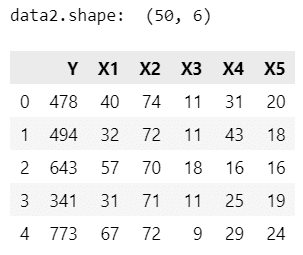
変数はざっくり、以下のとおりです。
Y: 犯罪率
X1: 警察官の年間予算
X2: 高校卒業人口割合（25歳以上）
X3: 高校に通っていない人口割合（16～19歳）
X4: 大学生の人口割合（18～24歳）
X5: ４年制大学卒業人口割合（25歳以上）

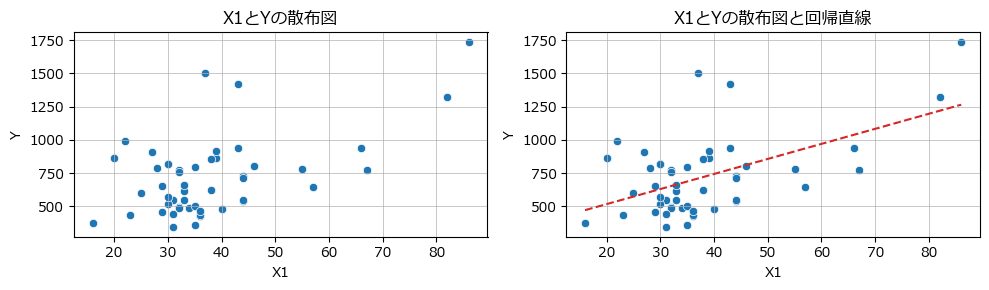
単回帰と回帰直線付き散布図
説明変数 X1 と目的変数 Y の散布図を描画します。
scipy で回帰係数を算出して、seaborn で描画します。

### 図2-5 ２変数のデータの散布図（左図）と単回帰モデルを追加した図（右図）

## 回帰分析 by scipy.stats
# 傾きと切片の算出
slope, intercept = stats.linregress(x=data2['X1'], y=data2['Y'])[0:2]
print(f'切片: {intercept:.4f}, 傾き: {slope:.4f}')
# x軸の値の設定
xval = np.linspace(data2['X1'].min(), data2['X1'].max(), 1001)
# 回帰直線のy軸の値の算出
lmval = intercept + slope * xval

## 描画処理
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10, 3))
# 左の散布図の描画
sns.scatterplot(data=data2, x='X1', y='Y', ax=ax1)
ax1.set(title='X1とYの散布図')
ax1.grid(lw=0.5)
# 右の散布図＋回帰直線の描画
sns.scatterplot(data=data2, x='X1', y='Y', ax=ax2)
ax2.plot(xval, lmval, color='tab:red', ls='--')
ax2.set(title='X1とYの散布図と回帰直線')
ax2.grid(lw=0.5)
plt.tight_layout();

【実行結果】

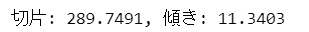
重回帰
テキスト18～19ページの重回帰式$${\boldsymbol{y} = \boldsymbol{X} \boldsymbol{\beta} + \boldsymbol{\varepsilon}}$$の回帰係数を算出します。
以下の行列計算を用いて回帰係数を算出してみます。

$$
\boldsymbol{\beta} = (\boldsymbol{X}^{\top} \boldsymbol{X})^{-1} \boldsymbol{X}^{\top} \boldsymbol{y}
$$

### 重回帰 行列で計算

## 指数表示を回避
np.set_printoptions(precision=6,suppress=True)

## データセットの作成
# 定数項のためのデータ作成
const = np.ones(len(data2)).reshape(-1, 1)
# 説明変数の作成（定数項を追加）
X = np.concatenate([const, data2.drop(columns=['Y']).values], axis=1)
# 目的変数の作成
y = data2['Y'].values

## 回帰係数の算出と表示
beta = np.linalg.inv(X.T @ X) @ X.T @ y
print(f'y = {beta[0]:.4f} {beta[1]:+.4f}x1 {beta[2]:+.4f}x2',
      f'{beta[3]:+.4f}x3 {beta[4]:+.4f}x4 {beta[5]:+.4f}x5')

【実行結果】
回帰式の形式で出力してみました。テキストの結果と比べていかがでしょう？

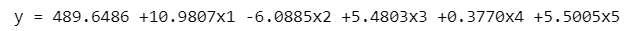
Stepwise法による変数選択
「アメリカ50州における犯罪率データ」を引き続き利用して、テキスト21～22ページに記載の「AICで評価するStepwise法（変数減少法）」を statsmodels で実装します。

まず回帰分析実行関数を定義します。
statsmodels の最小二乗法 OLS を利用します。
statsmodels は AIC を計算してくれるのです。

### 回帰分析実行関数の定義

def exec_linear_regression_sm(X, y):
    # 回帰モデルのインスタンス生成・学習・予測
    X_const = sm.add_constant(X)
    lm_model = sm.OLS(endog=y, exog=X_const)
    lm_result = lm_model.fit()
    # 変数名の取得
    vars = ['const'] + X.columns.values.tolist()
    # AICの取得
    aic = lm_result.aic
    # 学習結果から切片と傾きの取得
    coef = lm_result.params.values.tolist()
    # 戻り値：coefのindex0は切片,index1以降が傾き
    return {'vars': vars, 'aic': aic, 'coef': coef}

ではStepwise法の実行です。
コードは長～いです。

### Stepwise法による変数選択の実行

## データセットの作成
# 説明変数の作成
X = data2.drop(columns=['Y'])
# 目的変数の作成
y = data2['Y'].values
# 選択変数の設定
stepwise_vars = X.columns

## 全ての説明変数による重回帰の実行
print(f'--- 説明変数の数: {len(stepwise_vars)} ---')
result = exec_linear_regression_sm(X, y)
print(result)
best_aic = result['aic']
best_vars = result['vars']
best_coefs = result['coef']

## Stepwise: 選択変数が１つになるまで変数を１つづつ減らして回帰分析を繰り返し実行
while len(stepwise_vars) > 1:
    # 除外変数を格納する変数の準備
    drop_col = None
    print(f'\n--- 説明変数の数: {len(stepwise_vars)-1} ---')
    # 選択変数から１変数を除外して回帰分析を実行
    for var in stepwise_vars:
        # 回帰分析する変数群から１変数を除外
        trial_vars = stepwise_vars[~(stepwise_vars == var)]
        X_trial = X[trial_vars]
        # 回帰分析の実行
        result = exec_linear_regression_sm(X_trial, y)
        print(result)
        # 除外変数の更新
        if drop_col == None:
            drop_col = var
            drop_aic = result['aic']
        elif result['aic'] < drop_aic:
            drop_col = var
            drop_aic = result['aic']
        # ベストなAICの場合、AIC・変数・回帰係数を保存
        if result['aic'] < best_aic:
            best_aic = result['aic']
            best_vars = result['vars']
            best_coefs = result['coef']
    # 最も悪いAICの変数を選択変数から除外する
    stepwise_vars = stepwise_vars[~(stepwise_vars == drop_col)]
    print(' ※除外変数: ', drop_col)

## ベストAICの変数を表示
print('\n--- best ---')
print('best AIC  : ', best_aic)
print('best vars : ', best_vars)
print('best coefs: ', best_coefs)

【実行結果】
一部見切れています。

AIC最小のベストモデルは、定数・X1・X2 の重回帰モデルでした。
回帰式で表現すると$${y = 621.426 + 11.858 x_1 - 5.973 x_2}$$です。

はじめて変数選択プログラムを自作しました。
何とか動いてくれてよかったです！

後から気づいたのですが、Stepwise法の実装は第６章「時系列 ARIMA モデル」の次数 p, d, q の最適値選択の実装によく似ています。

第２章の寄り道写経は以上です。

シリーズの記事

次の記事

前の記事

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルはＲ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。

この記事が参加している募集

#うちの積読を紹介する

1,881件

この記事が気に入ったらサポートをしてみませんか？