
第1章「チョコボールでエンゼルが当たる確率のベイズ推定」のベイズモデリングをPyMC Ver.5 で
たのしいベイズモデリング「2」へ
テキストが「たのしいベイズモデリング2」に変わります!
引き続き、新テキストのベイズモデルを PyMC Ver.5 で実験します。
さあ、次なる探検へ出発しましょう!

この記事は、テキスト「たのしいベイズモデリング2」の第1章「チョコボールでエンゼルが当たる確率のベイズ推定」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
この章では、森永製菓さんのお菓子「チョコボール」で金のエンゼル・銀のエンゼルが当たる確率について、ベイズモデルで推論します。
執筆ご担当の先生がインターネットで収集した「チョコボールデータ」をお借りして、PyMCモデリングを試みます。
心機一転、「2」を成功裏にスタートさせるべく、気合一番、ベイズモデリングに取り組みました。
がしかし、今回は収束を迎えることができませんでした(泣)

気を取り直して、さあ、PyMCのベイズモデリングを楽しみましょう。
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 武藤拓之 先生
モデル難易度: ★★★★★ (難しい)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★・・& そこそこ \\
結果再現度 & ★・・・・& NG!! \\
楽しさ & ★★★★★& 楽しい! \\
\end{array}
$$

評価ポイント
「チョコボールのエンゼルが当たる確率」という魅力的な題材を楽しむことができました!
第1章から収束させることができず、幸先の良いスタートを切ることができませんでした(汗)
工夫・喜び・反省
収束できない原因の箇所は「2次元の確率パラメータを与える多項分布」です。1次元の確率パラメータを与えると収束しました。
多次元のパラメータを扱う多変量確率分布モデルの場合、私の技量ではうまく動かせないことが多いです。
問題箇所が判っているのに、対策を掘り当てることができず、改善できない状態。ちょっぴり辛い。しかし、いつかは対策が見つかることを信じています。ただし、モデルの一部分だけを抜き出して収束させることはできました(粘ってみました)。
一部分のモデルを用いたベイズ流分析を堪能できたので、楽しさを満点にしました!

モデルの概要
テキストの調査・実験の概要
■ チョコボールとエンゼルたち
「チョコボール」でネット検索すると、エンゼルの当たりの確率を謳う記事が多数表示されます。
金・銀のエンゼルは国民的関心事なのです!
「チョコボール ベイズ」でネット検索すると、ベイズモデルで金・銀の当たる確率を推論した猛者たちの情報がちらほらと見られます。
金・銀のエンゼルが当たる確率を追究するのはベイジアンの本能なのです!

■ データの概要
先生は「チョコボールデータ」つまり金のエンゼル・銀のエンゼル・はずれの枚数の実地調査データをインターネットで集めて、全14標本、12,283箱を分析に用いています。
チョコボールのエンゼルを調査して、その上、調査記録をネットで公開した方々に感謝です!
■ 3つのケース:調査記録と確率分布の関係
先生がネットのエンゼル調査標本から類推したケースは次の3つ。
①あらかじめ箱の総数が決まっているケース
②金のエンゼルが1つ当たった時点で調査を打ち切るケース
③銀のエンゼルが当たった枚数を確認できない欠損値ケース
①のケースは、金・銀・はずれの枚数が、箱の総数を試行回数パラメータ、金・銀・はずれの確率を確率パラメータに用いる「多項分布」に従うと仮定します。
②のケースでは金の枚数は1であり、箱の総数が、金の確率を確率パラメータに用いる「幾何分布」に従うと仮定します。
また、銀の枚数が、「箱の総数-金の枚数1」を試行回数パラメータ、「銀・はずれの確率に占める銀の確率の比率」を確率パラメータに用いる「二項分布」に従うと仮定します。
③のケースは、②の打ち切りケースのうちの1標本が該当します。銀の枚数を推定できないため、②のケースの前半の「幾何分布」のみを仮定します。

■ 金のエンゼル2倍キャンペーンの考慮
2017年11月から2018年2月の期間には、金のエンゼルが当たる確率が2倍、ただし、銀のエンゼルは当たらないという、キャンペーンが実施されていたそうです。
このキャンペーン期間に該当する標本について、金・銀のエンゼルの当たる確率を求める際には、金の当たる確率を2倍(通常は1倍)、銀の当たる確率を0倍(通常は1倍)の重み付けをします。
$$
\begin{array}{c|cc}
エンゼル & 通常期間 & キャンペーン期間 \\
\hline
金 & 金の当たる確率 \times 1 & 金の当たる確率 \times 2 \\
銀 & 銀の当たる確率 \times 1 & 銀の当たる確率 \times 0 \\
\end{array}
$$
ここまでの説明を図示します。

テキストのモデリング
■目的変数と関心のあるパラメータ
目的変数はケースによって変動します。
①の箱の総数が決まっているケースでは、金のエンゼルの枚数$${N_{gold, i}}$$、銀のエンゼルの枚数$${N_{silvar, i}}$$、はずれの枚数$${N_{miss, i}}$$です。
②打ち切りケース・③銀の欠損値ケースでは、幾何分布にかかる部分は箱の総数$${N_{total, i}}$$です。
二項分布にかかる部分は銀のエンゼルの枚数$${N_{silvar, i}}$$です。
関心のあるパラメータはもちろん、当たりの確率です!
具体的には、金のエンゼルが当たる確率$${\theta_{gold, i}}$$、銀のエンゼルが当たる確率$${\theta_{silvar, i}}$$、はずれの確率$${\theta_{miss, i}}$$です。
なお、添字$${i}$$は標本IDです。
■ テキストのベイズモデル
【case ①箱の総数が決まっているケース】
$$
\begin{align*}
\boldsymbol{N}_i &\sim \text{Multinomial}\ (N_{total, i},\ \boldsymbol{p^*}_i) \\
ただし \\
\boldsymbol{N}_i &= \{ N_{gold, i},\ N_{silver, i},\ N_{miss, i} \} \\
\boldsymbol{p^*}_i &= \{ \theta^*_{gold, i},\ \theta^*_{silver, i},\ \theta^*_{miss, i} \} \\
&= \{ \theta_{gold, i} W_{gold, i},\ \theta_{silver, i} W_{silver, i},\ 1-(\theta_{gold, i} W_{gold, i} + \theta_{silver, i} W_{silver, i}) \} \\
W_{gold, i} &= \begin{cases} 1 & 通常期間 \\ 2 & キャンペーン期間\end{cases}
\\
W_{silver, i} &= \begin{cases} 1 & 通常期間 \\ 0 & キャンペーン期間\end{cases}
\end{align*}
$$
【case ②打ち切りケース】
$$
\begin{align*}
N_{total, i} &\sim \text{Geometric}\ (\theta^*_{gold, i}) \\
\text{if not} ③銀の&欠損値ケース \\
N_{silver, i} &\sim \text{Binomial}\ \left(N_{total, i} - 1,\ \cfrac{\theta^*_{silver, i}}{1- \theta^*_{gold, i}} \right) \\
\end{align*}
$$
【事前分布】
$$
\begin{align*}
\theta_{gold} &\sim \text{TruncatedBeta}\ (1,\ 101,\ \text{upper}=0.5) \\
\theta_{silver} &\sim \text{Uniform}\ (0,\ 0.5) \\
\end{align*}
$$
先生の経験値「100箱のチョコボールを開封しても金のエンゼルが1枚も当たらない」を取り入れて、金のエンゼルの確率$${\theta_{gold}}$$がパラメータ$${\alpha=1,\ \beta=101}$$のベータ分布に従うと仮定しています。
$${\text{Beta}(1, 101)}$$は$${\theta_{gold}}$$の事前分布を一様分布とした場合に100箱のチョコボールを開封して金のエンゼルが1枚も当たらないときの$${\theta_{gold}}$$の事後分布と一致するそうです(たぶん共役関係)。
また、金のエンゼルの当たる確率は50%未満という情報を加えて、上限0.5の切断ベータ分布にしています。
■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルは収束できず、分析に利用できない状況です。

PyMC実装
Let's enjoy PyMC & Python !
作戦
テキストのモデルに似せた「フルモデル」と収束を第一優先する「部分モデル」の2モデルを実践します!
準備・データ確認
1.インポート
### インポート
# ユーティリティ
import pickle
from pprint import pprint
# 数値・確率計算
import pandas as pd
import numpy as np
# PyMC
import pymc as pm
import pytensor.tensor as pt
import arviz as az
# 描画
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')2.データの読み込みと前処理
csvファイルをpandasのデータフレームに読み込みます。
### データの読み込み
data_orgn = pd.read_csv('angels_data.csv')
display(data_orgn)【実行結果】
全14行です。1行が1つ標本のデータです。
データ項目は次のとおりです。
・SampleID:標本ID
・N_Total:調査した箱の総数
・N_Gold:金のエンゼルが当たった枚数
・N_Silver:銀のエンゼルが当たった枚数
・N_Miss:はずれの枚数
・is_Censored:金のエンゼルが1枚当たったら調査を打ち切るケースが1
・is_Censored:キャンペーン期間に該当するケースが1

Rサンプルコードとほぼ同じ内容でデータの前処理をします。
### データの前処理
## データフレームのコピー
data = data_orgn.copy()
## 銀のエンゼルが欠損値の場合の前処理
# 欠損値を-999で埋める
data.fillna(-999, inplace=True)
# is_Silver_NaN列を追加(銀のエンゼル欠損値:1、それ以外:0)
data['is_Silver_NaN'] = np.where(data['N_Silver'] == -999, 1, 0)
## 金のエンゼル2倍キャンペーンを示す列の追加
# W_Gold列:金の倍数を追加(キャンペーン行・倍数:2、キャンペーン外の行・倍数:1)
data['W_Gold'] = np.where(data['is_Campaign'] == 1, 2, 1)
# W_Silver列:銀の倍数を追加(キャンペーン行・倍数:0、キャンペーン外の行・倍数:1)
data['W_Silver'] = np.where(data['is_Campaign'] == 1, 0, 1)
## 値の型を整数に変換
data = data.astype(int)
## 前処理後のデータフレームの表示
display(data)【実行結果】
W_Gold列、W_Silver列はキャンペーン期間を考慮した金・銀の当たる確率の重みです。

2.データの外観の確認
オリジナルデータの要約統計量を見てみます
### 要約統計量の表示
data_orgn.describe().round(2)【実行結果】
開けた箱の数の平均は877個。大量のチョコボールを食べたのですね!
金のエンゼルの枚数の平均は0.5枚、高き門です。
銀のエンゼルの枚数の平均は27枚で、金の約54倍です。
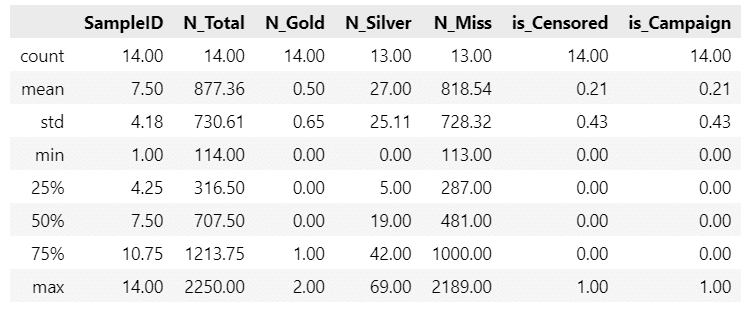
各標本の金・銀の割合を見てみます。
### 各標本の金・銀のエンゼルの割合の表示
# data_orgnから総枚数~はずれ枚数をコピー
tmp = data_orgn.iloc[:, 1:5]
# 各枚数を総枚数で除算
tmp = (tmp.T * 100 / tmp['N_Total']).T.iloc[:, 1:]
# データフレームの列名とインデックスの名前を設定
tmp.columns = ['金', '銀', 'はずれ']
tmp.index.name = '標本ID'
# 表示
display(tmp.round(2))【実行結果】
金のエンゼルの割合が最も高いのは標本2 の 0.88%。
標本12は金も銀も当たっていません。

全標本による金・銀の当たる確率(平均値)を見てみましょう。
### 各標本の金・銀のエンゼルの割合の表示 ※欠損値を外しており合計は100%にならない
# data_orgnから総枚数~はずれ枚数を合計を算出
tmp = data_orgn.iloc[:, 1:5].sum()
# 総枚数で除算して割合(%)を算出
tmp = (tmp * 100 / tmp['N_Total']).to_frame().T.iloc[:, 1:]
# データフレームの列名を設定
tmp.columns = ['金', '銀', 'はずれ']
tmp.rename(index={0: '%'}, inplace=True)
# 表示
display(tmp.round(2))【実行結果】
金のエンゼルの確率(平均値)は 0.06%。やはり高き門です。
銀のエンゼルの確率(平均値)は 2.86%。大人買いすれば1枚くらいは当たりそうです。
なお、欠損値を除いていますので、3つの確率(平均値)の合計は 100% になりません。

棒グラフで各標本の当たり具合を確認しましょう。
### 標本ごとの積み上げ棒グラフの描画
## 描画用データ加工
# dataのコピー取得
tmp = data.copy()
# 欠損値の-999を0に置き換え
tmp.loc[tmp['N_Silver']==-999, ['N_Silver', 'N_Miss']] = [0, 0]
# 欠損値データの「ハズレまたは銀」の枚数を計算
tmp['N_Sil_Mis'] = tmp['N_Total'] - tmp['N_Gold'] - tmp['N_Silver'] - tmp['N_Miss']
# 列の並び順を整理、データフレームの完成
tmp = tmp[['SampleID', 'N_Miss', 'N_Sil_Mis', 'N_Silver', 'N_Gold']]
## 描画
# 色順の設定
colors = ['lightpink', 'thistle', 'darkgray', 'chocolate']
# ハズレ~金の枚数を棒グラフに積み上げ
fig, ax = plt.subplots(figsize=(10, 8))
for i in range(1, len(tmp.columns)):
# 棒グラフの描画 ※leftに設定する値が積み上げのスタート地点になる
ax.barh(tmp['SampleID'], tmp.iloc[:, i], left=tmp.iloc[:, 1:i].sum(axis=1),
color=colors[i-1])
# 修飾
ax.set(xlabel='枚数', ylabel='標本ID', yticks=(range(1, len(tmp)+1)))
ax.grid(lw=0.5, ls='--')
# 凡例を横並びにしてグラフの外に出す
ax.legend(['ハズレ', 'ハズレor銀', '銀のエンゼル', '金のエンゼル'],
ncols=4, bbox_to_anchor=(0, 1), loc='lower left')
plt.show()【実行結果】
金のエンゼルはほぼ見えません・・・


モデル構築 フルモデル
作戦
Stanでは$${変数\alpha[0]=\text{Normal}(\cdots)}$$のように、スライスした変数に代入することができるようです。この記述ができることで、if文と併用して、観測データのケース(箱の総数が予め決まっているケース、打ち切りケースなど)に応じて柔軟に数式を定義できるようです。
しかしPyMCの初学者には、変数に用いられるPyTensorのテンソル等へ柔軟に値を代入するコードを書けません。スライスした変数に代入するコード作成ぶ困難を感じているのです。
そこで、観測値を3つのケースに分割して、ケース単位で尤度関数と必要な変数を作成する作戦を取りました。
つまり、モデルの定義が長~くなります。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
4段表示の1段目は興味のあるパラメータ「金・銀・はずれ」の確率の事前分布です。
2段目は①あらかじめ箱の総数が決まっているケースの計算値および尤度です。
3段目は②金のエンゼルが1つ当たった時点で調査を打ち切るケースの計算値および尤度です。
4段目は③銀のエンゼルが当たった枚数を確認できない欠損値ケースの計算値および尤度です。
$$
\begin{align*}
\theta_{gold} &\sim \text{TruncatedBeta}\ (\text{alpha}=1,\ \text{beta}=101,\ \text{lower}=0,\ \text{upper}=0.5) \\
\theta_{silver} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=0.5) \\
\theta_{miss} &= 1 - \theta_{gold} - \theta_{silver} \\
\\
p^*_{gold\_noncens} &= \theta_{gold} \times W_{gold\_noncens} \\
p^*_{silver\_noncens} &= \theta_{silver} \times W_{solver\_noncens} \\
p^*_{miss\_noncens} &= 1 - p^*_{gold\_noncens} - p^*_{silver\_noncens} \\
\boldsymbol{p}^*_{noncens} &= [p^*_{gold\_noncens},\ p^*_{silver\_noncens},\ p^*_{miss\_noncens}] \\
likelihood_{\boldsymbol{N}_{noncens}} &\sim \text{Multinomial}\ (\text{n}=N_{total\_noncens},\ \text{p}=\boldsymbol{p}^*_{noncens}) \\
\\
p^*_{gold\_cens} &= \theta_{gold} \times W_{gold\_cens} \\
p^*_{silver\_cens} &= \theta_{silver} \times W_{solver\_cens} \\
likelihood_{N_{total\_cens}} &\sim \text{Geometric}\ (\text{p}=p^*_{gold\_cens}) \\
likelihood_{N_{silver\_cens}} &\sim \text{Binomial}\ (\text{n}=N_{total\_cens},\ \text{p}=p^*_{silver\_cens}/(1-p^*_{gold\_cens})) \\
\\
p^*_{gold\_nan} &= \theta_{gold} \times W_{gold\_nan} \\
likelihood_{N_{total\_nan}} &\sim \text{Geometric}\ (\text{p}=p^*_{gold\_nan}) \\
\end{align*}
$$

1.モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義
## データの前処理
# 箱の数が予め決まっているケース用のデータ
non_cens = data.query('is_Censored==0 & is_Silver_NaN==0').reset_index()
# 金のエンゼルを1枚当てたら調査を打ち切るケース用のデータ
cens = data.query('is_Censored==1 & is_Silver_NaN==0').reset_index()
# 銀のエンゼルが欠損値のケース用のデータ
nan = data.query('is_Silver_NaN==1').reset_index()
## モデルの定義
with pm.Model() as model:
###### 全データ共通の定義
## coordの定義
# ラベルの種類
model.add_coord('kind', values=['金', '銀', '無'], mutable=True)
## 事前分布
# 金の割合θgold:切断ベータ分布
betaDist = pm.Beta.dist(alpha=1, beta=101)
thetaGold = pm.Truncated('thetaGold', dist=betaDist, lower=0, upper=0.5)
# 銀の割合θsilver:一様分布
thetaSilver = pm.Uniform('thetaSilver', lower=0, upper=0.5)
###### 箱の総数が予め決まっている標本のモデル(11)
## coordの定義
# データのインデックス
model.add_coord('dataNonCens', values=non_cens.index, mutable=True)
## dataの定義
# 金の倍率データ(キャンペーン時:2、その他:1)
wGoldNonCens = pm.ConstantData(
'wGoldNonCens', value=non_cens['W_Gold'].values, dims='dataNonCens')
# 銀の倍率データ(キャンペーン時:0、その他:1)
wSilverNonCens = pm.ConstantData(
'wSilverNonCens', value=non_cens['W_Silver'].values, dims='dataNonCens')
# 総枚数データ
nTotalNonCens = pm.ConstantData(
'nTotalNonCens', value=non_cens['N_Total'].values, dims='dataNonCens')
# 観測値(金・銀・はずれの枚数)
obsNonCens = pm.ConstantData(
'obsNonCens', value=non_cens[['N_Gold', 'N_Silver', 'N_Miss']].values,
dims=('dataNonCens', 'kind'))
## 計算値
# p*gold: θgoldキャンペーンの重みを反映
pStarGoldNonCens = thetaGold * wGoldNonCens
# p*silver: θsilverキャンペーンの重みを反映
pStarSilverNonCens = thetaSilver * wSilverNonCens
# p*missの割合の算出
pStarMissNonCens = 1 - pStarGoldNonCens- pStarSilverNonCens
# p*をshape=(データ個数, 金・銀・はずれの種類)に2次元化
pStarNonCens = pt.stack([pStarGoldNonCens, pStarSilverNonCens,
pStarMissNonCens]).T
## 尤度
# 多項分布:金・銀・はずれが主体
likeNonCensNumAll = pm.Multinomial(
'likeNonCensNumAll', n=nTotalNonCens, p=pStarNonCens,
observed=obsNonCens, dims=('dataNonCens', 'kind'))
###### 金のエンゼルが1枚当たって調査を打ち切った標本のモデル(2)
## coordの定義
# データのインデックス
model.add_coord('dataCens', values=cens.index, mutable=True)
## dataの定義
# 金の倍率データ(キャンペーン時:2、その他:1)
wGoldCens = pm.ConstantData(
'wGoldCens', value=cens['W_Gold'].values, dims='dataCens')
# 銀の倍率データ(キャンペーン時:0、その他:1)
wSilverCens = pm.ConstantData(
'wSilverCens', value=cens['W_Silver'].values, dims='dataCens')
# 銀の枚数データ
nSilverCens = pm.ConstantData(
'nSilverCens', value=cens['N_Silver'].values, dims='dataCens')
# 総枚数データ
nTotalCens = pm.ConstantData(
'nTotalCens', value=cens['N_Total'].values, dims='dataCens')
## 計算値
# p*gold: θgoldキャンペーンの重みを反映
pStarGoldCens = thetaGold * wGoldCens
# p*silver: θsilverキャンペーンの重みを反映
pStarSilverCens = thetaSilver * wSilverCens
## 尤度
# 金が当たる(成功する)まで試行を繰り返す幾何分布:金が主体
likeCensNumTotal = pm.Geometric(
'likeCensNumTotal', p=pStarGoldCens, observed=nTotalCens,
dims='dataCens')
# 銀が当たる二項分布:銀が主体
likeCensNumSilver = pm.Binomial(
'likeCensNumSilver', n=nTotalCens-1,
p=pStarSilverCens/(1-pStarGoldCens),
observed=nSilverCens, dims='dataCens')
###### 銀のエンゼルに欠損値がある標本のモデル:打ち切りモデル(1)
## coordの定義
# データのインデックス
model.add_coord('dataNan', values=nan.index, mutable=True)
## dataの定義
# 金の倍率データ(キャンペーン時:2、その他:1)
wGoldNan = pm.ConstantData(
'wGoldNan', value=nan['W_Gold'].values, dims='dataNan')
# 総枚数データ
nTotalNan = pm.ConstantData(
'nTotalNan', value=nan['N_Total'].values, dims='dataNan')
## 計算値
# p*gold: θgoldキャンペーンの重みを反映
pStarGoldNan = thetaGold * wGoldNan
## 尤度
# 幾何分布:金が主体
likeNanNumTotal = pm.Geometric(
'likeNanNumTotal', p=pStarGoldNan, observed=nTotalNan, dims='dataNan')
### 計算値
thetaMiss = pm.Deterministic('thetaMiss', 1 - thetaGold - thetaSilver)
ratio = pm.Deterministic('ratio', thetaSilver / thetaGold)【モデル注釈】省略
2.モデルの外観の確認
# モデルの表示
model【実行結果】
途中の計算値をDeterministic変数にしなかったので、シンプルな構造に見えます。

# モデルの可視化
pm.model_to_graphviz(model)【実行結果】
左の縦列は①箱の総数が予め決まっているケース、中央右列は②打ち切りケース、最右列は③銀の欠損値のケースです。
推論するパラメータは中央左の2つの楕円「thetaGold $${\theta_{gold}}$$、thetaSilver $${\theta_{silver}}$$」です。

3.事後分布からのサンプリング
乱数生成数はテキストよりも少なくしています。
発散防止の目的でtarget_acceptを高い値にしています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ30秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 30秒
# テキストは iter=250500, warmup=500, chains=4, thin=1
with model:
idata = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.998,
nuts_sampler='numpyro', random_seed=123)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
全てのパラメータが$${\hat{R} > 1.1}$$になりました(実行結果が$${\neq 0}$$)。
収束条件を満たさない事態です(汗)

分布が収束していませんので、ここからのコードは事後分布データの状況把握のために実行します。
まずはざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
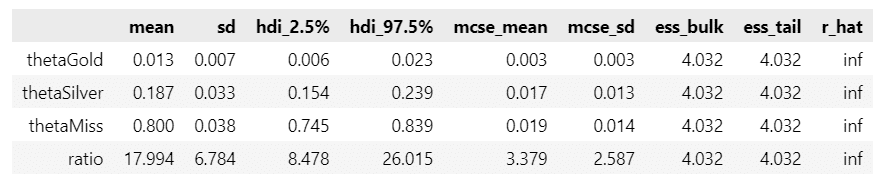
pm.summary(idata, hdi_prob=0.95, round_to=3)【実行結果】
$${\hat{R}}$$の値が inf (無限大)になっています。
ess_bulkやess_tailの値は低く、モデリング精度が高くなさそうです。
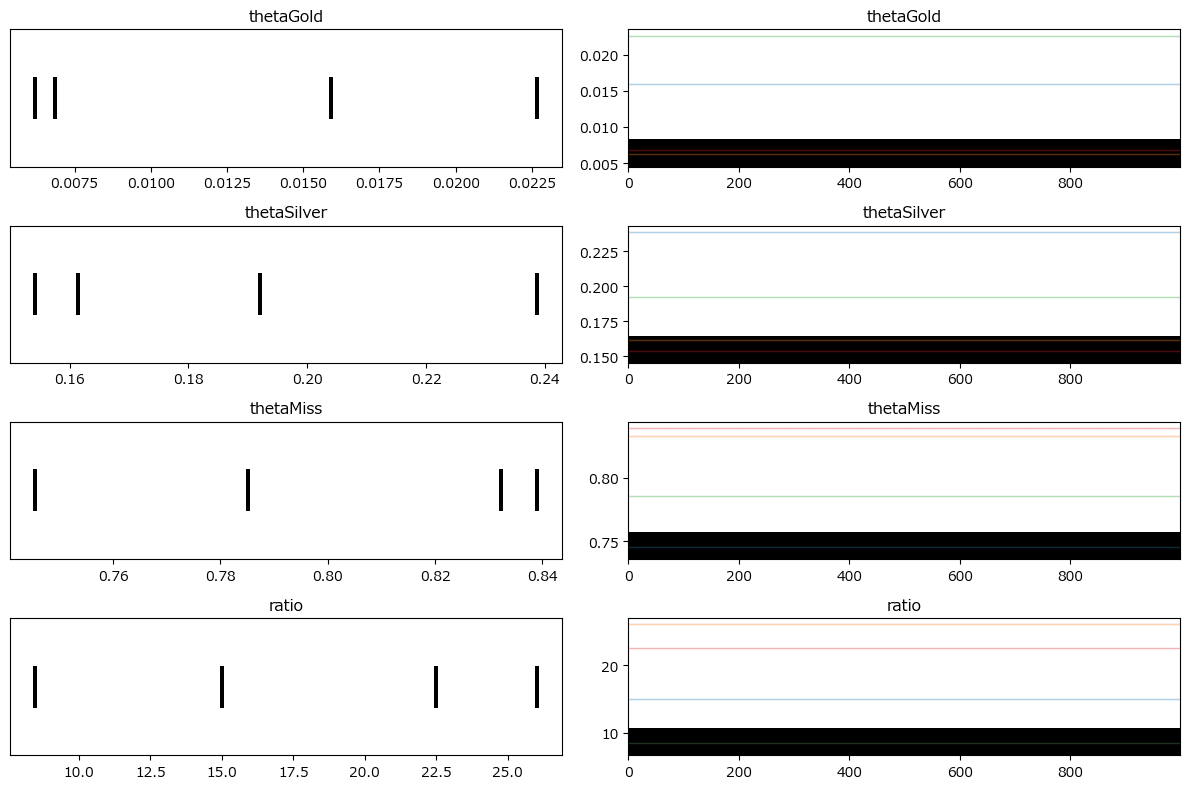
### トレースプロットの表示
pm.plot_trace(idata, compact=False)
plt.tight_layout();【実行結果】
左側のグラフでは、4本の線がバラバラに立っています。
4つのチェーンがそれぞれバラバラの推論、しかも、分布の広がりのないほぼ単一値を返しているようです。
右側のグラフではカラーの線に乱雑さがみられません。また、下に黒帯のような発散だらけの状況が示されています。
5.分析~モデルの問題点
このモデルを用いたデータ分析は断念します。
次の一部モデルでデータ分析を試みる予定です。
ここでは、収束しない問題点について考えてみます。
次のコード「①あらかじめ箱の総数が決まっているケースの尤度である多項分布」の記述箇所が、なにか悪さをしている感じです。
# 多項分布:金・銀・はずれが主体
likeNonCensNumAll = pm.Multinomial(
'likeNonCensNumAll', n=nTotalNonCens, p=pStarNonCens,
observed=obsNonCens, dims=('dataNonCens', 'kind'))確率パラメータ$${p}$$に設定した変数 pStarNonCens は1次元目:標本データ数(11件)、2次元目:金・銀・はずれの種類数(3件)の2次元です。
標本ごとに金・銀・はずれの確率(キャンペーン重み付け後)を設定しています。
この確率パラメータに1次元の確率「金・銀・はずれの確率」を設定してMCMCを行うと、なんと収束します!
なぜか確率を2次元にすると収束しません。
収束しない理由にたどり着くことは、現時点では困難です(スキル不足)。
問題点の掘り下げは以上で終了です。
フルモデルでは収束できす、分析を着手できませんでした。
そこで「一部モデル」の登場です。収束を狙っていきます!
6.推論データ(idata)の保存
推論データを再利用する(?)場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idataの保存 pickle
file = r'idata_ch01.pkl'
with open(file, 'wb') as f:
pickle.dump(idata, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_ch01.pkl'
with open(file, 'rb') as f:
idata_load = pickle.load(f)
モデル構築 一部モデル
作戦
フルモデルで収束させられなかった「2次元パラメータの多項分布」を用いる①のケースを除外してモデル化します。
つまり、②金のエンゼルが1つ当たった時点で調査を打ち切るケース、③銀のエンゼルが当たった枚数を確認できない欠損値ケースの2つのケースに限定してモデリングします。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
フルモデルの数式から①あらかじめ箱の総数が決まっているケースの部分を除外しました。
3段表示の1段目は興味のあるパラメータ「金・銀・はずれ」の確率の事前分布です。
2段目は②金のエンゼルが1つ当たった時点で調査を打ち切るケースの計算値および尤度です。
3段目は③銀のエンゼルが当たった枚数を確認できない欠損値ケースの計算値および尤度です。
$$
\begin{align*}
\theta_{gold} &\sim \text{TruncatedBeta}\ (\text{alpha}=1,\ \text{beta}=101,\ \text{lower}=0,\ \text{upper}=0.5) \\
\theta_{silver} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=0.5) \\
\theta_{miss} &= 1 - \theta_{gold} - \theta_{silver} \\
\\
p^*_{gold\_cens} &= \theta_{gold} \times W_{gold\_cens} \\
p^*_{silver\_cens} &= \theta_{silver} \times W_{solver\_cens} \\
likelihood_{N_{total\_cens}} &\sim \text{Geometric}\ (\text{p}=p^*_{gold\_cens}) \\
likelihood_{N_{silver\_cens}} &\sim \text{Binomial}\ (\text{n}=N_{total\_cens},\ \text{p}=p^*_{silver\_cens}/(1-p^*_{gold\_cens})) \\
\\
p^*_{gold\_nan} &= \theta_{gold} \times W_{gold\_nan} \\
likelihood_{N_{total\_nan}} &\sim \text{Geometric}\ (\text{p}=p^*_{gold\_nan}) \\
\end{align*}
$$

1.モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義 ※打ち切りケースのみ(標本6,8,9)
## データの前処理
# 金のエンゼルを1枚当てたら調査を打ち切るケース用のデータ
cens = data.query('is_Censored==1 & is_Silver_NaN==0').reset_index()
# 銀のエンゼルが欠損値のケース用のデータ
nan = data.query('is_Silver_NaN==1').reset_index()
## モデルの定義
with pm.Model() as model2:
###### 全データ共通の定義
## coordの定義
# ラベルの種類
model2.add_coord('kind', values=['金', '銀', '無'], mutable=True)
## 事前分布
# 金の割合θgold:打ち切りベータ分布
betaDist = pm.Beta.dist(alpha=1, beta=101)
thetaGold = pm.Truncated('thetaGold', dist=betaDist, lower=0, upper=0.5)
# 銀の割合θsilver:一様分布
thetaSilver = pm.Uniform('thetaSilver', lower=0, upper=0.5)
###### 金のエンゼルが1枚当たって調査を打ち切った標本のモデル(2)
## coordの定義
# データのインデックス
model2.add_coord('dataCens', values=cens.index, mutable=True)
## dataの定義
# 金の倍率データ(キャンペーン時:2、その他:1)
wGoldCens = pm.ConstantData(
'wGoldCens', value=cens['W_Gold'].values, dims='dataCens')
# 銀の倍率データ(キャンペーン時:0、その他:1)
wSilverCens = pm.ConstantData(
'wSilverCens', value=cens['W_Silver'].values, dims='dataCens')
# 銀の枚数データ
nSilverCens = pm.ConstantData(
'nSilverCens', value=cens['N_Silver'].values, dims='dataCens')
# 総枚数データ
nTotalCens = pm.ConstantData(
'nTotalCens', value=cens['N_Total'].values, dims='dataCens')
## 計算値
# p*gold: θgoldキャンペーンの重みを反映
pStarGoldCens = thetaGold * wGoldCens
# p*silver: θsilverキャンペーンの重みを反映
pStarSilverCens = thetaSilver * wSilverCens
## 尤度
# 金が当たる(成功する)まで試行を繰り返す幾何分布:金が主体
likeCensNumTotal = pm.Geometric(
'likeCensNumTotal', p=pStarGoldCens, observed=nTotalCens,
dims='dataCens')
# 銀が当たる二項分布:銀が主体
likeCensNumSilver = pm.Binomial(
'likeCensNumSilver', n=nTotalCens-1,
p=pStarSilverCens/(1-pStarGoldCens),
observed=nSilverCens, dims='dataCens')
###### 銀のエンゼルに欠損値がある標本のモデル:打ち切りモデル(1)
## coordの定義
# データのインデックス
model2.add_coord('dataNan', values=nan.index, mutable=True)
## dataの定義
# 金の倍率データ(キャンペーン時:2、その他:1)
wGoldNan = pm.ConstantData(
'wGoldNan', value=nan['W_Gold'].values, dims='dataNan')
# 総枚数データ
nTotalNan = pm.ConstantData(
'nTotalNan', value=nan['N_Total'].values, dims='dataNan')
## 計算値
# p*gold: θgoldキャンペーンの重みを反映
pStarGoldNan = thetaGold * wGoldNan
## 尤度
# 幾何分布:金が主体
likeNanNumTotal = pm.Geometric(
'likeNanNumTotal', p=pStarGoldNan, observed=nTotalNan, dims='dataNan')
###### 計算値
thetaMiss = pm.Deterministic('thetaMiss', 1 - thetaGold - thetaSilver)
ratio = pm.Deterministic('ratio', thetaSilver / thetaGold)【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の3つを設定しました。金・銀・はずれの識別ラベル:名前「kind」、値「金・銀・空」
②打ち切りデータの行の座標:名前「dataCens」、値「行インデックス」
③銀の欠損値データの行の座標:名前「dataNan」、値「行インデックス」
dataの定義
観測データの変数を多数活用するので、dataの定義も多くなりました。打ち切りデータ
銀の当たり枚数$${nSilverCens}$$、総枚数(開けた箱数)$${nTotalCens}$$
キャンペーンによる重み付け:金の倍率$${wGoldCens}$$、銀の倍率$${wSilverCens}$$
銀の欠損値データ
総枚数(開けた箱数)$${nTotalNan}$$
キャンペーンによる重み付け:金の倍率$${wGoldNan}$$
パラメータの事前分布
金の当たる確率$${thetaGold}$$
pm.Beta.dist()でベータ分布を指定して、pm.Truncated()で切断の下端 0、上端 0.5を指定銀の当たる確率$${thetaSilver}$$
0から0.5を区間とする一様分布pm.Uniform()を指定
尤度
打ち切りデータ
金が当たるまで試行を繰り返す幾何分布
「全枚数-金の枚数1」のうち銀が当たる枚数が従う二項分布
銀の欠損値データ
金が当たるまで試行を繰り返す幾何分布
2.モデルの外観の確認
# モデルの表示
model2【実行結果】
途中の計算値をDeterministic変数にしなかったので、シンプルな構造に見えます。

# モデルの可視化
pm.model_to_graphviz(model2)【実行結果】
左の縦列は②打ち切りケース(標本数2)、右の縦列は③銀の欠損値のケース(標本数1)です。
少量のデータでも推論できるのがベイズの凄いところです!
推論するパラメータは中央の2つの楕円「thetaGold $${\theta_{gold}}$$、thetaSilver $${\theta_{silver}}$$」です。

3.事後分布からのサンプリング
乱数生成数はテキストよりも少なくしています。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ20秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 20秒
# テキストは iter=250500, warmup=500, chains=4, thin=1
with model2:
idata2 = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.8,
nuts_sampler='numpyro', random_seed=123)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認は高めに設定して、$${\hat{R} \leq 1.01}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata2 # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.01}$$であることを確認できました。
収束できてよかったです!

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata2, hdi_prob=0.95, round_to=4)【実行結果】
平均(mean)の欄に金・銀・はずれの確率の平均値が掲載されています。
金:0.09%、銀:3.24%、はずれ:96.67%。
金は超難関ですね。

### トレースプロットの表示
pm.plot_trace(idata2, compact=False)
plt.tight_layout();【実行結果】
右のグラフでは線がまんべんなく行き来しています。収束の傾向です。
左のグラフでは4つ(4色)の事後分布サンプリングデータがほぼ同じ形状をしています。推論がうまくいっている傾向です!

5.分析~テキストにならって
金のエンゼル・銀のエンゼル・はずれの各確率を確認しましょう!
これらの事後分布について、テキスト図1.2に相当するグラフを描画します。
テキストによると事後分布が左右対称になるとは限らないため点推定にMAP(最大事後確率)を用いるとしています。
そこで、PyMCのMAP算出に挑戦してみます(初出しです)。
### MAPの算出
map_data = pm.find_MAP(model=model2, seed=123)
pprint(map_data)【実行結果】
下の辞書型に各パラメータのMAPが掲載されています。

テキストの図1.2の描画に取り組みましょう。
### エンゼルが当たる確率に関するパラメータの事後分布の描画 ※図1.2に相当
## 初期値設定
# 利用するパラメータ
params = ['thetaGold', 'thetaSilver', 'thetaMiss']
# グラフタイトル
titles = ['金のエンゼルが当たる確率', '銀のエンゼルが当たる確率',
'いずれのエンゼルも当たらない確率']
## 描画
# 描画領域の指定
fig, ax = plt.subplots(3, 1, figsize=(8, 6))
# 3つのパラメータごとに統計量算出とヒストグラム描画を繰り返し処理
for i, (param, title) in enumerate(zip(params, titles)):
## パラメータの事後分布サンプリングデータを取得
sample = idata2.posterior[param].data.flatten()
## 統計量の算出
# MAP
MAP = map_data[param]
# 95%HDI
hdi95 = az.hdi(sample, hdi_prob=0.95)
# 99%HDI
hdi99 = az.hdi(sample, hdi_prob=0.99)
## 描画
# ヒストグラムの描画
sns.histplot(sample, bins=50, kde=True, stat='density', ec='white',
ax=ax[i])
# 中央値の垂直線の描画
ax[i].axvline(MAP, color='red', lw=2, label=f'MAP={MAP:.2%}')
# 95%HDIの下端・上端の垂直線の描画
ax[i].axvline(hdi95[0], color='red', ls='--',
label=f'95%HDI=[{hdi95[0]:.2%}, {hdi95[1]:.2%}]')
ax[i].axvline(hdi95[1], color='red', ls='--',)
# 99%HDIの下端・上端の垂直線の描画
ax[i].axvline(hdi99[0], color='red', ls=':',
label=f'99%HDI=[{hdi99[0]:.2%}, {hdi99[1]:.2%}]')
ax[i].axvline(hdi99[1], color='red', ls=':')
# 修飾:x軸目盛りの値を%化、凡例の表示
ax[i].xaxis.set_major_formatter(mpl.ticker.PercentFormatter(1.0))
ax[i].legend()
plt.tight_layout();【実行結果】
金・銀・はずれの確率の参考値は凡例に記載されています。
あくまで3つ標本からの推論であり、真の確率ではないことに留意しましょう。
テキストのMAP、HDI区間に近い推論が得られたと思います。
ただし、標本の数を減らしているからか、HDI区間はテキストよりも広くなっています。

続いてテキストの図1.3の作図に移ります。
銀のエンゼルは金のエンゼルの何倍当たりやすいかの推論結果を上の図の形式で可視化します。
当たりやすさの推論は model2 内の変数 ratio で定義して、MCMCで乱数を取得しています。
なお、MAPの値が適切ではない感じがしたので、中央値を表記しました。
### 金と銀のエンゼルが当たる確率の比の事後分布 ※図1.3に相当
## 倍率ratioの事後分布サンプリングデータを取得
sample = idata2.posterior.ratio.data.flatten()
## 統計量の算出
# 中央値
median = np.median(sample)
# 95%HDI
hdi95 = az.hdi(sample, hdi_prob=0.95)
# 99%HDI
hdi99 = az.hdi(sample, hdi_prob=0.99)
## 描画
# 描画領域の指定
plt.figure(figsize=(8, 2))
# ヒストグラムの描画
sns.histplot(sample, bins=100, kde=True, stat='density', ec='white')
# 中央値の垂直線の描画
plt.axvline(MAP, color='red', lw=2, label=f'中央値={median:.1f}')
# 95%HDIの下端・上端の垂直線の描画
plt.axvline(hdi95[0], color='red', ls='--',
label=f'95%HDI=[{hdi95[0]:.1f}, {hdi95[1]:.1f}]')
plt.axvline(hdi95[1], color='red', ls='--',)
# 99%HDIの下端・上端の垂直線の描画
plt.axvline(hdi99[0], color='red', ls=':',
label=f'99%HDI=[{hdi99[0]:.1f}, {hdi99[1]:.1f}]')
plt.axvline(hdi99[1], color='red', ls=':')
# 修飾
plt.title('銀のエンゼルは金のエンゼルの何倍当たりやすいか')
plt.xlabel('倍')
plt.legend()
plt.show()【実行結果】
テキストよりも低い値になりました。
3標本の全てで金を当てていますが、全標本の中には金を当てていない標本があるので、テキストの方が倍率が高くなったのかもです。
また、500倍以上という外れ値的な事後分布サンプリングデータがある関係でしょうか、中央値は事後分布の峰から右へずれてしまっています。

最後に、テキストの表1.2にならって、銀のエンゼルの実測値と予測値を比べてみます。
銀の枚数の事後予測はPyMCでは行わず、NumPyで二項分布乱数を生成して代用しました。
また、PyMCを用いないでMAPを算出する方法が分からなかったので、テキストのMAPに代えて中央値を算出しました。
### 銀のエンゼルが当たった数の実測値と事後予測分布の平均値・HDI ※表1.2に相当
## 要約統計量算出関数の定義
def calc_stats2(x):
hdi95 = az.hdi(x, hdi_prob=0.95)
hdi99 = az.hdi(x, hdi_prob=0.99)
return np.hstack([np.median(x), hdi95, hdi99])
## 初期値設定
# 乱数生成器の設定
rng = np.random.default_rng(seed=123)
## 事後予測サンプリングデータを作成して要約統計量を算出
# 観測データから打ち切りケースを取り出し
cens_df = data_orgn.query('is_Censored==1').reset_index(drop=True)
# 事後分布データから銀のエンゼルが当たる確率のサンプリングデータを取り出し
theta_silver = idata2.posterior.thetaSilver.data.flatten()
# 一時リストの初期化
stats_list = []
# 3つの標本について事後予測サンプリング・要約統計量の算出を繰り返し処理
for i in range(len(cens_df)):
# 銀のエンゼルの枚数について事後予測サンプリングを実行(二項分布乱数生成)
post_pred_silver = rng.binomial(n=cens_df.iloc[i, 1], p=theta_silver)
# 事後予測サンプリングデータの要約統計量を算出
stats_val = calc_stats2(post_pred_silver)
# 一時リストに格納
stats_list.append(stats_val)
## データフレーム化
# 一時リストのデータをデータフレーム化
silver_df2 = pd.DataFrame(stats_list,
columns=['中央値', '95%HDI下端', '95%HDI上端','99%HDI下端', '99%HDI上端'])
# 標本IDと実測値列を追加
silver_df2['標本ID'] = cens_df['SampleID']
silver_df2['実測値'] = cens_df['N_Silver']
# 列の並べかえ
silver_df2 = silver_df2[['標本ID','実測値', '中央値', '95%HDI下端', '95%HDI上端',
'99%HDI下端', '99%HDI上端']]
# データフレームの表示
display(silver_df2)
【実行結果】
まあまあテキストの事後予測値に近いかな?という感じです。
標本ID:6,9の実測値は99%HDI区間に収まっています。
また銀の枚数が欠損値となっていた標本ID:8について、銀の枚数が推論されました。99%HDIに基づいて14~45枚の範囲だと推論できます。

6.推論データ(idata)の保存
推論データを再利用する場合に備えてファイルに保存しましょう。
idataをpickleで保存します。
### idataの保存 pickle
file = r'idata2_ch01.pkl'
with open(file, 'wb') as f:
pickle.dump(idata2, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata2_ch01.pkl'
with open(file, 'rb') as f:
idata2_load = pickle.load(f)以上で第1章は終了です。

おわりに
金のエンゼル、銀のエンゼル
みなさんは金・銀のエンゼルをゲットした経験がありますか?
私は金も銀も当てたことがありません。
銀のエンゼルを目にしたことが1、2度ある程度です。
子供の頃はおもちゃの缶詰に憧れました。無い物ねだりですね。
今は「希少なくちばし」を手にしてみたい、という当てることへの関心のほうが大きいです。

シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
