
Python Panda3Dライブラリで火星の逆行を謎を解く
この記事は著者が作成したものです。日経ソフトウエア様のご承諾をいただき、著者の責任において作成・公開しています。
宇宙の謎を解き明かそうとする人類の歴史は、数々の理論と発見で彩られています。特に、地球を中心とする「天動説」から太陽を中心とする「地動説」への転換は、科学史における大きな転機となりました。漫画・アニメ『チ。』でも取り上げられているように、この理論の変遷は天体の動き、とりわけ火星の逆行現象の解釈に深く関わっています。
『チ。』の中で、バデーニがオクジーに対して地動説を説明する場面があります。バデーニを火星、オクジーを地球に見立てて円運動をすることで、オクジー(地球)がバデーニ(火星)を追い越す際に、バデーニが逆方向に動いて見えることを示します。このシーンは、火星の逆行現象を直感的に理解するのに非常に効果的です。
本記事では、このシーンを3Dアニメーションで精密に再現します。まず、地球と火星の公転半径と公転周期を基に、それぞれの公転速度を計算します。次に、太陽を中心とした「地動説」のモデルで両惑星の動きをアニメーション化し、進行方向を示す速度ベクトルを表示します。最後に、地球を中心とした「天動説」のモデルに切り替え、火星の速度ベクトルと地球の逆向き速度ベクトルを合成することで、火星の逆行現象を視覚的に解説します。
元となる雑誌記事の紹介
この記事は、日経ソフトウエア特集記事「Pythonで太陽系シミュレータを作る」を元に、小規模な改造で「天動説」を実現しています。この記事の内容を実際に試してみたい方は、次に紹介する雑誌をお買い求めください。
↓↓↓特集3 Pythonで「太陽系シミュレーター」を作る↓↓↓
この雑誌記事は、次のムックにも収録されています。
↓↓↓第9章 Pythonで「太陽系シミュレーター」を作る↓↓↓
第1章:地球と火星の公転速度の計算
火星の逆行を正確に表現するためには、地球と火星の動きを速度ベクトルとして視覚的に示すことが重要です。その準備として、まず地球と火星の公転速度を正しく計算します。
1.1 地球と火星の基本情報の紹介
最初に、地球と火星の公転半径と公転周期などの基本データを確認します。惑星の公転速度を計算するには、公転半径と公転周期の正確な数値が必要です。
地球
公転半径(太陽からの平均距離):約149,600,000 km
公転周期:約365.25日
火星
公転半径(太陽からの平均距離):約227,940,000 km
公転周期:約687日
1.2 公転速度の計算方法の説明
惑星の公転速度は、円軌道を仮定した場合、以下の式で計算できます。
$$
v= \frac{2\pi r}{T}
$$
v:公転速度(km/s)
r:公転半径(km)
T:公転周期(秒)
注意:公転周期は日単位で与えられているため、秒に換算します。
1.3 地球と火星の公転速度の具体的な計算
地球の公転速度
公転半径: $${r_{\text{地球}} = 149,600,000 \text{ km}}$$
公転周期: $${T_{\text{地球}} = 365.25 \text{ 日} \times 24 \text{ 時間} \times 3600 \text{ 秒} = 31,557,600 \text{ 秒}}$$
公転速度の計算: $${v_{\text{地球}} = \frac{2\pi \times 149,600,000}{31,557,600} \approx 29.78 \text{ km/s}}$$
火星の公転速度
公転半径:$${r_{\text{火星}} = 227,940,000 \text{ km}}$$
公転周期: $${T_{\text{火星}} = 687 \text{ 日} \times 24 \text{ 時間} \times 3600 \text{ 秒} = 59,356,800 \text{ 秒}}$$
公転速度の計算: $${v_{\text{火星}} = \frac{2\pi \times 227,940,000}{59,356,800} \approx 24.13 \text{ km/s}}$$
1.4 計算結果のまとめ
地球の公転速度:約29.78 km/s
火星の公転速度:約24.13 km/s
公転速度の関係
公転速度は公転半径に比例し、公転周期に反比例します。これは以下の式で示されます。
$$
v = \frac{2\pi r}{T}
$$
この式から、同じ太陽系内であれば、公転半径が大きくなると速度も増加しますが、公転周期が長くなると速度は減少します。
相対的な公転速度の計算
地球の公転速度を1としたとき、火星の公転速度は以下のように計算できます。
$$
\frac{v_{\text{火星}}}{v_{\text{地球}}} = \frac{24.13}{29.78} \approx 0.81
$$
したがって、地球の公転速度を1とすると、火星の公転速度は約0.81となります。
速度差の解説
地球は火星よりも内側の軌道を持つため、公転速度が速くなります。この速度差により、地球は定期的に火星を追い越します。
観測への影響
地球が火星を追い抜く際、地球から見た火星の位置は一時的に逆方向に動いているように見えます。これが火星の逆行現象です。この現象を正確にシミュレートするために、次章では地動説に基づいた3Dアニメーションを作成し、速度ベクトルを視覚的に表示します。
第2章:地動説による3Dアニメーションの作成
ここからの作業を進めるには、太陽系シミュレーターが完成していることが前提となります。まだシミュレーターが未完成の方は、特集記事を参考に、まずそちらを仕上げてください。
では、改造を開始しましょう。
2.1 地動説アニメーションプログラムの実装
まず、既存の太陽系シミュレーターに対して、地球と火星の公転運動を視覚的に強調する改造を行います。修正するファイルは、以下の4つです。改造の方針は次の2つです。
表示する惑星を地球と火星のみに限定する
惑星の進行方向を視覚的に示すために、速度ベクトルを描画します。
初めに、src/planet_settings.pyを開いて、PLANET_DICT_LISTの項目のうち、地球と火星以外をコメントにします。こうすることで、表示する惑星が2つだけになります。
PLANET_DICT_LIST = [
# 名前、半径、公転半径、公転周期、惑星の色、軌跡の色、初期角度(1986年1月1日の位置)、惑星を表す識別子
# dict(name='Sun', radius=0.1, orbit_radius=0, orbit_period=1,
# color=(1, 1, 1), line_color=(0, 1, 1), heading=0, horizons_id=10),
# dict(name='Mercury', radius=0.383, orbit_radius=0.387, orbit_period=0.241,
# color=(0.5, 0.5, 0.5), line_color=(0, 1, 1), heading=221.783, horizons_id=199),
# dict(name='Venus', radius=0.949, orbit_radius=0.723, orbit_period=0.615,
# color=(1, 0.5, 0), line_color=(0, 1, 1), heading=269.983, horizons_id=299),
dict(name='Earth', radius=1.000, orbit_radius=1.000, orbit_period=1.000,
color=(0, 0, 1), line_color=(0, 1, 1), heading=100.469, horizons_id=399),
dict(name='Mars', radius=0.532, orbit_radius=1.524, orbit_period=1.881,
color=(1, 0, 0), line_color=(0, 1, 1), heading=189.549, horizons_id=499),
# dict(name='Jupiter', radius=11.209, orbit_radius=5.203, orbit_period=11.862,
# color=(0, 1, 0), line_color=(0, 1, 1), heading=325.363, horizons_id=599),
# dict(name='Saturn', radius=9.449, orbit_radius=9.537, orbit_period=29.457,
# color=(0.5, 0, 0.5), line_color=(0, 1, 1), heading=242.112, horizons_id=699),
# dict(name='Uranus', radius=4.007, orbit_radius=19.191, orbit_period=84.017,
# color=(0, 1, 1), line_color=(0, 1, 1), heading=258.660, horizons_id=799),
# dict(name='Neptune', radius=3.883, orbit_radius=30.069, orbit_period=164.791,
# color=(0, 0, 0.5), line_color=(0, 1, 1), heading=273.575, horizons_id=899),
]次に、src/geometry.pyを開いて、速度ベクトルを表す矢印を描画するスタティックメソッドを追記します。draw_velocity_arrowメソッドは、線と三角形を組み合わせて、速度を表す矢印を描画します。
# Geometryクラスに2つのスタティックメソッドを追記
@staticmethod
def draw_triangle(parent, point1, point2, point3, color):
"""三角形を描画する関数(面に色を付ける)"""
vertices = [point1, point2, point3]
# GeomVertexDataを作成
vdata = GeomVertexData('shape', GeomVertexFormat.getV3(), Geom.UHStatic)
vdata.setNumRows(len(vertices))
# GeomVertexWriterを使って頂点データを設定
vertex = GeomVertexWriter(vdata, 'vertex')
for v in vertices:
vertex.addData3f(*v)
# GeomTrianglesの場合、頂点を三つずつ追加
primitive = GeomTriangles(Geom.UHStatic)
primitive.addVertices(0, 1, 2)
primitive.closePrimitive()
# Geomを作成してGeomPrimitiveを追加
geom = Geom(vdata)
geom.addPrimitive(primitive)
# GeomNodeを作成してGeomを設定
node = GeomNode('triangle_node')
node.addGeom(geom)
# ノードパスを作成してシーンに追加
node_path = parent.attachNewNode(node)
node_path.setColor(*color) # 色を設定
node_path.setTwoSided(True) # 両面を描画
return node_path
@staticmethod
def draw_velocity_arrow(parent, velocity_length, color, head_size=1):
"""
線と三角形を組み合わせて、ベクトルを表す矢印を描画する関数
"""
if velocity_length <= 0:
return
if velocity_length > head_size:
# Draw the line representing the velocity
Geometry.draw_line_between_two_points(
Point3(velocity_length - head_size / 2, 0, 0), Point3(0, 0, 0), color, parent, thickness=4)
# Draw the first triangle
triangle1 = Geometry.draw_triangle(
parent, (0, 0, 0), (-head_size, head_size / 2, 0), (-head_size, -head_size / 2, 0), color)
triangle1.setPos(velocity_length, 0, 0)
# Draw the second triangle
triangle2 = Geometry.draw_triangle(
parent, (0, 0, 0), (-head_size, 0, head_size / 2), (-head_size, 0, -head_size / 2), color)
triangle2.setPos(velocity_length, 0, 0)
else:
# Draw the first triangle
triangle1 = Geometry.draw_triangle(
parent, (0, 0, 0), (-velocity_length, head_size / 2, 0), (-velocity_length, -head_size / 2, 0), color)
triangle1.setPos(velocity_length, 0, 0)
# Draw the second triangle
triangle2 = Geometry.draw_triangle(
parent, (0, 0, 0), (-velocity_length, 0, head_size / 2), (-velocity_length, 0, -head_size / 2), color)
triangle2.setPos(velocity_length, 0, 0)次は、src/planet.pyを開いて、惑星の速度ベクトルを描画できるようにします。self.velocity_lengthは、速度ベクトルの長さを表し、第1章の考察に従って、公転半径に比例、公転周期に反比例する値にしています。係数の0.5は、シミュレーター上で速度ベクトルを見えやすくするために設定した任意の値です。
class Planet:
def __init__(self, base, planet_dict):
self.base = base
# 中略
# 初期化メソッドの最後に、惑星の速度ベクトルを描画する
self.velocity_length = self.orbit_radius * 0.5 / self.orbit_period
self.planet_velocity_node = self.base.solar_system_node.attachNewNode(PandaNode(f'{self.name}_line'))
Geometry.draw_velocity_arrow(self.planet_velocity_node, self.velocity_length, planet_dict['color'])最後に、シミュレーターの実行ファイルであるdraw_planets_moving_constant.pyを修正して、速度ベクトルが惑星の進行方向を向くように回転させます。
class App(ShowBase, Window, Camera, Geometry, MakePlanets):
def __init__(self):
ShowBase.__init__(self)
Window.__init__(self)
Camera.__init__(self)
Geometry.__init__(self)
MakePlanets.__init__(self, PLANET_DICT_LIST)
self.count = 0
self.referenced_planet_name = 'Earth' # (1)
self.taskMgr.doMethodLater(0.1, self.update_planets, 'update_planets')
def update_planets(self, task):
for name, planet in self.planet_instance_dict.items():
if name != 'Sun':
diff_heading = BASE_ROTATE_SPEED * self.count / planet.orbit_period
heading = planet.initial_heading + diff_heading
position = Point3(*convert_to_cartesian(planet.orbit_radius, 90, heading))
planet.planet_model_node.setPos(position)
planet.pre_position = planet.position
planet.position = position
# planet.planet_line_node.setH(heading) # 公転角度を示す線を見えなくする # (2)
# 速度ベクトルの描画
planet.planet_velocity_node.setPos(position) # ここから(3)
planet.planet_velocity_node.setH(heading + 90) # ここまで(3)
if diff_heading <= 400:
self.draw_orbit(planet)
if name == 'Mercury':
self.update_top_left_text()
planet.update()
self.count += self.speed
return task.again上記コードは、地球と火星に速度ベクトルを表示できるようにする改造箇所を示しています。コメント番号部分を解説します。
(1)のself.referenced_planet_name は、カメラの視点を追従させる基準の惑星を指定しています。'Earth' を設定することで、カメラが常に地球を中心に追いかけるようになります。
(2)の1行をコメントアウトすることで、惑星の公転角度を表す線を見えなくしています。この線は今回のシミュレータでは不要だからです。
(3)の2行を追記します。planet.planet_velocity_nodeは速度ベクトルが描画されたノードです。setPosで位置を惑星モデルの中心に、setHで角度を惑星の進行方向に回転させます。
以上で、改造は完了しました。シミュレータを実行してみましょう。
2.2 地動説アニメーションを実行する
改造したシミュレータを実行するには、コマンドライン(PowerShellやターミナル)に次のコマンドを入力して実行します。
$ cd ~/Documents/solar_system
$ python draw_planets_moving_constant.py実行結果
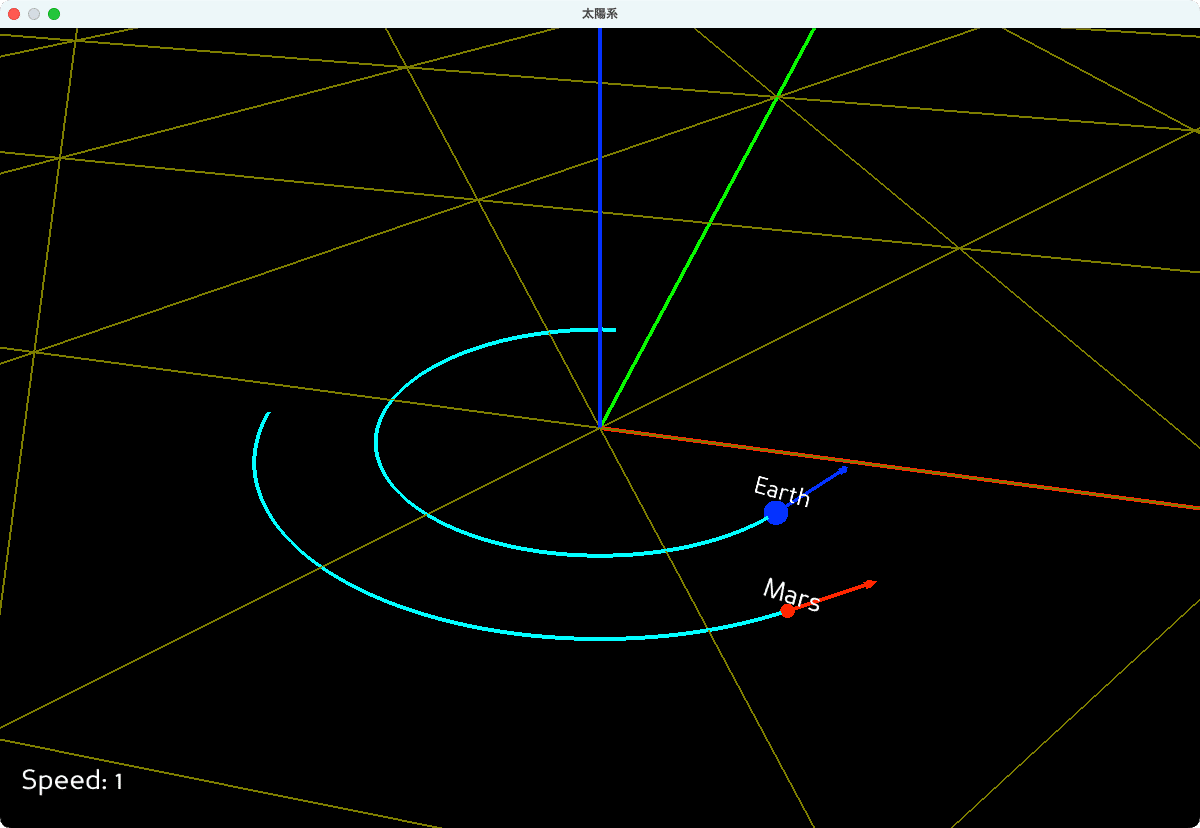
図1は、改造した太陽系シミュレーターの実行結果です。地球(Earth)と火星(Mars)のみを表示し、各惑星に速度ベクトルを追加しました。この速度ベクトルにより、その瞬間の惑星の進行方向が一目でわかります。地動説においては、速度ベクトルの方向は公転円に対して接線方向になります。
2.3 この章のまとめ
地動説に基づく太陽系シミュレーターを改造し、地球と火星の進行方向をベクトルとして表示しました。次の章では、地球を固定した場合の火星の動きをシミュレートします。
第3章:天動説による火星の逆行の視覚化
火星の逆行現象を地球からの視点で正確に表現するために、まずベクトルの合成について説明します。地球から見た火星の動きは、火星の速度ベクトルから地球の速度ベクトルを引いた、すなわち速度ベクトルの差によって得られる合成ベクトルで表されます。
3.1 ベクトルの合成と相対速度
ベクトルの合成とは
ベクトルの合成は、複数のベクトルを足し合わせて一つのベクトルを得る操作です。物理学では、異なる座標系や基準点から見た運動を統一的に扱うために重要です。
地球から見た火星の相対速度

地球と火星はそれぞれ独自の速度ベクトルを持っています(図2)。地球から見た火星の相対速度ベクトルは、次のように計算されます。

$$
v_{相対}=v_{火星}−v_{地球}
$$
$${v_{火星}:火星の速度ベクトル(赤)}$$
$${v_{地球}:地球の速度ベクトル(青)}$$
$${v_{相対}:地球から見た火星の相対速度ベクトル(緑)}$$
図3の相対速度ベクトル(緑)は、地球を基準としたときに火星がどのように動いているかを示します。
3.2 地球中心の座標系への変換
座標系の変更
これまでのシミュレーションでは、太陽を中心とした地動説の座標系を使用していました。ここでは、地球を固定し、火星の動きを相対的に表現するために、地球中心の座標系に変換します。
座標変換の方法
地球の位置ベクトルを計算する。
火星の位置ベクトルから地球の位置ベクトルを減算し、火星の相対位置を求める。
$$
r_{相対}=r_{火星}−r_{地球}
$$
$${r_{火星}:火星の位置ベクトル}$$
$${r_{地球}:地球の位置ベクトル}$$
$${r_{相対}:地球から見た火星の相対位置ベクトル}$$
3.3 天動説アニメーションの実装
第2章までで実装したプログラムを改造し、天動説のアニメーションを実装します。修正するファイルは draw_planets_moving_constant.py のみです。以下に修正箇所のコードを示し、コメント番号部分を詳しく解説します。
class App(ShowBase, Window, Camera, Geometry, MakePlanets):
def __init__(self):
ShowBase.__init__(self)
Window.__init__(self)
Camera.__init__(self)
Geometry.__init__(self)
MakePlanets.__init__(self, PLANET_DICT_LIST)
self.count = 0
self.referenced_planet_name = 'Earth'
self.relative_vector_node = None # (2)
self.taskMgr.doMethodLater(0.1, self.update_planets, 'update_planets')
def update_planets(self, task):
# 地球の位置を計算する
earth = self.planet_instance_dict['Earth'] # ここから(3)
earth_diff_heading = BASE_ROTATE_SPEED * self.count / earth.orbit_period
earth_heading = earth.initial_heading + earth_diff_heading
earth_position = Point3(*convert_to_cartesian(earth.orbit_radius, 90, earth_heading)) # ここまで(3)
for name, planet in self.planet_instance_dict.items():
if name != 'Sun':
diff_heading = BASE_ROTATE_SPEED * self.count / planet.orbit_period
heading = planet.initial_heading + diff_heading
position = Point3(*convert_to_cartesian(planet.orbit_radius, 90, heading)) - earth_position # (4)
planet.planet_model_node.setPos(position)
planet.pre_position = planet.position
planet.position = position
# planet.planet_line_node.setH(heading) # 公転角度を示す線を見えなくする
# # 速度ベクトルの描画
# planet.planet_velocity_node.setPos(position) # ここから(5)
# planet.planet_velocity_node.setH(heading + 90) # ここまで(5)
# 地球から見た火星の相対速度ベクトルを表示
if planet.name == 'Mars': # ここから(6)
planet.planet_velocity_node.setPos(position)
planet.planet_velocity_node.setH(heading + 90)
velocity_end_position = Point3(*convert_to_cartesian(planet.velocity_length, 90, heading + 90))
earht_velocity_node_position = position + velocity_end_position
earth.planet_velocity_node.setPos(earht_velocity_node_position)
earth.planet_velocity_node.setH(earth_heading + 270)
# ノードを削除し、参照をリセットする
if self.relative_vector_node is not None: # (8)
# if self.relative_vector_node is not None and self.count % 20 != 0:
self.relative_vector_node.removeNode()
self.relative_vector_node = None
relative_vector = Point3(*convert_to_cartesian(planet.velocity_length, 90, heading + 90)) + \
Point3(*convert_to_cartesian(earth.velocity_length, 90, earth_heading + 270))
radus, _, phi = convert_to_polar(relative_vector)
self.relative_vector_node = self.render.attachNewNode(PandaNode('relative_vector'))
Geometry.draw_velocity_arrow(self.relative_vector_node, radus, (0, 1, 0))
self.relative_vector_node.setPos(position)
self.relative_vector_node.setH(phi) # ここまで(6)
# if diff_heading <= 400: # (7)
if True:
self.draw_orbit(planet)上記コードは、天動説アニメーションとして、地球中心で火星の動きを視覚化します。「地球から見た火星の相対速度ベクトル」は $${v_{相対}=v_{火星}−v_{地球}}$$ のベクトル計算から求められます。コードのコメント番号部分を解説します。
(1)で必要なPanda3Dの機能をインポートします。Point3は、3次元空間の位置を表すクラスで、x, y, z の座標を保持します。PandaNodeは、Panda3Dのシーングラフを構成する基本ノードで、新しいシーン要素を作成する際に使用します。
(2)は、「地球から見た火星の相対速度ベクトル」を描画するためのノード(self.relative_vector_node)を初期化しています。
(3)は、地球の位置情報(地動説における)を計算しています。 そして、(4)で、惑星の位置情報を計算する際に、地球の位置を減算することで、地球を原点とした座標系(天動説)に変換します。
(5)の2行をコメントアウトし、(6)のコードに書き換えることで、「地球から見た火星の相対速度ベクトル」を計算し、正しい位置に配置しています。self.relative_vector_node.removeNode() によって古いベクトルを削除し、新しいベクトルを生成・描画することで、最新の相対速度ベクトルを常に表示できます。
最後に、(7)の条件式を「if True:」に書き換えます。これで、角度の制限なく惑星の軌跡を描くことができます。
以上で改造は完了しました。シミュレーションを実行しましょう。プログラムを実行するには、次のコマンドを実行します。
$ python draw_planets_moving_constant.py3.4 火星の逆行現象の視覚的確認

図4は天動説における火星の運行をアニメーションで表現したものです。火星には3本のベクトルが表示されています。これらベクトルは次の速度ベクトルを表します。
$${v_{火星}:火星の速度ベクトル(赤)}$$
$${v_{地球}:地球の速度ベクトル(青)}$$
$${v_{相対}:地球から見た火星の相対速度ベクトル(緑)}$$
アニメーションを実行すると、以下の現象が観察できます。
地球が火星を追い抜く際:
相対速度ベクトル(合成ベクトル)が一時的に逆向きになります。
火星が地球から見て逆方向に動いているように見えます。
3.5 地球から見た火星の相対速度ベクトルの変化を検証する
上記コードの(8)の条件式を書き換えることで、火星の相対速度ベクトルを軌跡上に保持しておくことが可能になります。これで、火星の相対速度ベクトルの時間的変化を検証できます。
# ノードを削除し、参照をリセットする
# if self.mars_velocity_from_earth_node is not None: # コメントにする
if self.mars_velocity_from_earth_node is not None and self.count % 20 != 0:
上記修正後、シミュレーターを実行することで、図5の画像が得られます。この図は、20ステップごとに「地球から見た火星の相対速度ベクトル」を軌跡上に残すことで、相対速度ベクトルの変化を視覚化しています。
火星の逆行が起きるときに、徐々に速度が遅くなり、追い抜く瞬間に最短になります。そして、逆行が終わると速度が速くなっていることが確認できました(図5)。
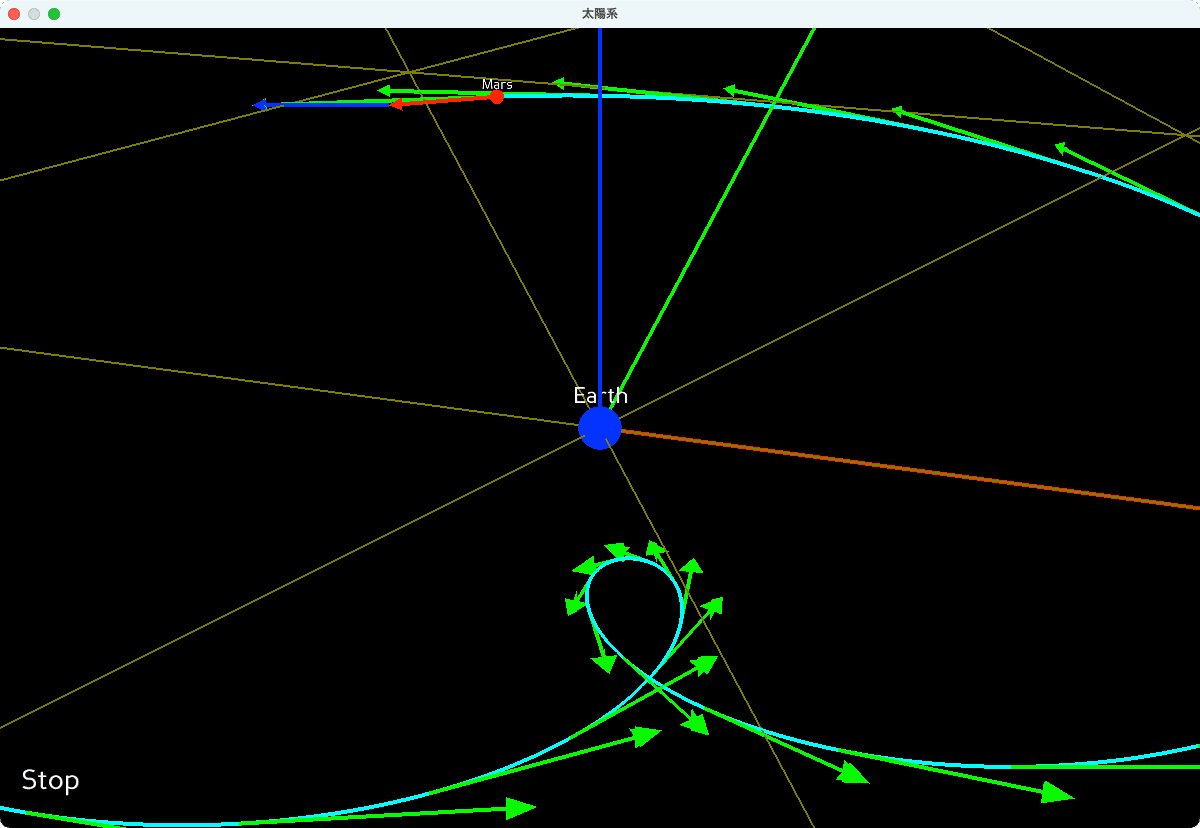
相対速度が最大になるのは、地球と火星が太陽を挟んで、最も離れた瞬間です(図6)。つまり、地球と火星が逆方向に動く時に、相対速度ベクトルが最大になるということです。これで、相対速度の変化の検証を終わります。
3.6 この章のまとめ
ベクトルの合成を用いて、地球から見た火星の相対的な動きを表現しました。
地球中心の座標系に変換することで、火星の逆行現象をシミュレーションしました。
アニメーションによって、火星の逆行現象が地球と火星の速度ベクトルの合成によって生じることを視覚的に示しました。
第4章:火星から見た地球の運行
上記コードを改造することで、火星から見た地球の運行を再現できます。つまり火星人がいるとして、火星の天文学者が地球を観測すると、どういった結果が得られるかという問題です。
火星から見て地球はどういった軌跡を描くか、想像してから記事の続きを読んでください。
4.1 火星中心の天動説アニメーションを実装
draw_planets_moving_constant.pyを修正します。修正済みのコードを次に示します。
class App(ShowBase, Window, Camera, Geometry, MakePlanets):
def __init__(self):
ShowBase.__init__(self)
Window.__init__(self)
Camera.__init__(self)
Geometry.__init__(self)
MakePlanets.__init__(self, PLANET_DICT_LIST)
self.count = 0
self.referenced_planet_name = 'Mars'
self.relative_vector_node = None
self.taskMgr.doMethodLater(0.1, self.update_planets, 'update_planets')
def update_planets(self, task):
# 火星の位置を計算する
mars = self.planet_instance_dict['Mars']
mars_diff_heading = BASE_ROTATE_SPEED * self.count / mars.orbit_period
mars_heading = mars.initial_heading + mars_diff_heading
mars_position = Point3(*convert_to_cartesian(mars.orbit_radius, 90, mars_heading)) # ここまで(3)
for name, planet in self.planet_instance_dict.items():
if name != 'Sun':
diff_heading = BASE_ROTATE_SPEED * self.count / planet.orbit_period
heading = planet.initial_heading + diff_heading
position = Point3(*convert_to_cartesian(planet.orbit_radius, 90, heading)) - mars_position # (4)
planet.planet_model_node.setPos(position)
planet.pre_position = planet.position
planet.position = position
# planet.planet_line_node.setH(heading) # 公転角度を示す線を見えなくする
# # 速度ベクトルの描画
# planet.planet_velocity_node.setPos(position)
# planet.planet_velocity_node.setH(heading + 90)
# 火星から見た地球の速度ベクトルを表示
if planet.name == 'Earth':
planet.planet_velocity_node.setPos(position)
planet.planet_velocity_node.setH(heading + 90)
velocity_end_position = Point3(*convert_to_cartesian(planet.velocity_length, 90, heading + 90))
earht_velocity_node_position = position + velocity_end_position
mars.planet_velocity_node.setPos(earht_velocity_node_position)
mars.planet_velocity_node.setH(mars_heading + 270)
# ノードを削除し、参照をリセットする
if self.relative_vector_node is not None:
# if self.relative_vector_node is not None and self.count % 20 != 0:
self.relative_vector_node.removeNode()
self.relative_vector_node = None
relative_vector = Point3(*convert_to_cartesian(planet.velocity_length, 90, heading + 90)) + \
Point3(*convert_to_cartesian(mars.velocity_length, 90, mars_heading + 270))
radus, _, phi = convert_to_polar(relative_vector)
self.relative_vector_node = self.render.attachNewNode(PandaNode('relative_vector'))
Geometry.draw_velocity_arrow(self.relative_vector_node, radus, (0, 1, 0))
self.relative_vector_node.setPos(position)
self.relative_vector_node.setH(phi) 上記コードは、火星から見た地球の運行をシミュレートします。「earth」の文字列を「mars」に、「Earth」の文字列を「Mars」に、「Mars」の文字列を「Earth」に置換しています。コードの説明は、第3章のコードと同じなので省略します。
上記コードを実行すると、火星中心の天動説がシミュレートできます。

図7の結果から、火星から地球を見た場合でも、地球が火星を追い抜く際に逆行が生じることがわかりました。つまり、火星の天文学者も「地球の逆行」の謎を解く過程で、地動説に到達する可能性があることが考察されました。
4.2 この章のまとめ
火星を中心にした天動説を実装して、地球の運行を再現しました。地球が火星を追い抜くときに、惑星の逆行現象が生じることが確認できました。第3章の「地球から見た火星の軌跡」と第4章の「火星から見た地球の軌跡」は、原点に対して互いに鏡像関係になっています。
観測者と観測対象は、互いに相手を見ると常に逆方向に動いているように見えます。つまり、空間上の運動は絶対的なものではなく、相対的なものであるという結論に至ります。
第5章:まとめと考察
5.1 学んだことの整理
本記事では、地球と火星の公転運動を数学的に解析し、3Dアニメーションを用いてその動きを視覚的に再現しました。以下に主要な学びをまとめます。
地動説と天動説での火星の動きの違い:地動説では、太陽を中心に地球と火星がそれぞれの軌道を公転し、その公転速度の差によって火星の逆行現象が生じることを確認しました。一方、天動説では地球を中心とした座標系に変換し、火星の動きを相対的に捉えることで、逆行現象を説明しました。
ベクトルを用いた逆行現象の理解:速度ベクトルの合成を用いて、地球から見た火星の相対的な動きを表現しました。特に、地球の進行方向の逆向きベクトルと火星の進行方向ベクトルを合成することで、火星の逆行が生じるメカニズムを理解しました。
5.2 他の天体や現象への応用
他の天体や現象への応用可能性:今回のシミュレーション手法は、他の惑星や衛星、小惑星の運動解析にも応用できます。第4章では、火星から見た地球の運行を再現することで、惑星の逆行が地球以外の天体でも生じることを証明できました。
5.3 結論
漫画・アニメ『チ。』で取り上げられた火星の逆行現象を、数学的な解析と3Dアニメーションを通じて視覚的に解決しました。「惑星の逆行」という謎めいた現象が、公転速度の差と速度ベクトルの合成によって説明できることが分かりました。このように、不思議な現象を解明していくプロセスは、科学の醍醐味と言えるでしょう。
この記事が、惑星の逆行現象の理解の深まりにつながるならば幸いです。
