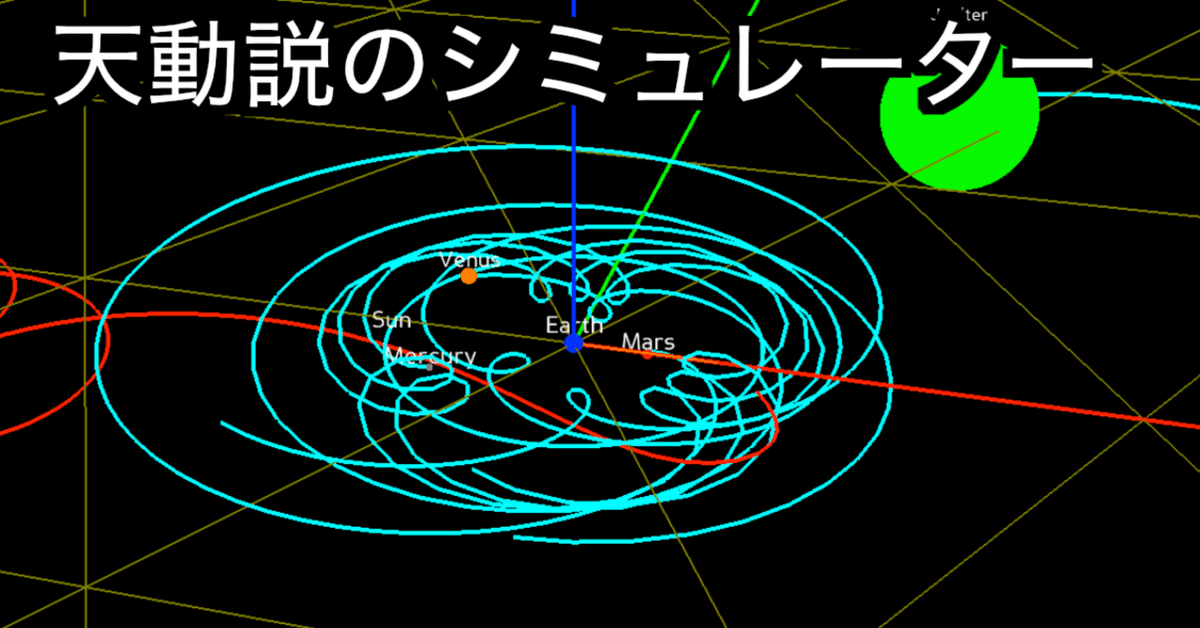
Python Panda3Dライブラリで天動説の惑星の動きを再現する

2024年11月4日 18:56

この記事は著者が作成したものです。日経ソフトウエア様のご承諾をいただき、著者の責任において作成・公開しています。

本記事では、実際の天体データを基にして、地球を中心に惑星が運行する「天動説」のシミュレーションをPythonで再現します。漫画／アニメ「チ。」でも描かれているように、古代の天文学者たちは、地球を宇宙の中心とする天動説を提唱していました。彼らが目にしていた火星の逆行などの複雑な動きも、このシミュレーションで再現可能です。

図1に示すように、天動説における火星の軌道は単純な円運動ではなく、地球から見た火星の位置があたかも行ったり来たりするように見えます。この現象は、天動説を唱える人々にとっても謎であり、その理由を説明するために、複雑な円運動（エピサイクル）を考案していました。この複雑な円運動を3Dアニメーションで再現することが、本記事の目標です。

元となる雑誌記事の紹介

日経ソフトウエア2024年3月号の特集記事として、「太陽系シミュレーター」の作り方を解説しました。この特集記事の完成形から、一部のファイルを修正するだけで、簡単に「天動説の太陽系」を再現できます。この記事の内容を実際に試してみたい方は、次に紹介する雑誌をお買い求めください。

↓↓↓特集3 Pythonで「太陽系シミュレーター」を作る↓↓↓

この雑誌記事は、次のムックにも収録されています。
↓↓↓第9章　 Pythonで「太陽系シミュレーター」を作る↓↓↓

第1章：地動説の太陽系を再現する

初めに、「地動説」の太陽系を見てみましょう。修正前のプログラムを実行すると、次の画像が得られます。

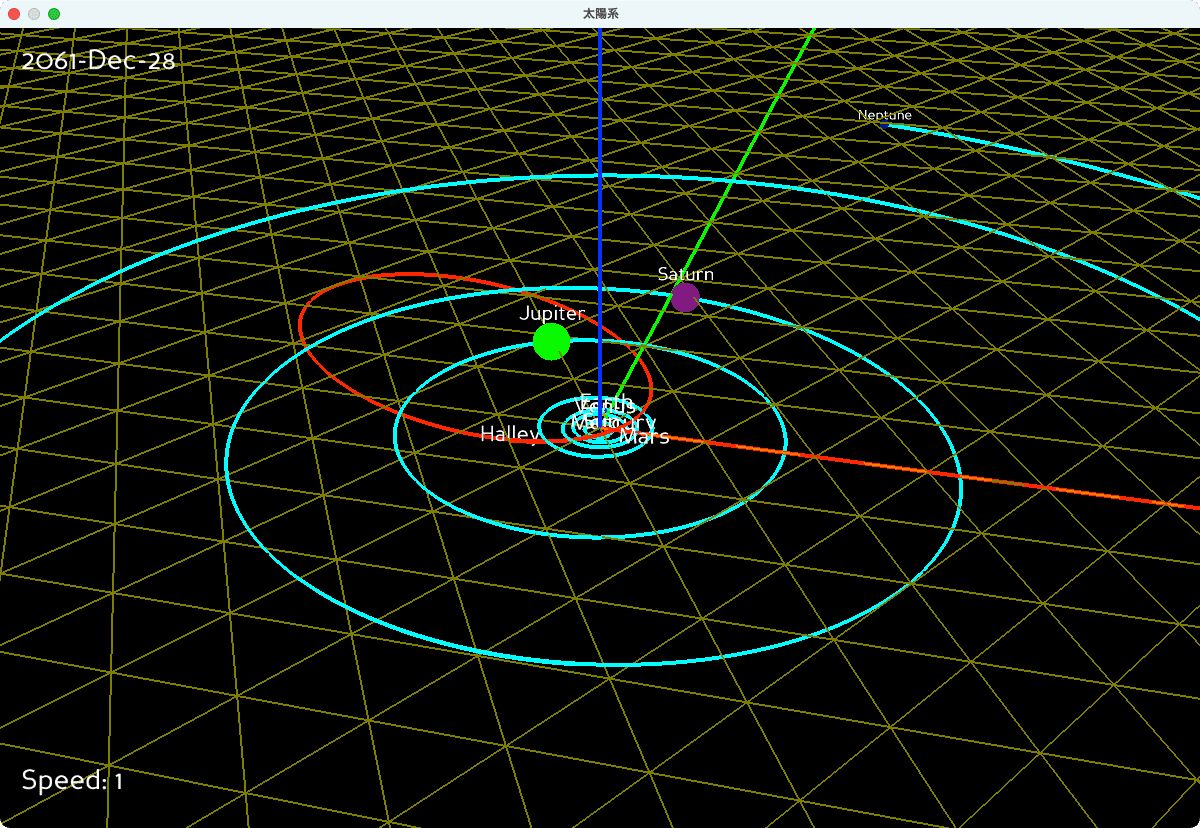
上記のプログラムは、日経ソフトウエア特集記事に掲載されています（図2、図3）。この雑誌記事では、「ハレー彗星」の軌跡（赤線）を惑星の動きと同時に確認できます。このプログラムは、小規模の改造で他の天文イベントを再現できるように設計されています。

ここでは応用例の一つとして、天動説の太陽系を再現します。修正するファイルは、horizons_api.pyとcamera.py、draw_planets_with_horizons_api.pyの3つを修正するだけです。まずは、horizons_api.pyの方から改造を始めます。

1.1 地動説の太陽系

ここからの作業を進めるには、地動説に基づく太陽系シミュレーターが完成していることが前提となります。まだシミュレーターが未完成の方は、特集記事を参考に、まずそちらを仕上げてください。

では、改造を開始しましょう。

1.2 Horizons Systemから地球基準の惑星位置情報を取得

srcフォルダーの中にあるhorizons_api.pyをテキストエディターで開いてください。このファイルは、NASAのHorizons Systemから惑星の正確な位置情報を取得して、惑星名をキーとする辞書として返却します。次のコードは、改造箇所を示したものです。

# horizons_api.pyの16、17行目

    # if name != 'Sun':
    #   obj = Horizons(id=horizons_id, location='@sun',
    if name != 'Earth':  # （1）
      obj = Horizons(id=horizons_id, location='@399',  # （2）
                     epochs={'start': start, 'stop': stop, 'step': step})

horizons_api.pyの16、17行目を書き換えます。（1）は、惑星名Earthのときは、位置情報の取得を行わないための条件式です。（2）は、location引数として、「@399」を指定します。この値は、「地球-月系重心（Earth-Moon Barycenter）」を基準点とすることを意味します。以上の改造で、地球以外の惑星と位置を、地球を基準として取得できるようになりました。

1.3 カメラの基準惑星を修正

次は、srcファルダーにあるcamera.pyを修正します。

# camera.pyの13行目

    # self.referenced_planet_name = 'Sun'
    self.referenced_planet_name = 'Earth'

camera.pyの13行目で、インスタンス変数referenced_planet_nameを「Earth」に変更します。referenced_planet_nameは、カメラの基準となる惑星名を表し、この惑星に固定した視点（カメラ）から惑星の運行を確認するために使用します。

1.4 起動ファイルを修正

最後に、起動ファイルdraw_planes_with_horizons_api.pyを修正します。

# draw_planes_with_horizons_api.pyの4行目

table_name = 'HALLEY'  # （1）

# draw_planes_with_horizons_api.pyの42行目

          # if planet.advanced_angle <= 400 or name in ['Hayabusa2', 'Halley']:
          if True:  # （2）

コードの4行目で、table_name = 'HALLEY'が定義されていることを確認します。（1）により、ハレー彗星の公転周期である76年間分のデータが7日おきに取得できます。具体的には、前回接近時の「1986-01-01」から次回接近時の「2062-01-01」までの惑星の位置情報がデータベースに保存されます。

最後に、コードの42行目の条件式を「if True:」に書き換えます。（2）により、すべての惑星の軌跡を角度の制限なく描画できるようになります。以上で、改造は終了です。

1.5 古いデータベースの削除

このシミュレーターは、Horizons Systemからの情報の取得を初回起動時のみ実行するように設計されています。そのため、dataフォルダー内に、「horizons_api.sqlite3」ファイルが存在すると、天動説のデータを取得できません。

したがって、dataフォルダー内にデータベースファイルが保存されていたら、削除してください。これですべての準備が完了しました。

1.6 天動説シミュレーターの起動

プログラムを実行してみましょう。コンソール（PowerShellやターミナルなど）を開いて、次のコマンドを実行してください。初回起動時は、天体情報の取得と保存に時間がかかりますので、そのままお待ちください（環境にもよりますが、数十秒から数分かかります）。2回目以降は、すぐにシミュレーターが起動して、次に示すシーンが得られます。

cd ~/Documents/solar_system
python draw_planets_with_horizons_api.py

1.7 天動説のシミュレーション

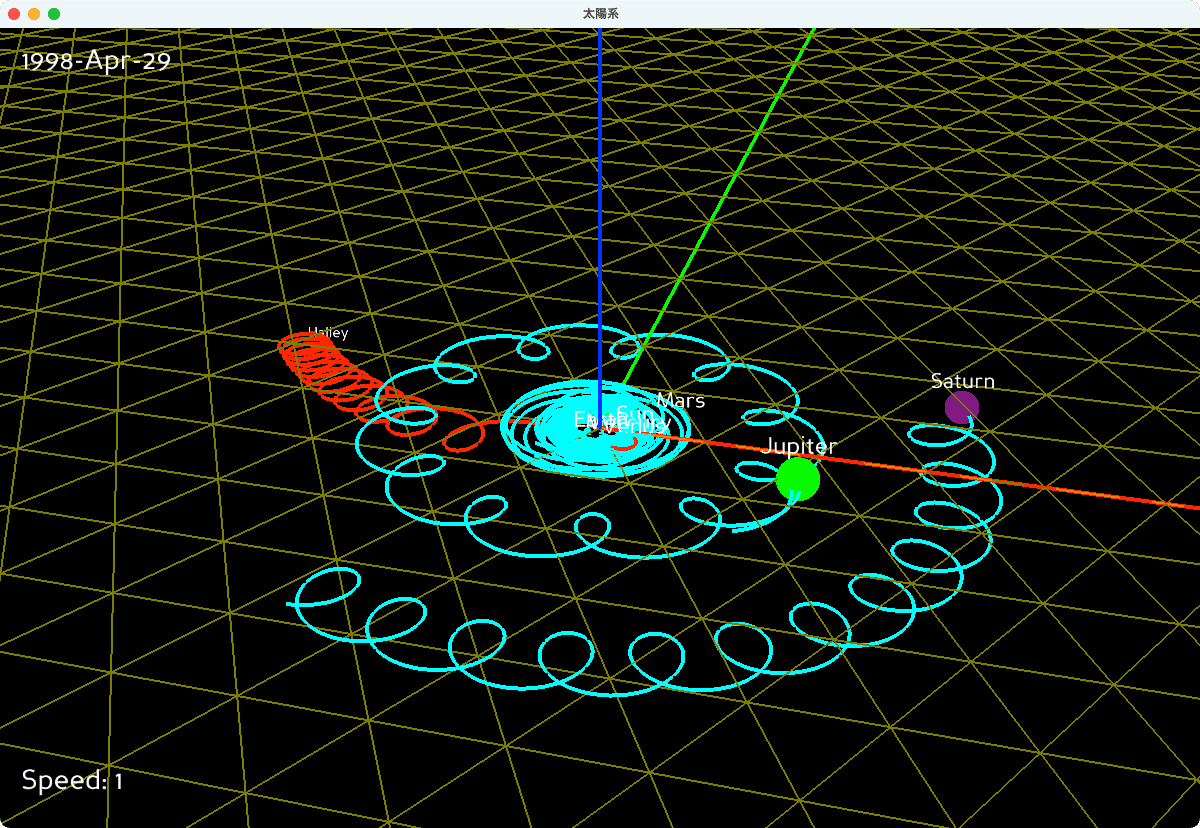
図4、図5は、天動説の惑星の軌跡を描いたシミュレーション結果です。複雑な円運動（エピサイクル）が、惑星の正確な位置情報から再現できました。図2、図3と見比べると、その複雑さが一目瞭然です。

1.8 火星の軌跡を確認する

火星の軌跡のみを描画してみましょう。起動ファイルdraw_planes_with_horizons_api.pyをさらに1行修正します。


# draw_planes_with_horizons_api.pyの42行目

          # if planet.advanced_angle <= 400 or name in ['Hayabusa2', 'Halley']:
          # if True:
          if name in ['Mars']:  # （1）

draw_planes_with_horizons_api.pyの42行目は、惑星の軌跡を描く条件を定義しています。この1行を（1）のように、火星（Mars）のみ描画する条件式に変更します。

上記の変更後にプログラムを実行すると、次のアニメーションが描画されます。左上の日付の火星の正確な位置情報から複雑な円運動が再現できました。

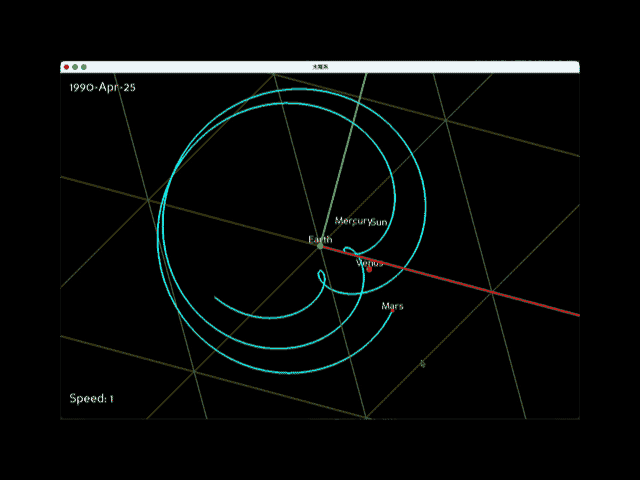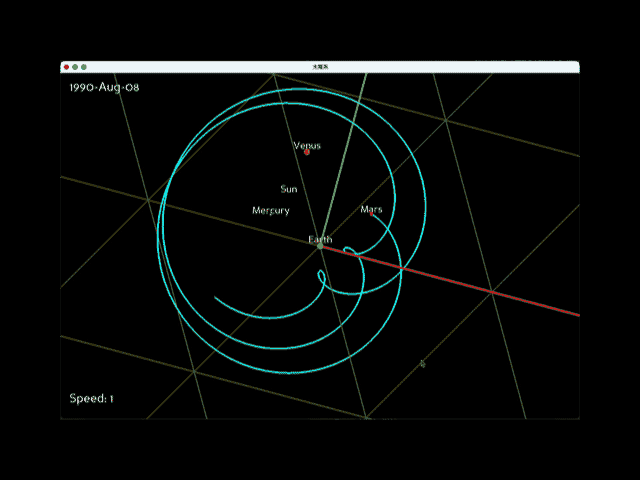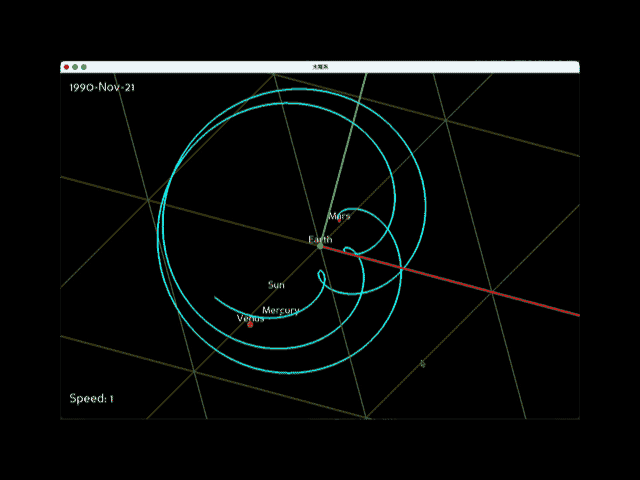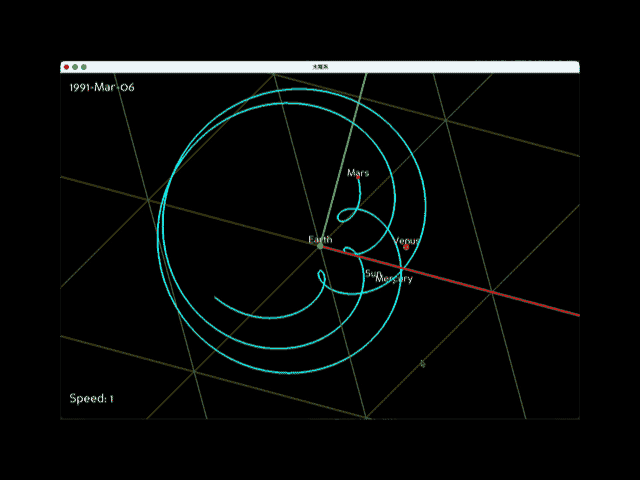
地球はほぼ円形の公転軌道を持つのに対し、火星は楕円形の公転軌道を描きます。つまり、火星の公転速度は一定ではありません。そのため、地球が火星を追い越す際に描かれる小さな円（周転円）の大きさが異なる点にご注意ください。火星の速度が速いときには小さな円を、遅いときには大きな円を描くことになります。

以上で、天動説の太陽系シミュレーターは完成です。

第2章：オッカムの剃刀

科学において、同じ事象を説明するのに、より簡単な説明を優先する考え方は「オッカムの剃刀」として知られています。これは、「必要以上に仮定を増やさない」という原則で、簡潔で無駄のない説明が優れているとする考え方です。この原則を適用することで、複雑な説明よりもシンプルな説明が望ましいとされ、科学的探求の指針のひとつとなっています。

天動説と地動説を例に考えてみましょう。

天動説
天動説では、地球が宇宙の中心に固定され、すべての惑星が地球を中心に回転していると説明されます。しかし、実際に観測される惑星の動き（特に火星の逆行運動）を説明するためには、各惑星が小さな円（周転円）を描きながら回転するという複雑な仕組みを仮定する必要がありました。これにより、エピサイクルや、さらなる補正のための仮定が次々と追加されていき、説明が非常に複雑になりました。

地動説
一方で、地動説は、地球と他の惑星が太陽を中心に回転していると仮定することで、惑星の運行を非常にシンプルに説明します。地動説によると、火星の逆行現象は、地球が火星を内側から追い越す際に生じる見かけの現象であり、エピサイクルのような複雑な補正は不要です。太陽を中心に置いたこのモデルは、天体の動きの説明が簡潔で理解しやすくなり、観測データともよく一致します。

2.1 オッカムの剃刀の適用

天動説と地動説のどちらが「オッカムの剃刀」に適しているかといえば、明らかに地動説が優位です。地動説は、仮定を減らしながらも観測事実を説明するシンプルなモデルであり、無駄な補正を必要としないため、オッカムの剃刀の原則に合致します。科学においては、このように仮定が少なく、簡潔な理論がより信頼される傾向にあります。

ただし、「オッカムの剃刀」が必ずしも正しいとは限りません。私たちは往々にして、シンプルで美しい説明に惹かれがちですが、それは必ずしも自然の真理に即しているとは限らないからです。実際、自然界には複雑な要因や非線形な現象が多く存在し、それらを単純に説明することが不可能な場合も少なくありません。

終わりに

太陽系シミュレーター（天動説）を楽しんでいただけましたでしょうか。中世の天文学者たちが悩んだ問題を、現代のコンピューターグラフィックスで再体験していただけたかと思います。さまざまな視点から宇宙を探求する楽しさを感じていただけたなら幸いです。

動画で太陽系シミュレーターを確認したい方は、YouTubeでご覧いただけます。

前の記事
[Pyxel]Pythonでマトリックスの世界を再現｜creativival (note.com)
次の記事
…

その他のタイトルはこちら