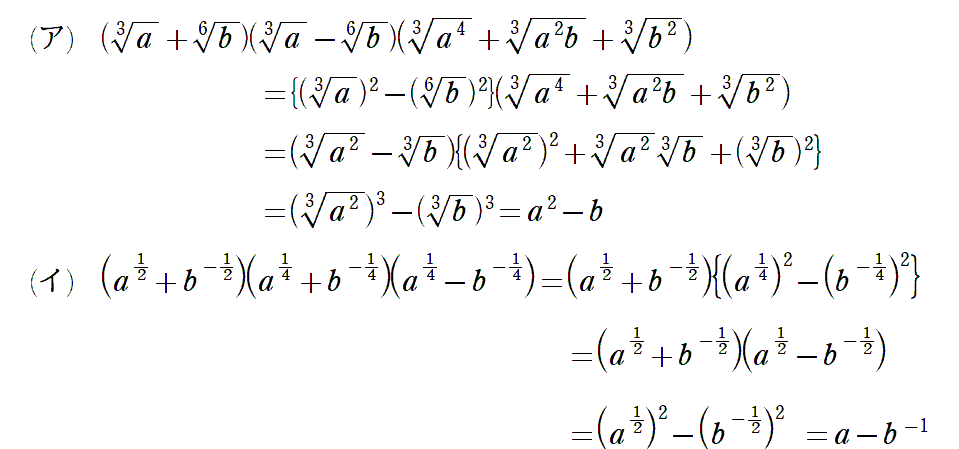【指数関数】 〈1〉 計算
指数関数と対数関数は、対になる学習内容です。どちらか感じが掴めたら、もう一方も同様に考えることができるはずです。計算、グラフ、方程式、最大最小など、問題の意図、形式なども似通っています。
さあ、克服への第一歩を踏み出していきましょう。
まずは、指数法則ですね。中学校の学習内容ですが、基本とは言え、かなりの難易度だと思っています。なんと言っても、ややこしい!
[Method] 指数法則

高校数学では、指数の拡張がされ、分数やマイナスの指数が登場してきます。法則は同じなのだけど、さらに、ややこしさも拡張されてしまいます!
[Method] 反応できるか?
2、4、8、16、32、64、128、256、512、1024
3、9、27、81、243
5、25、125、625
6、36、216
7、49、343 などと、その整数倍
このような数を見たときに、瞬間的に「n乗のグループ」と反応できるかで、スピード感が全く違ってきます。
さらには、例えば、
72であれば、36の2倍
96であれば、32の3倍
55だと???だけど、54だとチャンスあり!
とか、どんどん反応していけるようになれば、「センスあり」ってなっていくのです。
[Method] 指数の拡張

東北大学の総長をされ、LEDや光通信の基礎となる研究をされた西澤潤一先生が言っておられました、
「独創性とか独創的発想とかも、地道な基礎研究から生まれてくるもの」
やはり、基礎・基本こそが大切であり、この2つのMethodを習熟していくことが、次の段階への礎(いしずえ)となります。
対数関数の場合にも同様ですが、まずは、底を揃えることが入り口で、さらに、できるだけ2とか3とか、小さい素数になっていると計算が進み易いです。
[Method] 指数の計算
1)底を揃える
2)揃える底は、できるだけ小さな素数に
最後の答えは、結構簡単な式になることが多いです。答えのイメージを持ちながら解くことも大切です。
〈例題1〉 基本的な式の計算

基本的な計算ですが、かなりややこしいです。分数やマイナスの指数、分数、累乗根など、丁寧な変形に慣れていきましょう。
〈例題2〉

〈例題解答例2〉
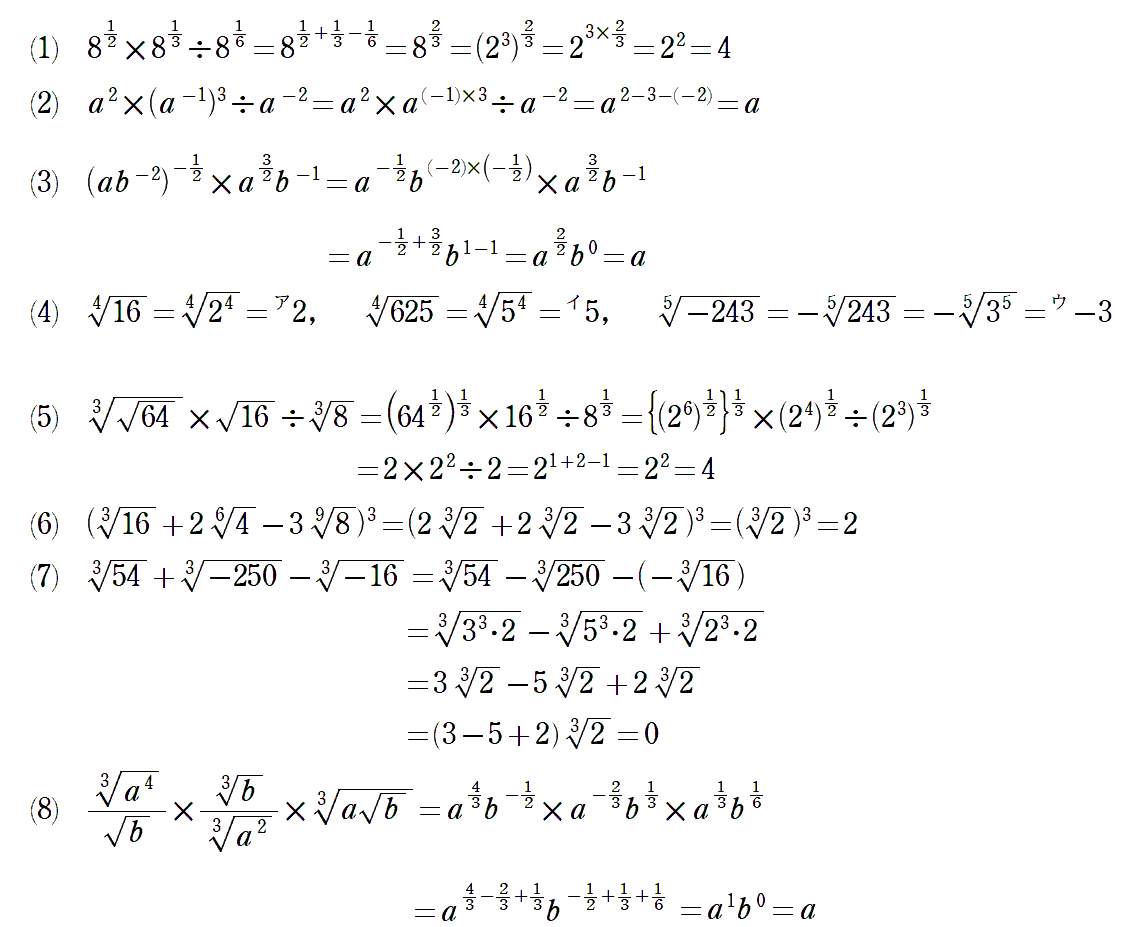
この種の問題は、問題集とかにたくさん掲載されているので、ミスなく解けるまで、習熟していきましょう。確かに数学は覚える科目ではありません。しかし、このような計算は、覚えてしまうほどに確実性を上げないと、計算の途中で自信を無くしてしまいます。
〈問題3〉

〈問題解答例3〉

〈問題4〉
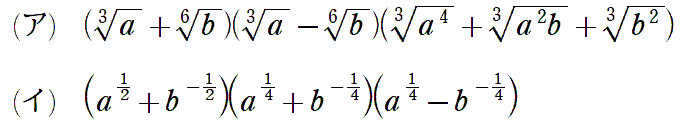
〈問題解答例4〉