
【微積分】 〈11〉 面積
図形によって、囲まれる部分の面積の求め方は様々です。「代数と幾何の一対一対応の美しさ」という観点から観ると、代数的な「関数」から、幾何的な「面積」が求まる「積分」は、まさにその典型です。
このシリーズでは、複雑な計算になりがちな「積分」について、スピードと確実性のアップを目指して解説します。
[Method] 求める領域(面積)をグラフで確認
・交点、上下など曲線の関係が大切なので、まずグラフを描画
・グラフを参考にし、上のグラフから下のグラフを引いて、適切な範囲で定積分を立式
〈例題1〉 :上下関係とx軸
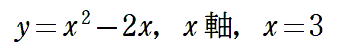

x軸に対して、上部にあるか下部にあるかで符号が変わってしまいます。きちんと確認する習慣をつけましょう。もちろん積分の範囲にも関わってきますからね。
〈例題解答例1〉

〈例題2〉 :上下関係と交点


放物線では、上下関係が明らかであることが多いのですが、モデルで構わないので、イメージを掴むようにしましょう。
〈例題解答例2〉

〈問題2〉
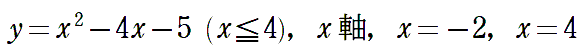
〈問題解答例2〉

〈問題3〉

〈問題解答例3〉

〈問題4〉

〈問題解答例4〉

〈問題5〉

〈問題解答例5〉

