
【指数関数】 〈2〉 グラフと大小関係
指数関数と対数関数は、対になる学習内容です。どちらか感じが掴めたら、もう一方も同様に考えることができるはずです。計算、グラフ、方程式、最大最小など、問題の意図、形式なども似通っています。
さあ、克服への第一歩を踏み出していきましょう。
まずは、底が3の例題を見ていきましょう。カーブの向きや位置をきちんと見極め、急激に増加していく様。減少していく様を目に焼き付けましょう。一般社会でも、「指数関数的に」という表現が使われるので、このタイミングでイメージをしっかり体得しましょう。
[Method] 指数関数のグラフ
・底が1より大きい → 単調増加
・底が0と1の間 → 単調減少
まずは、グラフの練習をするのだけど、きちんと描けなくても、だいたいのイメージが掴めれば大丈夫。細かい部分は、気にせずに。
大小関係は、グラフのイメージが掴めていることが大切なので、底を揃えていけば答えに近づける。
ただし、指数を揃えるパターンもあるので、その場合は底の大小関係によるので注意。
[Method] 大小関係
・底を揃える
・指数を揃える
〈例題1〉

〈例題解答例1〉



〈例題2〉 底を揃える+指数を揃える

〈例題解答例2〉

〈問題3〉
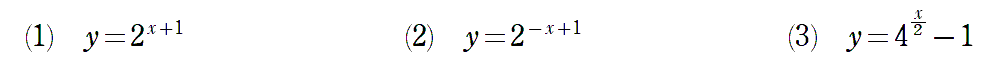
〈問題解答例3〉


〈問題4〉3数をそれぞれ〇乗する

〈問題解答例4〉

