【微積分】 〈１〉 微分の定義

　数学の歴史上、「三角比」「図形の性質」などは紀元前から使われていま
すが、「微積分」は、比較的最近の技法のようです。たいへんスマートで、体系的に確立されており、代数と幾何の一対一対応の美しさを味わうことのできる分野です。

---

[Method] 微分係数の定義

　微分係数：ｘ＝a における接線の傾き

微分の定義

x＝a、x=a+h の間の増加量について
変化の割合＝（xの増加量）／（yの増加量）
を考えます。
　変化の割合を見る両端の「差」hを 極限的に小さくして２点を近づけていくと、変化の割合が接線の傾きに近づいていきます。よって、上記　f＾(a)  をx=a における「微分係数」と呼びます。

[Method]   「微分係数」＝接線の傾き

---

単項式の加減＝代数的手法

　「微分の定義」式を用いた出題はそう多くないのですが、以下は、典型的な基本例題で、解法の中にこの問題特有のMethodが含まれています。それは、「微分の定義」式を（２つ）作り上げていく過程で、単項式の加減を利用します。これは、簡単に思いつくようなものではなく、入試対策として習熟してほしい解法なのですが、因数分解や極限など、他分野でも出てくる手法でもあります。

---

〈例題１〉

〈例題解答例１〉

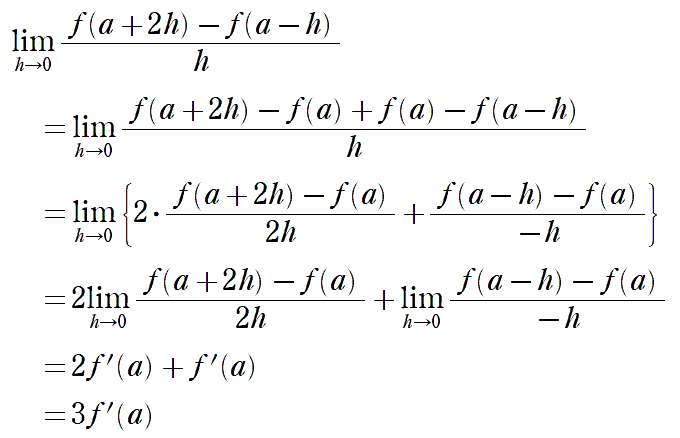
２行目のところで、f(a) を引いて足しています。これがMethodです！ ３行目以降にこれが活きてきて、「微分の定義」式が見えてきます。

いずれも、２ｈ、ーｈが変化の割合を見る両端の「差」にあたります。ですから、いずれもｆ’(a) になって、置き換えることができます。

式変形を工夫して、ｈの部分の様子を一致させることでｆ’(a) に置き換えていきます。

---

〈問題２〉

〈問題２〉

〈問題解答例２〉

---

〈問題３〉

〈問題３〉

〈問題解答例３〉