
【微積分】 〈2〉 接線(基本)
数学の歴史上、「三角比」「図形の性質」などは紀元前から使われていま
すが、「微積分」は、比較的最近の技法のようです。たいへんスマートで、体系的に確立されており、代数と幾何の一対一対応の美しさを味わうことのできる分野です。
[Method] 接線の方程式(微分係数=接線の傾き)
微分係数が接線の傾きであることから、直線の方程式を求めるMethodを
用いて、

この式は、大学入試問題に必ず出題されると断定できるほど、必須の立式です。さらに、この式でできた接線を用いて、以下の問いをこなしていくので、絶対に計算間違いは許されません。
1つの接点=1本の接線
滑らかな曲線では、曲線上の点=接点 において、x がただ一つ定まるので、接点における接線の傾き=微分係数を1つ求めることができる。よって、接線が1本だけ定まる。
微分係数、関数の値など代数的な計算が、図形的な接線と対応することは、シンプルに数学的で美しい。微積分は、このような対応の見事さをぜひ感じてほしいと思います。当たり前のようですがこういう場面で大局的なMethodとして、数学的なセンスが培われていくと考えます。

1つの接点=無数の接線
「滑らかな曲線」に対して、例えば、角のたった曲線、あるいは、半直線では、その角や端点で無数の接線を引くことができます。こういう点は、微分係数が一意に定まらないので、「微分可能ではない」と言っています。

[Method] 法線の方程式

公式としてはこうなるのですが、
垂直な直線の性質
m・m’=ー1
を使えば、傾きは求められるので、特段覚える必要はないと考えます。
[Method]
記憶で解くのではなくて、分野を超えた深い理解を意識して、公式を使っていきましょう。使うことで覚えていくので、覚える量を少なくすると、記憶の定着が早く正確になっていきます。
〈例題1〉

〈例題解答例1〉
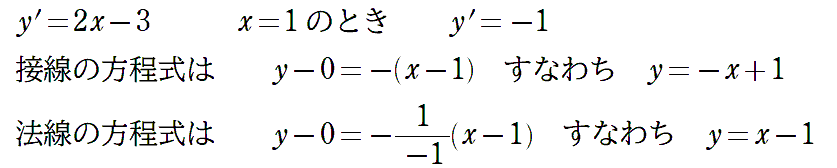
2次関数のグラフにおける接線の問題です。ただ求めるのではなくて、何を求めているのか。がとても大切です。グラフで整理しておきましょう。

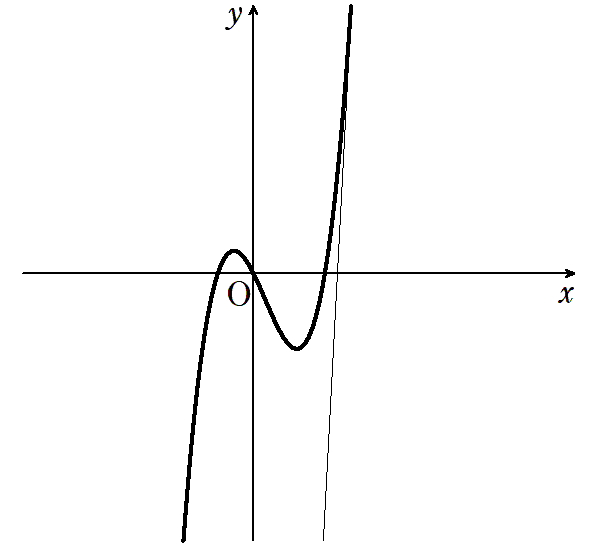
3次関数のグラフにおける接線の問題です。解法は全く同じですが、グラフで整理しておきましょう。
〈例題2〉

〈例題解答例2〉


〈問題3〉

〈問題解答例3〉

〈問題4〉

〈問題解答例4〉


