【微積分】 〈7〉 3次関数のグラフ
数学の歴史上、「三角比」「図形の性質」などは紀元前から使われていま
すが、「微積分」は、比較的最近の技法のようです。たいへんスマートで、体系的に確立されており、代数と幾何の一対一対応の美しさを味わうことのできる分野です。
[Method] 3次関数のグラフ
・3次の係数+極値の個数 →概形が確定
・最高次数(3次)の係数の正負 →大局的に増加、減少
まず、1次関数を考えてみよう。
1次の係数が正の場合は単調増加(直線)

1次の係数が負の場合は単調減少(直線)

3次関数でも同様に、3次の係数で増加・減少が決まります。
[Method]
奇数次数の関数のグラフは、最高次数の係数の正負によって、大局的な増加・減少が決まる。
例えば、3次の係数が負の場合、左上から右下へ、大きくは減少関数であり、一部分が増加するイメージを持つことが大切!
関数の増減については、最高次数の部分の値が一番大きな影響を及ぼすことは当然ですよね。
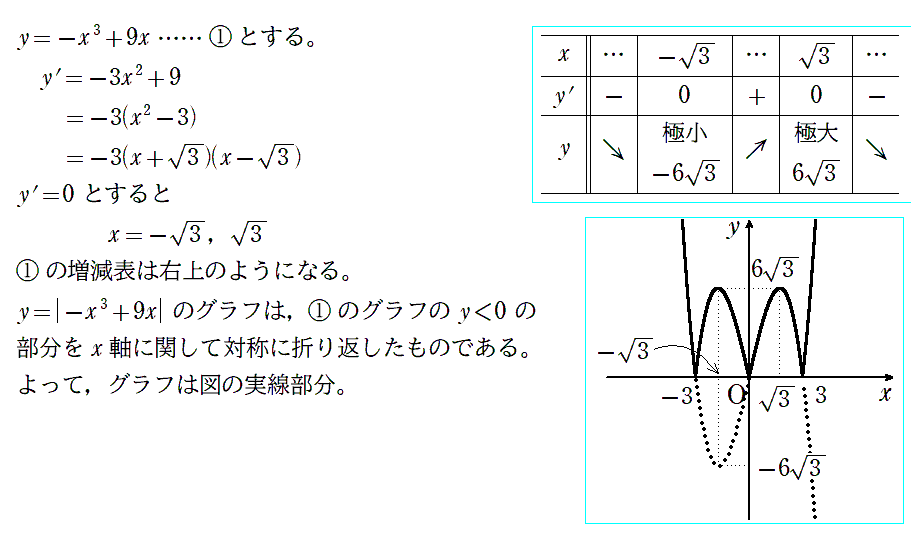
〈例題1〉

〈例題解答例1〉


この例題のグラフは、一部分の増加部分に着目して描くことになります。
しかし、同じグラフを縮尺を変え描くと、大局的には、大部分で減少していることがわかります。ほぼ、直線的に減少と言ってよいくらいです。

この事実を踏まえて、グラフを描くときには、両端が上下に突き抜けるように描くことを心がけましょう。
〈問題2〉
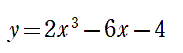
〈問題解答例2〉

〈問題3〉

〈問題解答例3〉


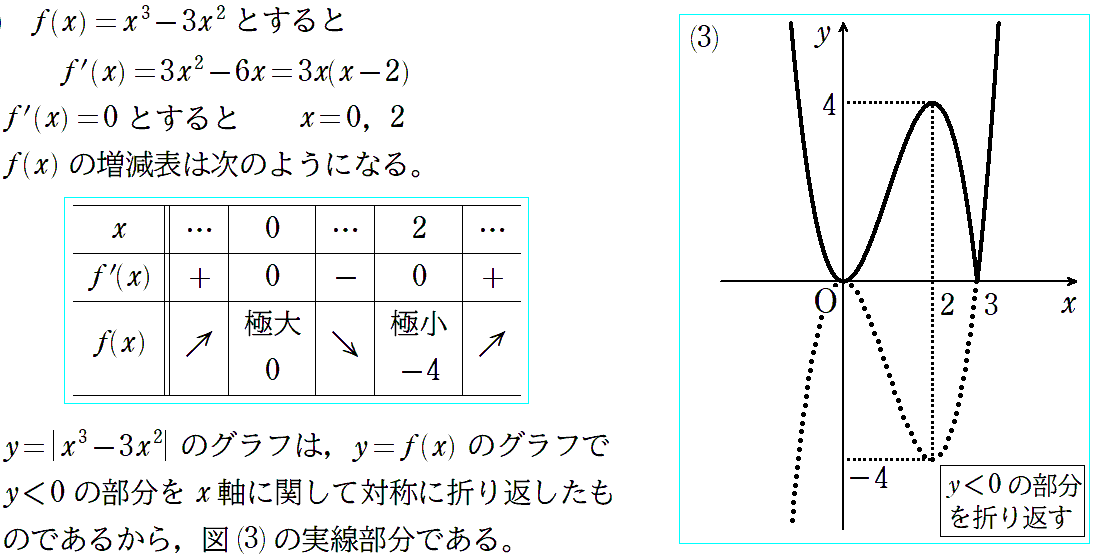
〈問題4〉
大外に絶対値がある場合は、普通に描いてから、負の部分をひっくり返します!

〈問題解答例4〉
〈問題5〉

〈問題解答例5〉