
【微積分】 〈9〉 変曲点
数学の歴史上、「三角比」「図形の性質」などは紀元前から使われていま
すが、「微積分」は、比較的最近の技法のようです。たいへんスマートで、体系的に確立されており、代数と幾何の一対一対応の美しさを味わうことのできる分野です。
〈例題1ー1〉

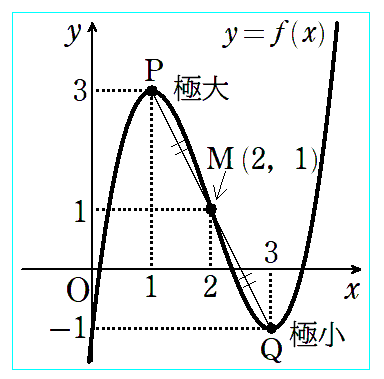
この3次関数のグラフは以下のようになります。このとき、Mが極大値と極小値の中点であり、点Pと点Qは点Mについて対称となります。
実は、グラフ全体も、点Mについて、点対称になっています。
[Method] (3次関数の変曲点)
・極大値と極小値の中点=「対称点」=「変曲点」
・変曲点では、グラフのカーブが右曲がりから左曲がりに変化
・変曲点では、接線は引けるが、交わっているようにしか見えない
自転車のハンドルに例えてお話をしましょう。
上のグラフが自転車道路だとすれば、左下から運転してきたとしましょう。わずかではありますが、上に上がりながら、ハンドルは右に切りつづけています。 少しずつ切角を大きくしていき、点Pで最大角になります。そして、点Mに差し掛かった時、一瞬、ハンドルが真正面を向きます。その後、今度は、ハンドルを左に切ることになります。
実は、
ハンドルの方向=接線の傾き
です。
〈例題1ー2〉

〈例題解答例1〉

今回のテーマ「変曲点」を、その名前こそ出していませんが、公式化したのが以下の例題です。「変曲点」の座標が係数で表されています。もちろん、公式として覚えてしまうのも一方ですが、数学では、覚えて解くのは、あまりお勧めできません。
その立式には、どういう意味があるのか、何か法則はないか、図形的に捉はどんな状態なのかなど、いろいろな方向から、複数のアプローチを考えて記憶していくのが一番良いと思います。
〈例題2〉

〈例題解答例2〉

なお、数学Ⅲを学習の中にある「2回微分」を使うと、この変曲点の意味がより明確になるでしょう。
以下の問題は、極大値と極小値の中点が変曲点であることを用いているので、ぜひ、その有用性を体感してもらえたら幸いです。
〈問題3〉

〈問題解答例3〉

〈問題4〉

〈問題解答例4〉

〈問題4〉

〈問題解答例4〉

