【微積分】 〈13〉 放物線✖️放物線（a/6公式）

　図形によって、囲まれる部分の面積の求め方は様々です。「代数と幾何の一対一対応の美しさ」という観点から観ると、代数的な「関数」から、幾何的な「面積」が求まる「積分」は、まさにその典型です。
　このシリーズでは、複雑な計算になりがちな「積分」について、スピードと確実性のアップを目指して解説します。

---

　前回は、放物線と直線で囲まれた部分の面積を考えました。

　放物線と放物線で囲まれる場合でも、時間と集中力コストを抑えるため、知られている公式を上手に使っていきましょう。

[Method] 放物線✖️放物線＝「1/6公式」＝「a/6公式」

　放物線と放物線で囲まれたフル面積→「1/6公式」or「a/6公式」

---

　この公式では、直線の場合以上に、放物線の２次の係数が１ではなくて残ることが多いので、２次の係数 a を落とさないように注意しましょう。

　また、２交点の端から端までフルフルの面積であるべきことも同様なので、グラフを描いて、フルフルかを確認するように心がけましょう。

---

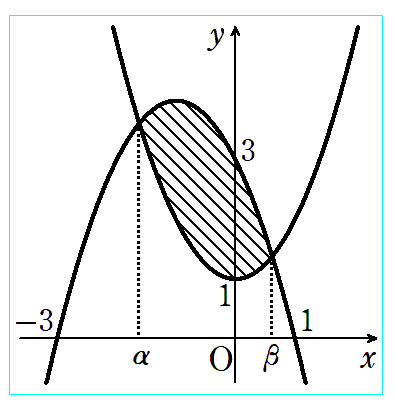
〈例題１〉　

〈例題解答例１〉

---

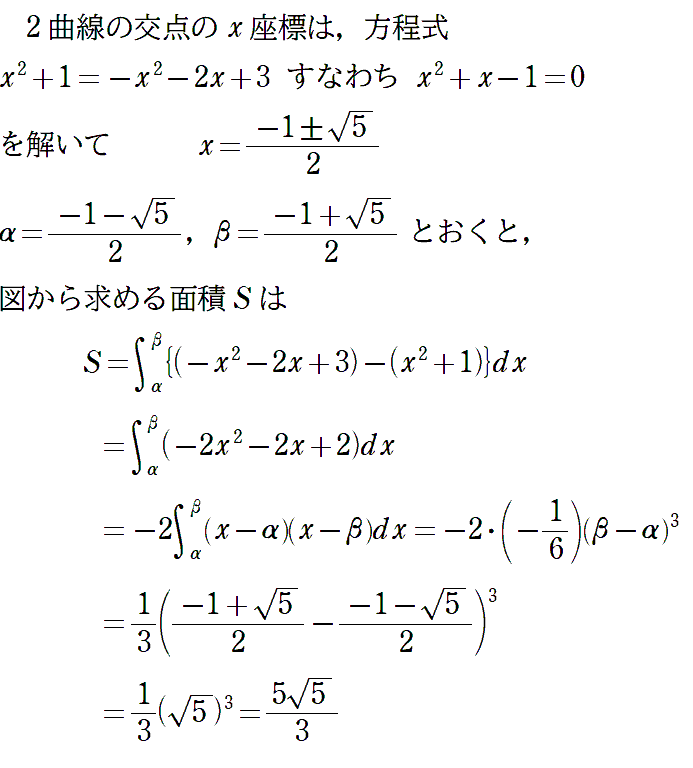
〈問題２〉

〈問題解答例２〉

---

〈問題３〉

〈問題解答例３〉

---

〈問題４〉

〈問題解答例４〉

この解答は、記述の場合においては不十分で、最低限、積分の立式は書いておくほうが良いように思います。ただ、マーク方式など、面積結果のみが必要な場合は、スピード抜群です。