【微積分】 〈12〉 放物線✖️直線（1/6公式）
図形によって、囲まれる部分の面積の求め方は様々です。「代数と幾何の一対一対応の美しさ」という観点から観ると、代数的な「関数」から、幾何的な「面積」が求まる「積分」は、まさにその典型です。
このシリーズでは、複雑な計算になりがちな「積分」について、スピードと確実性のアップを目指して解説します。
前回は、関数のグラフに纏わる条件によって現れる領域について、その面積を積分で求める方法について解説しました。単項式に分けるMethodも紹介しましたが、やはり時間がかかってしまうことは否めません。
時間と集中力コストを抑えるため、知られている公式を上手に使っていきましょう。
[Method] 放物線✖️直線＝「1/6公式」＝「a/6公式」
放物線と直線で囲まれたフル面積→「1/6公式」or「a/6公式」
この公式は、最頻出ではありますが、だからこそ陥りやすいミスもあります。放物線の２次の係数が６分のの分子に残るので、実は、「a/6公式」なのです。２次の係数 a を落とさないように注意しましょう。
そもそも、２交点の端から端までフルフルの面積でないと使えません。途中からの場合はダメなので、グラフを描いて、フルフルかを確認するように心がけましょう。
例えば以下の例では、
左のグラフの場合はOKだけど、右のグラフはダメ！
ｘ＜０の部分が含まれていなくて、フルフルじゃないからね。
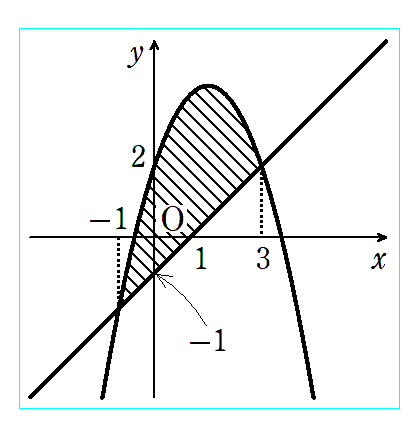
〈例題１〉
〈例題解答例１〉
〈問題２〉
〈問題解答例２〉
〈問題３〉
〈問題解答例３〉
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか？