
転位から塑性理論を理解すること -7-
多結晶構造を前提とした金属材料の塑性変形(結晶塑性)に必要不可欠な存在と言える「転位」について。いわゆる「線欠陥」に分類されますが、原子空孔や不純物原子のように実体的な欠陥ではなく、原子配列の局所的な乱れとして扱われます。

今回は「転位」について、物理現象(変形問題)と関連付けながら、どのような振る舞いがあるのかを見ていければと思います。
前回は原子単位で構成される結晶格子(構造)における転位の振る舞いについて考えました。塑性変形の初期におけるすべり系の起動や、完全転位または部分転位の存在に言及しました。
今回は転位の運動において重要な熱的影響の話をします。これまでは熱に関する物理的条件と結果には言及しませんでした。一方で、原子単位で見たときに熱的影響の代表例として熱振動があります。
前回話したパイエルス応力についても、熱エネルギーによる寄与度を含めると、現実の臨界分解せん断応力は相対的に下がります。このように、熱エネルギーが結晶塑性に及ぼす影響を考えます。

障害物の熱的影響の差異
これまでの転位に関する力学(理論)は絶対零度の場合を想定しています。ここに有限の温度(熱エネルギー)を追加すると、すべりの始動に必要な臨海分解せん断応力は相対的に下がります。
原子の熱振動による熱エネルギーは基本的に温度に比例します。つまり、温度上昇に従い材料の降伏応力(強度)は低下します。
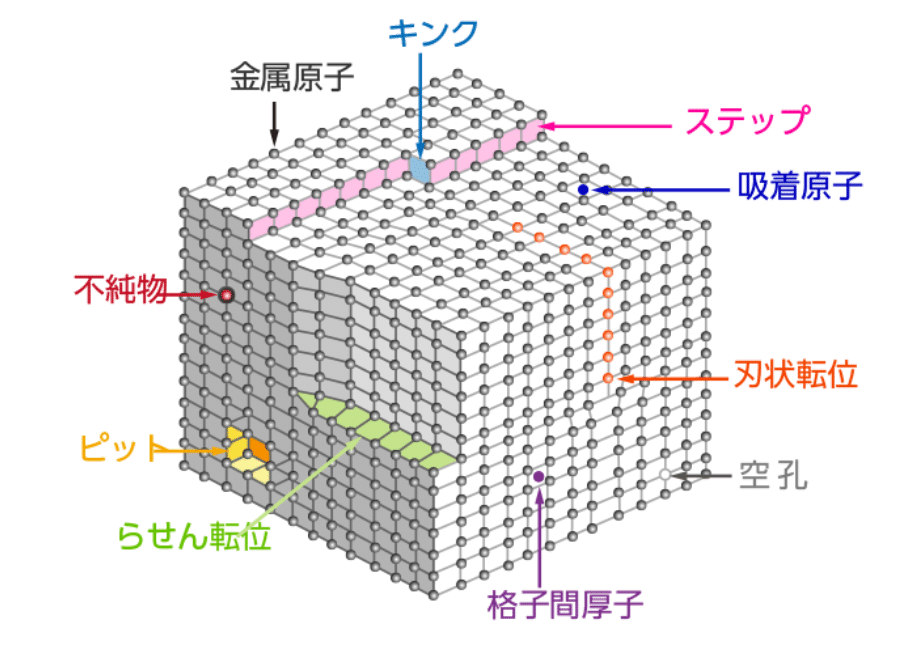
ここで、転位の運動を阻害する障害物は、主に長距離障害物(転位間の相互作用や結晶粒界など)と短距離障害物(固溶原子や析出粒子など)に大別されます。
温度依存性があるのは短距離障害物であり、主に温度と変形速度(せん断ひずみ速度)の関数で表現されます。
$${\tau=\tau_a+\tau_b(T,\.{\gamma})}$$
上記の第1項は長距離障害物による分解せん断応力であり、非熱的応力と呼ばれています。第2項は短距離障害物による分解せん断応力であり、有効応力と呼ばれています。
$${G=\Delta{G}\bigl(1-\frac{\tau_b}{\tau_m}\bigl)}$$
熱活性化エネルギー(G)は外力がゼロの時のエネルギー($${\Delta{G}}$$)に対する減少関数です。また、ここでは絶対零度の臨海分解せん断応力($${\tau_m}$$)が基準になります。

熱活性化過程の定式化
熱活性化における定量評価について書きます。単位時間あたりに熱活性化過程が起こる頻度は次のようになります。
$${p={\nu_D}{\cdot}\frac{b}{L}\exp(-\frac{G}{kT})}$$
ここで、kはボルツマン定数、Lは短距離障害物間の距離、Tは温度です。また、上記(右辺)の係数冒頭は原子の熱振動数であり、弦の振動に由来した補正を掛けています。
熱活性化の単位過程で転位が掃く面積(S)、熱活性化過程の単位体積当たりの発現回数(N)を設けると、転位の変形速度(せん断ひずみ速度)は次のようになります。
$${\.{\gamma}=NSbp=\frac{NS{\cdot}{\nu}_D{b^2}}{L}\exp(-\frac{G}{kT})}$$
また、有効応力は次のようになります。
$${\tau_b=\tau_{m}\bigr\{1-(\frac{MkT}{\Delta{G}})^{\frac{1}{m}}\bigr\}^{\frac{1}{n}}}$$
ここで、 Mは実験などから算出されるパラメータです。また、mは0以上1以下に、nは1以上2以下に規定されるパラメータです。これらは、主に短距離障害物の性質に依存した数値です。
以上のことから、熱活性化エネルギーは有効応力の減少関数です。そして、有効応力は温度上昇に伴い減少します。

熱活性化エンタルピーについて
熱活性化エンタルピーとは、転位が有する熱的影響に寄与するエネルギーです。内部(変形)エネルギーと膨張もしくは収縮するためのエネルギーを合わせたものをいいます。
$${H=G-T\bigl(\frac{\partial G}{\partial T}\bigl)_{\tau_b}=-k\bigr\{\frac{\partial ln(\.\gamma/\.\gamma_0)}{\partial (1/T)}\bigr\}_{\tau_b}}$$
ここで、自然対数中のせん断ひずみ速度の分母に置かれた変数は次の通りに規定されます。
$${\.\gamma_0=\frac{NS{\cdot}{\nu}_D{b^2}}{L}}$$
最後に転位の熱活性化過程における諸量の実験的な求め方についてです。
例えば、高温変形でのクリープ試験のような応力一定状態の材料試験では、変形中に試験温度とせん断ひずみ速度(始点と終点)を測定できれば、熱活性化エンタルピーを次のように求められます。
$${H=k\bigr\{\frac{ln(\.\gamma_1/\.\gamma_2)}{(1/T_2)-(1/T_1)}\bigr\}}$$
ここで、測定可能な物理量の始点は1を、終点は2を添字に使用しています。現実は熱的影響を加味することになるため、上記の考え方が一般的な形になります。

おわりに
今回は転位の運動論について熱的影響を考慮した場合の理論展開を行いました。熱的影響は塑性変形の始動(すべり)に対する追加の要素ですので、絶対零度の場合より現実的な話と言えます。
今回と前回は特に原子単位を添えた場合の転位の運動を見てきました。
次回は巨視的な範囲で、転位の運動と塑性変形ひいては材料特性の結びつきについて、様々な視点から見ていくことにします。
-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------
⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎
⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎
