
転位から塑性理論を理解すること -6-
多結晶構造を前提とした金属材料の塑性変形(結晶塑性)に必要不可欠な存在と言える「転位」について。いわゆる「線欠陥」に分類されますが、原子空孔や不純物原子のように実体的な欠陥ではなく、原子配列の局所的な乱れとして扱われます。
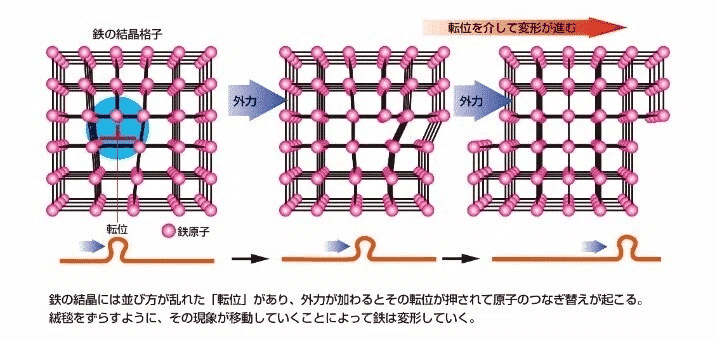
今回は「転位」について、物理現象(変形問題)と関連付けながら、どのような振る舞いがあるのかを見ていければと思います。
前回は転位の増殖や堆積など複数存在する転位群と見做した場合の物理的挙動を見ていきました。
これまでは金属や非金属に関係なく連続体を視点にして、転位の挙動を考えました。ただし、転位は元来で原子の動きに紐付いた存在です。そのため、結晶構造から見た場合も等しく重要です。
今回は原子群の集合体でもある結晶構造から、転位やすべりについて説明することにします。

すべり系とシュミット因子
金属で代表的な結晶構造として3種類あります。鉄やクロムなどが該当する「体心立方格子」と、銅やアルミニウムが該当する「面心立方格子」と、亜鉛やチタンが該当する「稠密六方格子」です。
すべり面とすべり方向を合わせて「すべり系」と呼びます。ここで、すべり面は面間隔が最も大きい最密面で、すべり方向は最近接原子同士を結ぶ最密方向です。

すべり系を場合の数で見たとき、体心立方格子と面心立方格子はそれぞれ12個になります。また、稠密六方格子は3個です。このことから、稠密六方格子を有する金属は他の結晶構造を有する金属に比べて、塑性変形を起こしにくい傾向があります。
次に、複数あるすべり系の中でどれが優先的に働くのかを考えます。円筒形の単結晶試料の単軸引張試験を想定して、任意に設けたすべり系に作用する分解せん断応力を求めます。
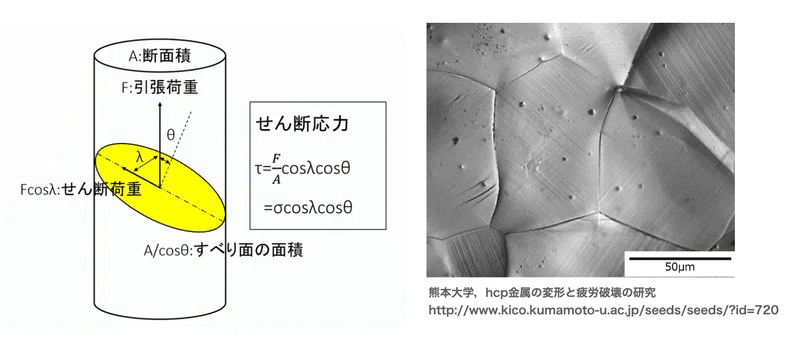
ここで、試料における引張方向とすべり面の法線方向をなす角($${\theta}$$)そして引張方向とすべり方向をなす角($${\lambda}$$)はパラメータと言えます。
$${S_F=cos{\theta}cos{\lambda}}$$
この方位因子を「シュミット因子」と言い、最大値を取るすべり系を「主すべり系」と言います。一般的に、主すべり系が最優先で働きます。
また、シュミット因子が最大値を取るためのパラメータ(条件)が複数存在する場合は、複数のすべり系が同時に働く「多重すべり」に発展します。

部分転位と積層欠陥
バーガースベクトルが結晶格子の並進ベクトルのひとつと一致するとき、その転位は「完全転位」と呼ばれます。また、結晶格子の並進ベクトルと一致しない場合は「部分転位」と呼ばれます。
例えば、2種類以上の原子から構成される合金においては、異種原子が複数で組み合わさることで、別の格子構造を形成します。このとき、複数の部分転位を足し合わせることで、実質的にひとつの完全転位と見做すことがあります。
単独で部分転位が運動したとき、局所的な結晶構造の変化が生じます。その境界に相当する部分を「逆位相境界」と言います。下記はその一例ですが、四酸化三鉄(合金)の逆位相境界を表しています。

単原子金属(結晶)でも部分転位は存在します。完全転位とした場合の運動と部分転位を中継する形の運動をエネルギーで比べると、後者の方が小さいです。これは前回で示したように、転位のエネルギーはバーガースベクトルの2乗に比例すると考えるためです。
一例として、面心立方格子(単結晶)で主すべり系から生じる完全転位を部分転位に分解すると次のようになります。ここで示した転位は特別に「ショックレーの部分転位」と呼ばれます。
$${\frac{a}{2}[\bar{1}01]=\frac{a}{6}[\bar{1}\bar{1}2]+\frac{a}{6}[\bar{2}11]}$$
ここで、aは結晶格子の代表長さです。合金で発生する部分転位は逆位相境界を形成しますが、ショックレーの部分転位は「積層欠陥」を形成します。積層欠陥は局所的な層単位の原子配列の乱れです。ショックレーの部分転位と両者に挟まれた積層欠陥を合わせて「拡張転位」と言います。
逆位相境界と積層欠陥はいずれも面欠陥として扱います。つまり、領域の面積に比例する積層欠陥エネルギーが存在します。また、積層欠陥エネルギーは拡張転位の幅に反比例すると言われています。

転位の駆動力について
転位が運動するには、原子配列の規則性を一旦ですが破る必要があります。原子配列の乱れの生じた不安定な状態なので、ポテンシャルエネルギーとしては運動前に比べて高い状態です。
この状態を克服するために外部から別のエネルギーを供給しますが、それに由来するせん断応力のことを「パイエルス応力」と言います。
$${\tau_p=\frac{2\mu}{1-\nu}\exp{(-\frac{2{\pi}}{1-\nu}{\cdot}\frac{h}{b})}}$$
ここで、hは面間隔です。パイエルス応力は転位の駆動力と言える存在で、その定式化はさらに議論が進んでいますが、面間隔とバーガースベクトル(大きさ)の比であることがポイントです。
一般的に、3種類の結晶格子の中では面心立方格子の積層欠陥エネルギーやパイエルス応力が比較的に小さいと言われています。この点は金属材料の降伏応力の差異にも大きな影響を与えています。

おわりに
今回は材料(構造物)という巨視的なイメージから外れて、微視的な結晶構造の性質を起点に、転位の運動の詳細を見て行きました。転位の運動については、他にも理論的な話題がありますが、今回はここで止めることにします。
次回は同じく原子から見た転位の運動論として、熱的影響(原子の熱振動など)を考慮した場合について考えたいと思います。
-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------
⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎
⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎
