解析学の基礎である微積分の話 -2-

前回に引き続き「解析学」をテーマに書きます。解析学は数学を構成する大きな分野のひとつで、高校数学で学習する「微積分」を本格的に紐解いたものです。

前回は基本の話として微分について取り上げました。

今回は積分について書きます。前回の微分の話が前提となる部分もありますので、同じく参考にしながら読んで頂ければと思います。

数学は私たちから言わせれば「道具」なので、いかに上手く使いこなせるかがポイントです。

積分をイメージで理解する

前回と同様に車の移動を表すモデルを使いながら、積分をイメージで理解していくことにします。

時刻に対する車の速度の情報が手元にあるとして、ある時間的な区間で走行した距離を知りたい。これを求める作業が「積分」です。

車が始点Ｏから終点Ａまで移動します。このとき、時刻に対する車の速度は既知とします。このとき、時間で切り分けた区間（範囲）において車が走行した距離を求める作業が「積分」です。

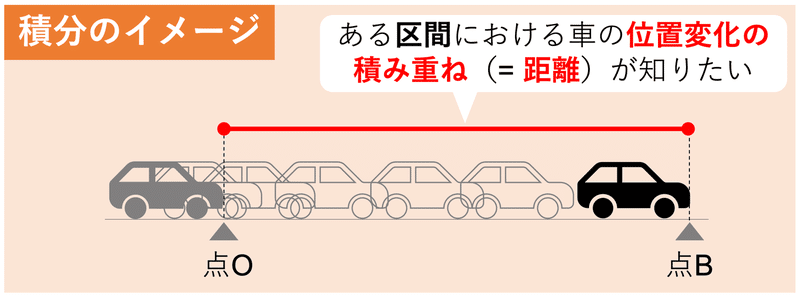
これは指定した時間的な区間における瞬間的な位置の変化（速度）を足し合わせることを意味しています。別の言い方をすると、縦軸（速度）と横軸（時刻）を設けてグラフを描いたときに、指定した区間でグラフを囲んだ際の面積を求めることです。

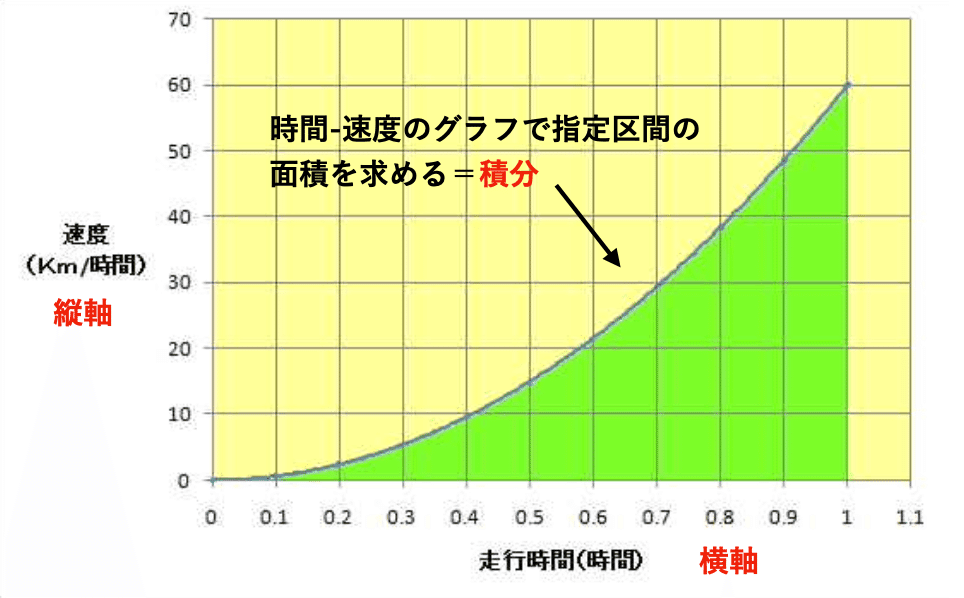
前回に微小な変化量という言葉を用いました。これを今回の積分の話に持ち出すならば「指定区間の中である瞬間の移動距離（微小時間に対する速度と微小時間の積で計算）を全て足し合わせること」になります。

積分の定義について

積分のイメージを掴むために、車の移動のモデルを持ち出しましたが、ここからは具体的な定義について触れていきます。

積分はグラフの横軸の微小量（Δx）と縦軸の値による微小面積を区間の全体で足し合わせたものです。この横軸の微小量（Δx）を限りなくゼロに近づけることで、積分の結果とします。

数値を代入して積分計算を行うことを「定積分」と呼びます。今回は定積分の定義から計算を試みましたが、微分の逆の操作として積分を求める方法もあります。これは「不定積分」と呼ばれます。

実際の計算は数学的なテクニックになりますが、意味をきちんと理解した上でこの先の単元を理解できれば、微積分の面白さに触れられると思います。

微分と積分の相互関係

先ほど微分の逆の操作を積分とすると書きました。これはこれで不定積分の考え方にはなりますが、物理学で利用する際に非常に重要になる考え方です。

運動の法則に代表される変位（距離）と速度と加速度の関係を示します（前回を含めたまとめです）。速度のグラフが中央にありますが、速度を微分すると加速度になります（速度の変化量という意味）。逆に速度を積分すると変位（距離）になります。

このように、微積分の考え方は物理学のいたる所で登場します。具体的には「微分方程式」という形で登場しますが、これだけでも重要な位置付けであることがお分かり頂けると思います。

おわりに

今回は解析学の基礎である微積分において、前回に引き続き積分のことを詳細に説明してみました。

微積分は単なる計算の作業に留まらず、様々な分野の根幹技術に応用されます。特に物理学や工学の面では、より高精度で利便性のある技術の開発などに貢献してきました。

解析学は物理学と密接な関係にある学問です。それは以降で説明することになりますが、今回のように基礎から意味を理解していく必要があるので、しばらくお付き合い頂けたら幸いです。

次回はより実用的な話として、微分方程式について説明します。

-------------------------
最後まで読んで頂き、ありがとうございます。この記事があなたの人生の新たな気づきになれたら幸いです。今後とも宜しくお願いいたします♪♪
-------------------------

⭐︎⭐︎⭐︎ 谷口シンのプロフィール ⭐︎⭐︎⭐︎

⭐︎⭐︎⭐︎ ロードマップ ⭐︎⭐︎⭐︎