
いろいろな三角形の面積の公式と応用
三角形の面積の基本は小学校で習う「底辺×高さ÷2」です。しかし、中学数学、高校数学とやっていくにつれてこの公式から発展した便利な公式がたくさん出てきます。今回はその公式たちと導出を紹介します。
各公式の導出の方針における共通点
公式の紹介の前に、軽く各公式の導出の方針を紹介しておきます。公式はそれぞれいろいろな形をしていますが、導出には割と共通点があります。
パターン① 底辺×高さ÷2の形を作る
まずはおそらく一番メジャーな導出で、基本公式の底辺×高さ÷2の形をどうにかして作るという発想です。基本的に底辺または高さのどちらかの情報が与えられているときによく使われ、残りの情報を与えられている情報だけでどうにかして求めることをします。この残りの情報を求めるときに少し大変な計算をしたりすることがあります。
パターン② 複数の三角形に分割する
これはパターン①ほど多くはありませんが、三角形の内部に何か点があり、それについての情報が与えられたりしているときに有効です。複数の三角形に分割してそれぞれの三角形の面積を求めた後にそれらを合計して求めようという発想です。複数の三角形に分割した後にパターン①を使うこともあると思います。
パターン③ 他の面積の公式の形にする
応用的なものに多いですが、底辺×高さ÷2以外の面積の公式(これから紹介します)の形にするものもあります。その使う公式がパターン①、②のどちらを使って導出されるかは場合によります。パターン③に使用する公式として一番多いものはおそらく公式2の2辺とその間の角から求める公式です。
Lv.1 中学数学までで使える公式
まずは中学数学までで使える公式です。
面倒な計算を簡単にスキップできるものも多く実用的です。
高校数学でもよく出てきます。
※導出は高校数学を使う場合もありますが基本中学数学でできます。
1. 3辺の長さから
3辺から求める公式は私の記事では何度も出てきていますがヘロンの公式です。
$$
三角形の3辺の長さをそれぞれ a,b,c とし、\\s=\dfrac{a+b+c}{2}とおくと、その三角形の面積Sは、\\S=\sqrt{s(s-a)(s-b)(s-c)}
$$
これの変形版として下のようなものもあります。
$$
S=\dfrac{1}{4}\sqrt{2(a^2b^2+b^2c^2+c^2a^2)-(a^4+b^4+c^4)}
$$
導出は下の記事で紹介しています。
導出の方針は主にパターン③です。
この後紹介する「2辺とその間の角から求める公式」を利用して導出されます。高校数学Ⅱまでが分かっていればそこまで難しいものではないので興味がある方は導出にチャレンジしてみてください。変形版に関しては上記の記事の途中から式変形をすることで導出できます。
※中学数学での導出は非常に面倒です。基本は三平方の定理で3辺から三角形の面積を求める方法と全く同じですが、文字で置かれている分大変なものになります。方針としてはパターン①です。
2. 3つの頂点の座標から (xy平面上)
次に座標平面上(xy平面)にある三角形の面積の公式です。
※後ほど極座標での公式も紹介します。
$${xy平面上の3点をそれぞれ (x_1,y_1),(x_2,y_2),(x_3,y_3) とすると、\\その3点を頂点とする三角形の面積Sは、\\S=\dfrac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|\\=\dfrac{1}{2}|y_1(x_2-x_3)+y_2(x_3-x_1)+y_3(x_1-x_2)|\\また、(x_3,y_3)=(0,0)の3頂点のうち1点が原点である三角形は、\\S=\dfrac{1}{2}|x_1y_2-x_2y_1|}$$
$${|A|}$$は$${A}$$の絶対値を表します。
導出は下の記事の「2. 座標平面上の三角形の面積」のところで解説しています。
導出の方針はパターン①の「底辺×高さ÷2の形を作る」です。$${(x_3,y_3)=(0,0)}$$のときはただ代入すればよく、$${y_1,y_2,y_3}$$について整理したほうの式は普通の式変形なので、一番最初の式について導出すればよいのですが、これはベクトルを使うか、$${(x_1,y_1),(x_2,y_2)}$$を通る直線の長さを底辺、その直線と$${(x_3,y_3)}$$の距離が高さなので、それぞれ三平方の定理と点と直線の距離の公式を使うことで求めることができます。かなり大変でしかもあまり面白くないので暇な方以外はやらないことをおすすめします(体験談)。
3. 3辺と外接円の半径から
少し特殊な場合ですが、円に内接している三角形の問題などに有効かもしれません。
$$
三角形の3辺をそれぞれ a,b,c とし、その外接円の半径を R とすると、\\その三角形の面積Sは S=\dfrac{abc}{4R}
$$
導出の方針はパターン③で、使う公式はこれもやはり2辺とその間の角から求める公式です。正弦定理が分かっていれば簡単です。
$${a,bがなす角を\theta とすると、正弦定理より\dfrac{c}{\sin\theta}=2R\\\sin\thetaについて整理すると、\sin\theta=\dfrac{c}{2R}\\2辺とその間の角から面積を求める公式に代入すると、\\S=\dfrac{1}{2}ab\times\dfrac{c}{2R}=\dfrac{abc}{4R}}$$
4. 3辺と内接円の半径から
上のものは3辺と外接円の半径からでしたが、次は3辺と内接円の半径から面積を求める公式です。
$$
三角形の3辺をそれぞれ a,b,c とし、その外接円の半径を r とすると、\\その三角形の面積Sは S=\dfrac{1}{2}r(a+b+c)
$$
外接円は正弦定理という便利なものがあったので割と簡単に導出できましたが、内接円の場合はすこしわかりづらいですね。
内接円の中心は三角形の内心と呼ばれる場所で、その定義は「3角の二等分線の交点」、つまり「3辺からの距離がすべて等しい点」です。もちろん内心は("内接"円の中心ですから)必ず三角形の内部にあるので、3辺のうちいずれかの上にあることは絶対にありません。このため、一般的に直線と点の距離はその点を通る直線の垂線の長さであることを考えると、3辺と内心の距離は内接円の半径と等しいです。このため、パターン②の「複数の三角形に分割する」を使って導出することができます。
分かりやすく図で示しますが、内心Oをとり、そこから各辺まで垂線を引きます。その垂線と各辺との交点との距離は当然内接円の半径に等しいですから$${ r }$$です。これを利用します。
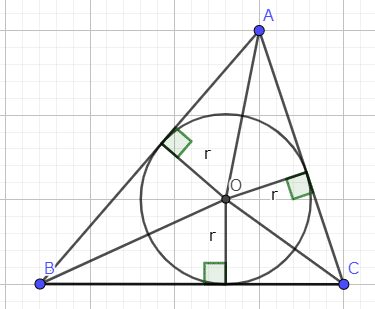
$${△ABC=△AOB+△BOC+△COAとして考える。\\それぞれの三角形の面積は(底辺)×(高さ)×\dfrac{1}{2}で表されるので、\\この場合は(各辺の長さ)×r×\dfrac{1}{2}がそれぞれの三角形の面積になる。\\したがって、S=\dfrac{1}{2}ar+\dfrac{1}{2}br+\dfrac{1}{2}cr=\dfrac{1}{2}r(a+b+c)}$$
今回はパターン②の複数の三角形に分ける方法を用いたあと、分けた三角形の面積を求めるのにパターン①の「底辺×高さ÷2の形を作る」という方法を使いました。このように複数のパターンを使う導出もたまにあります。
5. 正三角形の面積の公式
次は正三角形の面積の公式です。意外と使えます。
$$
一辺 x の正三角形の面積Sは、S=\dfrac{\sqrt{3}}{4}x^2
$$
導出は下の記事の公式に$${n=3}$$を代入することで一発です。
※ただし高校レベルです
中学レベルの導出としてはパターン①で、正三角形のうち1つ頂点を選び、そこからその対辺に垂線を下ろして、その長さを$${h}$$とします。正三角形は二等辺三角形の一種ですから、$${h}$$は対辺を二等分するので、正三角形が2つの合同な直角三角形に分割されます。ここに三平方の定理を適用することで$${h=\dfrac{\sqrt{3}}{2}x}$$ということが分かります。底辺×高さ÷2に形ができたので、公式に代入して求めると$${S=\dfrac{\sqrt{3}}{4}x^2}$$が導出されます。
下のような円に内接する正三角形についての公式もあります。
$$
半径 r の円に内接する正三角形の面積Sは、S=\dfrac{3\sqrt{3}}{4}r^2
$$
これの導出はパターン③で、使う公式は先ほど紹介した外接円と3辺から面積を求める公式です。今回考えるのは正三角形なので、三辺の長さはすべて等しいです。したがって、正三角形の1辺の長さを$${x}$$として公式に代入してみると、$${S=\dfrac{x^3}{4r}}$$となります。$${x}$$の長さですが、三角形を外接円の中心と各頂点を結ぶ線で3分割してみると合同な三角形が3つでき、かつその三角形は底辺が$${x}$$で頂角$${120^{\circ}}$$、長さが$${r}$$である辺が2つある二等辺三角形ですから頂角の2等分線を補助線として引いてみると$${30^{\circ}-60^{\circ}-90^{\circ}}$$の直角三角形ができ、結果的に$${x=\sqrt{3}r}$$となります。これをもとの公式に代入することでこの公式が得られます。
Lv.2 高校文系数学までで使える公式
次からは高校文系数学まで、つまり数学Ⅱまでの知識で使える公式です。
少し使える場面は限られますが、それでもまだ便利だと思います。
6. 2辺の長さとその間の角の大きさから
これは教科書にも載っているレベルの有名な公式です。
$$
三角形の3辺のうち2辺をそれぞれ a,b とし、\\その間の角を\thetaとすると、その三角形の面積Sは、\\S=\dfrac{1}{2} ab\sin\theta
$$
文章だと少しわかりづらいと思うので、下に図を出します。

導出の方針はパターン①の「底辺×高さ÷2の形を作る」です。
底辺の長さはbと分かっているので、辺bから対角に垂線hを引いて高さをaとθで表していきます。

$${正弦定理より、\dfrac{h}{\sin\theta}=\dfrac{a}{\sin90^{\circ}}\\\sin90^{\circ}=1であるから、\sin\thetaを移項すると h=a\sin\theta\\三角形の面積は S=(底辺)×(高さ)×\dfrac{1}{2} であるから、\\S=\dfrac{1}{2}bh=\dfrac{1}{2}b\times a\sin\theta=\dfrac{1}{2}ab\sin\theta}$$
※2辺とその間以外の1角が分かっている場合には三角形は1つに定まらないため面積を求めることはできません。
7. 1辺の長さとその両端の角の大きさから
次に1辺とその両端の角からその三角形の面積を求める公式です。
直接角の大きさが分からなくても角同士の和と差が分かれば求められる便利な公式です。
$$
三角形の3辺のうち1辺をxとし、その両端の角の大きさを\\それぞれa,bとすると、その三角形の面積Sは、\\S=\dfrac{x\sin a\sin b}{2\sin(a+b)}=\dfrac{1}{4}x(\dfrac{\cos(a-b)}{\sin(a+b)}-\dfrac{1}{\tan(a+b)})
$$
導出の方針はパターン③で、使う公式は2辺とその間の角から求める公式です。導出はひたすら三角関数の変形と正弦定理を使っての変形です。この導出では角度はすべてラジアン(弧度法)表記とします。
$${まず、a,b以外のもう1つの角をcとすると、c=\pi-(a+b)\\\angle aを構成している2辺のうちxとは異なるものをyとすると、\\xの対角は\angle c,yの対角は\angle bなので、正弦定理より\dfrac{x}{\sin c}=\dfrac{y}{\sin b}\\したがって、\sin bを左辺に移項するとy=\dfrac{x\sin b}{\sin c}\\x,yの2辺とその間の\angle aの大きさが分かったので、2辺とその間の角から\\面積を求める公式に代入して S=\dfrac{1}{2}xy\sin a=\dfrac{x\sin a\sin b}{2\sin c}\\c=\pi-(a+b)より、\sin c=\sin (\pi-(a+b))=\sin(a+b)\\したがって、S=\dfrac{x\sin a\sin b}{\sin(a+b)}}$$
とりあえず公式のうち1つは導出できましたが、もう1つはひたすら三角関数の変形です。積和公式を知らないとなかなか発想できないような変形を使います。
$${積和公式より、\sin a\sin b=\dfrac{1}{2}(\cos(a-b)-\cos(a+b))\\よって、S=\dfrac{x(\cos(a-b)-\cos(a+b))}{4\sin(a+b)}=\dfrac{1}{4}x(\dfrac{\cos(a-b)}{\sin(a+b)}-\dfrac{\cos(a+b)}{\sin(a+b)})\\a+b=\thetaとおくと、\dfrac{\cos(a+b)}{\sin(a+b)}=\dfrac{\cos\theta}{\sin\theta}=\dfrac{1}{\tan\theta}=\dfrac{1}{\tan(a+b)}\\したがって、S=\dfrac{1}{4}x(\dfrac{\cos(a-b)}{\sin(a+b)}-\dfrac{1}{\tan(a+b)})}$$
積和公式に関しては三角関数の加法定理の応用なので省略します。
Lv.3 高校理系数学までで使える公式
ここまでくるとかなり使える機会は限られてきますが(というかほぼない)、高校理系数学、つまり数Bと数Ⅲの範囲で習う知識から使える公式です。
8. ベクトルを用いた三角形の面積の公式
高校理系数学といえばベクトル、といっても過言ではないほどしつこく付き纏ってくる(?)ベクトルですが、三角形のうち2辺のベクトルの情報(それぞれの大きさと内積)があればその三角形の面積も求めることができます。
$$
△ABCの面積Sは、S=\dfrac{1}{2}\sqrt{|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2-(\overrightarrow{AB}\cdot\overrightarrow{AC})^2}
$$
導出方針はパターン③で、使う公式は2辺とその間の角から面積を求める公式です。といっても、ただの三角関数の変形なのでベクトルの基本がわかっていれば簡単です。
$${|\overrightarrow{AB}|と|\overrightarrow{AC}|は2辺の長さなので、\thetaを2つのベクトルがなす角とすると\\三角形の面積は公式に代入してS=\dfrac{1}{2}|\overrightarrow{AB}|\cdot|\overrightarrow{AC}|\cdot\sin\theta\\ここで、\sin^2\theta=1-\cos^2\thetaより\sin\theta=\sqrt{1-\cos^2\theta} …(※)\\よって、S=\dfrac{1}{2}|\overrightarrow{AB}|\cdot|\overrightarrow{AC}|\cdot\sqrt{1-\cos^2\theta}\\これを変形し、S=\dfrac{1}{2}\sqrt{|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2-|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2\cos^2\theta}\\|\overrightarrow{AB}||\overrightarrow{AC}|\cos\theta=\overrightarrow{AB}\cdot\overrightarrow{AC}より、S=\dfrac{1}{2}\sqrt{|\overrightarrow{AB}|^2|\overrightarrow{AC}|^2-(\overrightarrow{AB}\cdot\overrightarrow{AC})^2}}$$
導出の途中の(※)ですが、本来は$${\sin\theta=\pm\sqrt{1-\cos^2\theta}}$$としなければいけないところです。しかし、今回の場合はマイナスにするとベクトルの大きさは正の値になることから面積がマイナスになってしまいます。したがって$${\sin\theta>0}$$なので、$${\sin\theta=\sqrt{1-\cos^2\theta}}$$で大丈夫です。
9. 3つの頂点の座標から (極座標系)
次に極座標系での3頂点の座標からの面積の公式です。
$$
極座標上の3点を (r_1,\theta_1),(r_2,\theta_2),(r_3,\theta_3) とすると、\\その3点を頂点とする三角形の面積Sは、\\S=\dfrac{1}{2}|r_1r_2\sin(\theta_2-\theta_1)+r_2r_3\sin(\theta_3-\theta_2)+r_3r_1\sin(\theta_1-\theta_3)|\\特に、(r_3,\theta_3)が極と一致する場合は\\S=\dfrac{1}{2}r_1r_2|\sin(\theta_1-\theta_2)|=\dfrac{1}{2}r_1r_2|\sin(\theta_2-\theta_1)|
$$
導出の方針はパターン③で、使う公式は先ほど紹介したxy平面上の3点から面積を求める公式です。xy平面上の座標を極座標に変換するという強引な方法で導出します。
$${まず、xy平面上の3点から面積を求める公式より、\\S=\dfrac{1}{2}|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|\\=\dfrac{1}{2}|x_1y_2-x_1y_3+x_2y_3-x_2y_1+x_3y_1-x_3y_2|\\ここで、x=r\cos\theta,y=r\sin\thetaとおくことで極座標に変換できる。\\S=\dfrac{1}{2}|x_1y_2-x_1y_3+x_2y_3-x_2y_1+x_3y_1-x_3y_2|\\=\dfrac{1}{2}|r_1r_2\sin\theta_2\cos\theta_1-r_1r_3\sin\theta_3\cos\theta_1+r_2r_3\sin\theta_3\cos\theta_2-r_1r_2\sin\theta_1\cos\theta_2+r_1r_3\sin\theta_1\cos\theta_3-r_2r_3\sin\theta_2\cos\theta_3|\\=\dfrac{1}{2}|r_1r_2(\sin\theta_2\cos\theta_1-\sin\theta_1\cos\theta_2)+r_2r_3(\sin\theta_3\cos\theta_2-\sin\theta_2\cos\theta_3)+r_3r_1(\sin\theta_1\cos\theta_3-\sin\theta_3\cos\theta_1)|\\それぞれに三角関数の加法定理を使うと、\\S=\dfrac{1}{2}|r_1r_2\sin(\theta_2-\theta_1)+r_2r_3\sin(\theta_3-\theta_2)+r_3r_1\sin(\theta_1-\theta_3)|}$$
次に極と他の2点を通る場合の導出です。
$${1点が極と一致するということはr_3=0ということなので、…(*)\\先ほど導出した公式に代入すると、S=\dfrac{1}{2}r_1r_2|\sin(\theta_1-\theta_2)|\\一般的に\sin(-\alpha)=-\sin\alphaであるから、|\sin(-\alpha)|=|\sin\alpha|\\よって、|\sin(\theta_1-\theta_2)|=|\sin(-(\theta_1-\theta_2))|=|\sin(\theta_2-\theta_1)|\\このことから、S=\dfrac{1}{2}r_1r_2|\sin(\theta_1-\theta_2)|=\dfrac{1}{2}r_1r_2|\sin(\theta_2-\theta_1)}$$
$${(*)}$$の部分に関しては$${r_3=0}$$としていますが、偏角$${\theta_3}$$に関してはどのような値でもよいです。極座標の平面を考えるとわかりますが、$${r_3=0}$$ということは極と一致するので、角度によって位置が変わるなどということはありません。また、公式に代入するときも$${\theta_3}$$に関しては$${r_3=0}$$ですべて消されているので考える必要はありません。
Lv.4 大学数学以上?
もうここまでくると用法は不明です。何言ってるかわからないくらいが正常だと思います。
10. 球面上の三角形の面積
最後に球面上の三角形の面積の紹介です。多分使い道はない。
$$
半径 r の球面上に三角形をとり、その角の大きさを\\それぞれ a,b,cとすると、その三角形の面積Sは、\\S=(a+b+c-\pi)r^2 (ただし、a,b,cはラジアン表記)
$$
導出の方針は紹介したパターンにはありませんが、考え方は簡単です(ただし導出が簡単とは一言も言っていない)。半径$${r}$$の球の表面積が$${4\pi r^2}$$であるということは中学生で習います。ここから、扇形の面積のときと同じような発想で、球面上の三角形を「球の表面積の一部」として考えます。パターン②に近いですが、球面を複数の部分に分けて考えます。この導出自体はかなり簡略化したものなので中学生でもおそらく理解できると思いますが、厳密に導出をしたい場合は積分などの専門的な知識が必要です。
まずはこのような図を考えます。ここで、△ABCについて考えます。

したがって、△ABC≡△A'B'C'が成り立つ。
※以下、領域に関する定義としてはすべて小さいほうとします。
$${A-B-A'-Cで囲まれた弓状の領域を\alpha,\\B-A-B'-Cで囲まれた弓状の領域を\beta,\\C-A-C'-Bで囲まれた弓状の領域を\gamma,\\\triangle ABCの領域(面積)をSとする。\\ここで、各点の対称性を考えるとA'-B'-A-C'=\alpha,\\B'-A'-B-C'=\beta,C'-A'-C-B'=\gamma,\triangle A'B'C'=S\\ここで2(\alpha+\beta+\gamma)を考えると、その値は(球の表面積)+4Sである。\\したがって、2(\alpha+\beta+\gamma)-4S=4\pi r^2より、\alpha+\beta+\gamma-2S=2\pi r^2}$$
次に、具体的な$${\alpha,\beta,\gamma}$$の値を$${a,b,c}$$で表していきます。

αで表される部分は青色で示している。
$${青で示された場所は半径rの2乗と角度aの積に比例するので、\\比例定数Mを用いて\alpha=Mar^2と表せ、それが2つ分で2Mar^2\\\pi-aのほうの弓形領域はMr^2(\pi-a)で、それが2つ分で2Mr^2(\pi-a)\\この和が球の表面積と等しいので 2Mar^2+2Mr^2(\pi-a)=4\pi r^2\\これをMについて解いて、M=2\\したがって、\alpha=2ar^2\\同様に、\beta=2br^2,\gamma=2cr^2}$$
※厳密に比例すると証明するためには球面の面積を極座標積分して計算する必要があります。大変なのでここでは省略します。
$${\alpha,\beta,\gamma}$$の具体値が求まったので、あとは代入して$${S}$$について解くだけです。
$${\alpha+\beta+\gamma-2S=2\pi r^2より、\alpha,\beta,\gammaを代入して\\2ar^2+2br^2+2cr^2-2S=2\pi r^2\\Sについて整理すると、S=(a+b+c-\pi)r^2}$$
このように、詳しいことを考えたりしなければ難しい知識を使う必要なく導出できますが、厳密に導出をしたいならば高校理系数学または大学数学を使うことになります。
少し発展ですが、$${a+b+c}$$の値について考えてみましょう。一般的に面積の値は正にならなければならないので、$${(a+b+c-\pi)r^2>0}$$です。掛けて正になるのは同符号のみなので、($${a+b+c-\pi>0}$$かつ$${r^2>0}$$)または($${(a+b+c-\pi)<0}$$かつ$${r^2<0}$$)の2択しかありませんが、$${r}$$は球の半径なので当然正の実数であることより$${r^2>0}$$しかありえません。したがって、$${a+b+c-\pi>0}$$より、$${a+b+c>\pi}$$、つまり、$${a+b+c>180^{\circ}}$$であることになります。
このことから、球面上にある三角形の内角の和は必ずしも1つに定まるわけではなく、しかもその値は$${180^{\circ}}$$より大きくなることが分かります。
【発展】面積の公式の応用例
ここで紹介した面積の公式にはあまり多くはありませんが応用例があります。少し紹介しておきます。
(1) ブラーマグプタの公式
ブラーマグプタの公式は円に内接する四角形の面積の公式です。ヘロンの公式ととてもよく似た形をしています。
$$
円に内接する四角形の4辺をそれぞれ a,b,c,d とし、\\s=\dfrac{a+b+c+d}{2}とおくと、その四角形の面積Sは、\\S=\sqrt{(s-a)(s-b)(s-c)(s-d)}
$$
導出は書きませんが、下のように補助線を円の外部に引くことで相似な三角形が現れ、比の関係性からヘロンの公式を用いて変形できます。

(2) 正多角形の面積の公式
次に正多角形の面積の公式です。
$$
一辺の長さが x の正 n 角形の面積Sは、\\S=\dfrac{nx^2}{4\tan\frac{\pi}{n}}
$$
導出に関しては下の記事で紹介しています。
導出方針はパターン②とパターン③です。具体的には複数の三角形に分割した後に$${S=\dfrac{1}{2}ab\sin\theta}$$を利用します。
今回はいろいろな三角形の面積の公式の紹介でした。使えそうだと思ったらぜひ覚えて使ってみてください!
