せまゲー生半可集（８）～アブストラクトゲーム『Glaisher』よりもヤヤコシソーな、『Ackermann（仮）』を考えてみる（前編）

前回の記事はこちら。

今回は、ちょっとオリジナルになるかも知れないせまゲーを考えてみようと思います。

Glaisher

『Glaisher（グレーシャー）』は、正田謙さんが考案し、２０１５年にNestorgamesで発売されたアブストラクトゲームです。

Glaisher

タイトルの由来は、スタックされたコマを（分割して）移動するルールのコンセプトが、数学者のジェームズ・グレーシャーさんが研究した整数分割定理（グレーシャーの定理）から得たことのようです。
また、この移動ルールは、ペンシルパズルの「カックロ」のルールとも言いかえられます。

カックロ - Wikipedia

ところで、ジェームズ・グレーシャーさんですが、日本版Wikipediaで検索してみると、（気球大好き気象学者の）お兄さんが出てきます。

ジェームズ・グレーシャー - Wikipedia

英語版Wikipediaでは、James Whitbread Lee Glaisher（ジェームズ・ウィットブレッド・リー・グレーシャー）で、見つけることができます。

James Whitbread Lee Glaisher - Wikipedia

『グレーシャー』は、ラディアスリーのYoutube『アブな世界』でも第１２回に収録されています。

アブ大の履修科目認定は、最難の４年どころか卒業論文研究対象に値するというなかなかに歯ごたえのある評価となっています。

『グレーシャー』の日本語ルールはBoardgamegeekにPDFファイルがアップされています。

Glaisher Rules in Japanese | Glaisher

さて、『グレーシャー』は数学の定理から着想して考案されたアブストラクトゲームですが、他にもなにか数学まわりのネタからゲームルールのアイデアが見つけだせるでしょう。

結果、今回試してみるのが、

アッカーマン関数（Ackermann Function）

なのです。

アッカーマン関数 - Wikipedia

アッカーマン関数とは

アッカーマン関数は、特定のジャンルにおいて、こすり倒すぐらいあまりにも有名です。
そのそのジャンルとは

巨大数

です。

巨大数 - Wikipedia

大きな数といえば、那由多（なゆた）とか阿僧祇（あそうぎ）とか恒河沙（ごうがしゃ）とか不可思議（ふかしぎ）とか無量大数（むりょうたいすう）とか連想すると思います。
そんなもん、小さすぎます。

巨大数を考えるコミュニティでは、もっととんでもないことになっています。
その辺の事情は、巨大数研究Wiki、ならびに、書籍『巨大数論』などを覗いてみてください。

巨大数研究 Wiki

巨大数論

さて、本題。
アッカーマン関数とは、０以上の整数 m と n に対し、

$$
A(n,m) = \begin{cases}
m-1, &\text{if } m=0 \\
A(n,m-1), &\text{if } n=0 \\
A(n-1,A(n,m-1)), &\text{otherwise }
\end{cases}
$$

によって定義される関数です。

【注記】
上記の式はWikipediaより引用しましたが、ｍとｎを交換して表記しています。
交換した理由・意図は、今後の記事の内容で、後々明らかになります。
ご了承ください。

アッカーマン関数は、ｍもｎも小さい値だと、そんなに大きな数にはなりません。
例えば、A(3,3)を計算した値は６１です。
６１は、結構そそる垂涎モノの数字です。
というのも、一辺５マスの正六角形マスの盤面のマスの数が６１なのです。

一辺４マスの正三角形（１０マス）を
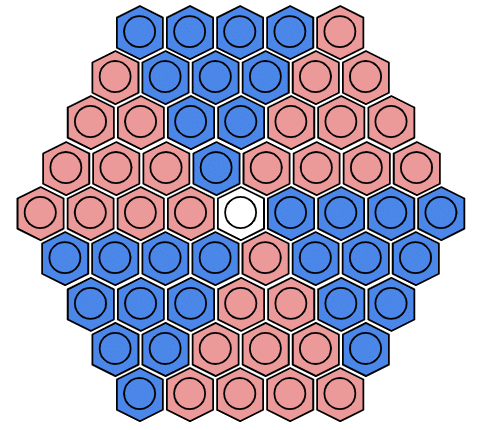
６組組み合わせて、中央に１マス
加えると、一辺５マスの正六角形になる。

A(3,3)のカッコ内の数字を、ちょっと大きくしてみましょうか。

A(3,4)だと、１２５になります。
そんなに大きくなりませんね。
では、数字を入れ替えてA(4,3)だと、

$$
2^{2^{65536}}-3
$$

です。
……なんのことやらですが、なんとなく不穏です。

$$
2^{65536}
$$

は、２×２×２×………×２と、２を６５５３６回掛けた数です。
計算すると、２万桁より若干少ない（１９７００桁くらい）です。

$$
2^{2^{65536}}
$$

は、２×２×２×………×２と、２をさっき計算した２万桁より若干少ない回数分掛けた数です。
一体何桁の数字なのでしょうか。
もう何がなんだかわかりません。

実際に計算してみる

A(3,3)=61ですが、実際に計算するとその値になるのでしょうか？
その計算過程をすべて載せたマンガがあります。

寿司 虚空編

小林銅蟲さんの『寿司　虚空編』です。
寿司やグルメの料理マンガではありません。

巨大数マンガ

です。
こちらの第２話で、１０ページに渡り、フォントサイズがポイント１（もしくはそれ以下）で印刷されております。
ポイント１となると、文字の大きさは米粒に写経するレベルです。
はたして何千回計算しているのか、もうよくわかりません。

なので、ちょっと自分ももう少し小さな数で実際に計算してみることにしました。
A(3,1)=13なので、数千回もかからないと思います。

その計算過程の結果ですが……

……覚悟はできましたね……

……では、どうぞ。

A(3,1)
= A(2,A(3,0))
= A(2,A(2,1))
= A(2,A(1,A(2,0)))
= A(2,A(1,A(1,1)))
= A(2,A(1,A(0,A(1,0))))
= A(2,A(1,A(0,A(0,1))))
= A(2,A(1,A(0,2)))
= A(2,A(1,3))
= A(2,A(0,A(1,2)))
= A(2,A(0,A(0,A(1,1))))
= A(2,A(0,A(0,A(0,A(1,0)))))
= A(2,A(0,A(0,A(0,A(0,1)))))
= A(2,A(0,A(0,A(0,2))))
= A(2,A(0,A(0,3)))
= A(2,A(0,4))
= A(2,5)
= A(1,A(2,4))
= A(1,A(1,A(2,3)))
= A(1,A(1,A(1,A(2,2))))
= A(1,A(1,A(1,A(1,A(2,1)))))
= A(1,A(1,A(1,A(1,A(1,A(2,0))))))
= A(1,A(1,A(1,A(1,A(1,A(1,1))))))
= A(1,A(1,A(1,A(1,A(1,A(0,A(1,0)))))))
= A(1,A(1,A(1,A(1,A(1,A(0,A(0,1)))))))
= A(1,A(1,A(1,A(1,A(1,A(0,2))))))
= A(1,A(1,A(1,A(1,A(1,3)))))
= A(1,A(1,A(1,A(1,A(0,A(1,2)))))))
= A(1,A(1,A(1,A(1,A(0,A(0,A(1,1))))))))
= A(1,A(1,A(1,A(1,A(0,A(0,A(0,A(1,0)))))))))
= A(1,A(1,A(1,A(1,A(0,A(0,A(0,A(0,1)))))))))
= A(1,A(1,A(1,A(1,A(0,A(0,A(0,2)))))))
= A(1,A(1,A(1,A(1,A(0,A(0,3))))))
= A(1,A(1,A(1,A(1,A(0,4)))))
= A(1,A(1,A(1,A(1,5))))
= A(1,A(1,A(1,A(0,A(1,4)))))
= A(1,A(1,A(1,A(0,A(0,A(1,3))))))
= A(1,A(1,A(1,A(0,A(0,A(0,A(1,2)))))))
= A(1,A(1,A(1,A(0,A(0,A(0,A(0,A(1,1))))))))
= A(1,A(1,A(1,A(0,A(0,A(0,A(0,A(0,A(1,0)))))))))
= A(1,A(1,A(1,A(0,A(0,A(0,A(0,A(0,A(0,1)))))))))
= A(1,A(1,A(1,A(0,A(0,A(0,A(0,A(0,2))))))))
= A(1,A(1,A(1,A(0,A(0,A(0,A(0,3)))))))
= A(1,A(1,A(1,A(0,A(0,A(0,4))))))
= A(1,A(1,A(1,A(0,A(0,5)))))
= A(1,A(1,A(1,A(0,6))))
= A(1,A(1,A(1,7)))
= A(1,A(1,A(0,A(1,6))))
= A(1,A(1,A(0,A(0,A(1,5)))))
= A(1,A(1,A(0,A(0,A(0,A(1,4))))))
= A(1,A(1,A(0,A(0,A(0,A(0,A(1,3)))))))
= A(1,A(1,A(0,A(0,A(0,A(0,A(0,A(1,2))))))))
= A(1,A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(1,1)))))))))
= A(1,A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(1,0))))))))))
= A(1,A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,1))))))))))
= A(1,A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(0,2)))))))))
= A(1,A(1,A(0,A(0,A(0,A(0,A(0,A(0,3))))))))
= A(1,A(1,A(0,A(0,A(0,A(0,A(0,4)))))))
= A(1,A(1,A(0,A(0,A(0,A(0,5))))))
= A(1,A(1,A(0,A(0,A(0,6)))))
= A(1,A(1,A(0,A(0,7))))
= A(1,A(1,A(0,8)))
= A(1,A(1,9))
= A(1,A(0,A(1,8)))
= A(1,A(0,A(0,A(1,7))))
= A(1,A(0,A(0,A(0,A(1,6)))))
= A(1,A(0,A(0,A(0,A(0,A(1,5))))))
= A(1,A(0,A(0,A(0,A(0,A(0,A(1,4)))))))
= A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(1,3))))))))
= A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(1,2)))))))))
= A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(1,1))))))))))
= A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(1,0)))))))))))
= A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,1)))))))))))
= A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,2))))))))))
= A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,3)))))))))
= A(1,A(0,A(0,A(0,A(0,A(0,A(0,A(0,4))))))))
= A(1,A(0,A(0,A(0,A(0,A(0,A(0,5)))))))
= A(1,A(0,A(0,A(0,A(0,A(0,6))))))
= A(1,A(0,A(0,A(0,A(0,7)))))
= A(1,A(0,A(0,A(0,8))))
= A(1,A(0,A(0,9)))
= A(1,A(0,10))
= A(1,11)
= A(0,A(1,10))
= A(0,A(0,A(1,9)))
= A(0,A(0,A(0,A(1,8))))
= A(0,A(0,A(0,A(0,A(1,7)))))
= A(0,A(0,A(0,A(0,A(0,A(1,6))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(1,5)))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(1,4))))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(1,3)))))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(1,2))))))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(1,1)))))))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(1,0))))))))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,1))))))))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,2)))))))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,3))))))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,4)))))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,A(0,5))))))))
= A(0,A(0,A(0,A(0,A(0,A(0,A(0,6)))))))
= A(0,A(0,A(0,A(0,A(0,A(0,7))))))
= A(0,A(0,A(0,A(0,A(0,8)))))
= A(0,A(0,A(0,A(0,9))))
= A(0,A(0,A(0,10)))
= A(0,A(0,11))
= A(0,12)
= 13

です。
１０６回計算しました。
左右のカッコの数が揃っているのか、全く自信がありません。
ちょっとしたプチ寿司虚空感です。

締め

ということで、次回はこのヤヤコシーなアッカーマン関数からボードゲームのルールを考えてみます。

では。