
せまゲー生半可集(9)~アブストラクトゲーム『Glaisher』よりもヤヤコシソーな、『Ackermann(仮)』を考えてみる(後編)
前回の記事はこちら。
ともかく卒倒しそうなアッカーマン関数を紹介しました。
アッカーマン関数は、以下の式で定義されます。
$$
A(n,m) = \begin{cases}
m-1, &\text{if } m=0 \\
A(n,m-1), &\text{if } n=0 \\
A(n-1,A(n,m-1)), &\text{otherwise }
\end{cases}
$$
今回は、この関数をボードゲームのルールとして取り入れてみます。
アッカーマン関数を図示してみる
前回は実際にA(3,1)を手で計算してみました。
やってみて感じたのですが、以前なにか経験したことあるな、と。
あれだ。
マンカラ一人勝ち問題でした。
延々と穴が続くマンカラで、延々と石を入れ続けていました。
で、この経験とアッカーマン関数が重なったときに、ふと、思いついたのです。
アッカーマン関数の
カッコ内の2つの数を
コマにしたらどうなるのか?
例えばA(3,2)を以下のようにあらわします。

左側の数字は大きなコマ(緑)で、右側の数字は小さなコマ(オレンジ)になります。
A(3,2)=A(2,A(3,1))となりますが、図示するとこんな感じです。

(1) 隣のマスに、大きなコマを1個だけ少なくストック。
(2) 一番上の大きなコマを小さなコマごと隣のマスにスライド移動。
(3) 移動したあとのストックから、小さなコマを1個取りのぞきます。
ちょっと込み入ったプロセスですが、そんなに複雑ではありません。
$$
A(n,m) = \begin{cases}
m-1, &\text{if } m=0 \\
A(n,m-1), &\text{if } n=0 \\
A(n-1,A(n,m-1)), &\text{otherwise }
\end{cases}
$$
先ほどのA(3,2)の計算は、一番下のotherwiseの場合の式を使いました。
では、他のm=0やn=0の場合の、コマの動きはどうなるでしょうかね。
実際に図示しながらA(3,0)を計算してみます。
※以下の図のコマの下にある赤線は、マスになります。



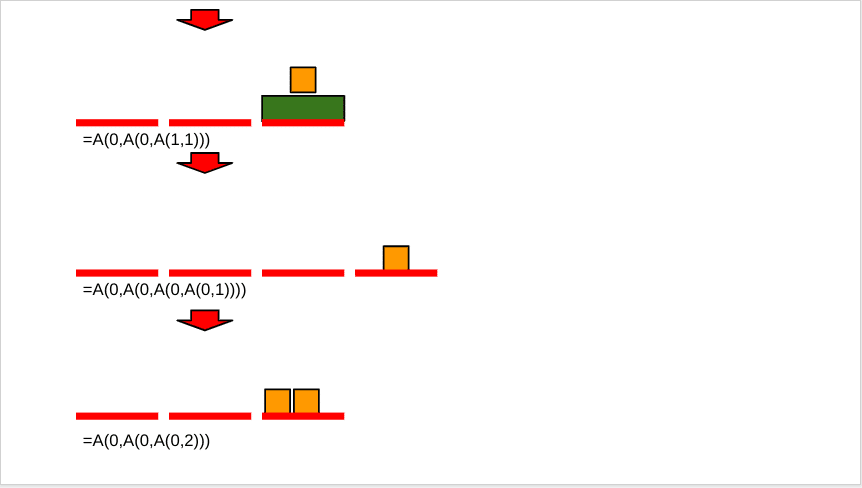

結果、A(3,0)=5となります。
$$
A(n,m) = \begin{cases}
m-1, &\text{if } m=0 \\
A(n,m-1), &\text{if } n=0 \\
A(n-1,A(n,m-1)), &\text{otherwise }
\end{cases}
$$
アッカーマン関数の一番上の式、m=0の場合(例えば、A(3,0)=A(2,1))は、ストックにある1番上の大きなコマを小さなコマに交換することです。
アッカーマン関数の真ん中の式、n=0の場合(例えば、A(0,A(0,3))=A(0,4))は、小さなコマだけのストックを、増やす時とは逆の方向に移動して、小さなコマをもう1つ追加することです。
図示してみると気づいたのですが、一次元盤面でコマをルールに沿って動かしているアッカーマン関数は、それ自体で
せまゲー
です。
実は計算しているのではなく、本当は遊んでいました。
アッカーマン関数のせまゲー化
アッカーマン関数の計算は、一次元盤面でコマを動かすことに置き換えることができました。
もし、平面(二次元)配列の盤面でコマを動かすとしたら、どうなるでしょうか。
一次元では(逆方向も含めて)一方向にしか移動できませんが、平面だと複数方向に移動できます。

【例】
青の矢印方向は、
・赤の矢印方向とは異なるマスへ、スタックを移動させる。
・移動後に残った大きいコマしかないスタックをコマ交換する。
と、赤の矢印方向とは別の選択肢も可能であることを示しています。
おそらくですが、コマのアクションのルールをまとめておけば、適当な盤面とコマの初期配置があれば、なんとなくゲームになりそうに思われます。
アッカーマン関数は、3つの式をカッコ内の数字(n,m)によって場合分けします。
カッコ内の数字(n,m)の左側と右側をコマとして表現しましたが、それらにに名称をつけてみます。
左側にあたる大きいコマを「Nebula(ネビュラ)」、右側に当たる小さいコマを「Meta(メタ)」とします。
【補足】
前回、Wikipediaから引用したアッカーマン関数を元にして、本noteではmとnを入れ替えていることをお断りしておりました。
実は、コマの名称の頭文字(nとm)を揃えるためでした。
コマの移動のアクション3種類にも名称をつけます。
(1)Metaverse(メタバース)
アッカーマン関数では、m=0の場合(A(n,0)=A(n-1,0))の式に相当します。

ネビュラだけのスタックのマスでのアクションとなります。
一番上のネビュラをメタと交換します。
(2)Multiverse(マルチバース)
アッカーマン関数では、otherwiseの場合(A(n,m)=A(n-1,A(n,m-1))の式に相当します。

1個以上のネビュラと1個以上のメタのあるスタックでのアクションです。
隣接した空きマスに、スタックの一部を移動させて、新しいスタックを作ります【※その際、ネビュラを追加したり、メタを除外したりします。アクションのイメージは、本記事の前半で書きましたので参照してください】。
(3)Inverse(インバース)
アッカーマン関数では、n=0の場合(A(0,n)=n+1)の式に相当します。

メタだけのスタックのマスでのアクションとなります。
隣接したマスにスタックを移動して、さらにもう1個メタを追加します。
移動前のマスはゲームから除外します【※その理由は、除外しないと移動前の空きマスへ再度移動できることとなり、これを繰り返すと、無限にメタ(小さいコマ)を生み出し続けます。一種の千日手状態となりえるので、制御のためマス除外のルールを加えます(実際、アッカーマン関数の計算過程でも、マスの除外と類似したことが起きています)】。
ちなみに、隣接したマスにネビュラやメタがあっても、Inverseができます。

アクションの名称をメタバース・マルチバース・メタバースとしたのは、イメージと語呂がなんとなく揃いそうなので。
盤面ですが、マスが適当に隣接して、コマの移動のアクションに支障をきたさず、適当なマス数(最初は、数マス〜十数マス)があれば、何でもいいと思います。
例えば、Wikipediaの平面充填から適当に取ってきても構いません。
正六角形でも、正方形でも、三角形でもOKです。
複数の正多角形の組み合わせも、ペンローズタイルもOKです。

右は、カイロ五角形の14マス
初期配置も、適当にスタックを2個3個置くことで、なんとかなります。
ゲームのプレイと勝敗は、2人のプレイヤーが互いに手番(アクションを1回行う)を回し、手番でアクションができなくなったプレイヤーの負けです。
つまり、プレイヤー全員が同じアクションを行う不偏ゲーム、せまゲーです。
テストプレイ
ちゃんとゲームになっているのか、試しに遊んでみます。
今回は、以下の盤面と初期配置です。

正六角形マス9個の組合せの盤面です。
ネビュラ2個とメタ3個のスタック1個(アッカーマン関数だとA(2,3))を配置しました。
以下、どのようなアクション(Metaverse・Multiverse・Inverse)をしたか示しつつ、一手一手記譜を描いていきます。
【差し替えとおまけ:2023/02/24】
本記事を2月22日にアップ後、加藤香流さんより、記譜中に誤ったアクションをしている箇所がある指摘を受けまして、差し替えました。
差し替え前の誤ったアクションの記譜を、おまけとして記事の最後に残しておきましたので、参考にしていただけると幸いです。
【追記:2023/02/26】
さらに、19手目の記譜に誤りがありましたので、修正いたしました。
再び加藤香流さんに感謝申し上げます。


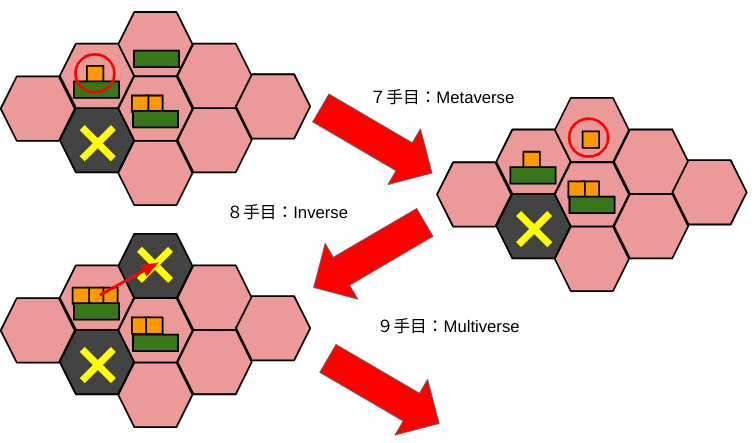





以上、後手の手番でコマを動かすことができないので、先手の勝ちとなります。
Metaverseは、空きコマの数は減りません。
Multiverseはネビュラが2個以上あれば空きコマが減ります(1個の場合は10手目のように減らない)。
Inverseは、盤面のマスを削除、あるいは盤面を分断して複数のマスにコマが移動できないように操作できます。
つまり、終了に向けて収束しているので、なんとなくゲームになっています。
締め
以上、アッカーマン関数から新しいせまゲーを考案しました。
改めてタイトルですが、盤面をアクションに合わせて「Universe」と呼ぶことにしまして、
『Ackermann’s Universe(アッカーマンの宇宙)』
と名付けたいと思います。
とりあえずのルールを用意しましたが、さまざまなバリアントルールが考えられると思います。
適当にいじって自由に変更して遊んでくださいませ。
では。
【おまけ:2022/02/24】
差し替え前のテストプレイです。
5手目と8手目のInverseは、メタをもう1個追加しないといけません。
戒めとして気をつけましょうね、ということで失敗した記譜を残しておきます。
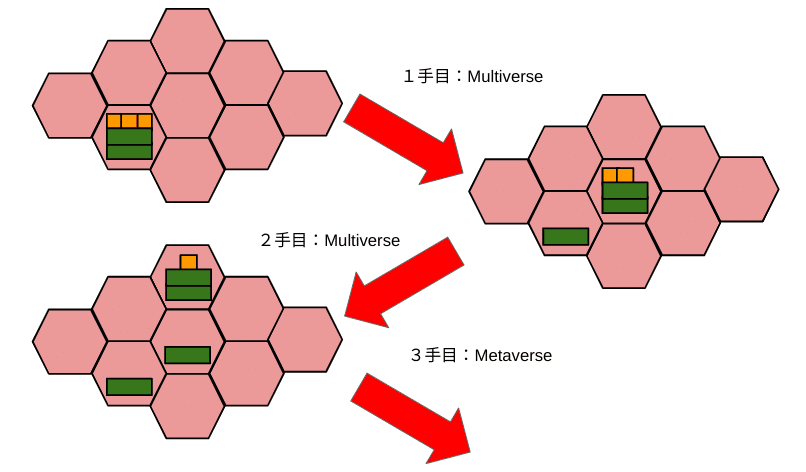

(ネビュラ1個とメタ2個のスタックが正しい)

(ネビュラ1個とメタ3個のスタックが正しい)
