【岐阜県公立高校入試】数学　図形の証明問題　出題傾向　過去39年

岐阜県公立高校入試の数学では、毎年必ず図形の証明問題が出題されています。

今回は昭和60年度から令和5年度までの39年間における出題傾向をまとめてみました。

受験生のみなさんの参考になれば幸いです。

【昭和60〜63年度】

昭和60年度　三角形の合同　円周角を利用
昭和61年度　ひし形の証明　正五角形の辺と対角線
昭和62年度　平行四辺形の証明　中点連結定理
昭和63年度　4点同一円周上の証明　円周角の定理の逆

【平成元〜10年度】

平成元年度　線分の中点である証明　中点連結定理
平成2年度　三角形の相似　同心2円と三平方の定理
平成3年度　辺の長さが等しい　垂直二等分線
平成4年度　三角形の合同　円に内接する四角形の定理
平成5年度　円周角の定理　定理そのものの証明

平成6年度　三角形の合同　（90°−同一角）の利用
平成7年度　三角形の相似　接線と弦の定理
平成8年度　辺の長さが等しい　折り返し図形の辺と角
平成9年度　辺の長さが等しい　中点連結定理
平成10年度　4点同一円周上の証明　三角形の合同と円周角の定理の逆

【平成11〜20年度】

平成11年度　角の大きさが等しい　折り返し図形の角
平成12年度　角の大きさが等しい　円周角と接線、（90°−同一角）
平成13年度　三角形の相似　2組の辺の比
平成14年度　辺の長さが等しい　三角形の合同
平成15年度　三角形の相似　ひし形を示して同位角

平成16年度　辺の長さが等しい　三角形の合同、正方形ずらし
平成17年度　三角形の相似（空欄補充）&三角形の合同　円周角、一辺両端角相等
平成18年度　三角形の相似　長方形折り返し、（90°−同一角）
平成19年度　平行四辺形の証明　三角形の合同を利用
平成20年度　三角形の合同　直角二等辺三角形ずらし、（90°＋同一角）

【平成21〜31年度】

平成21年度　三角形の相似　円周角
平成22年度　三角形の合同　平行四辺形
平成23年度　三角形の相似　長方形ずらし、（90°−同一角）
平成24年度　三角形の合同　中点連結定理
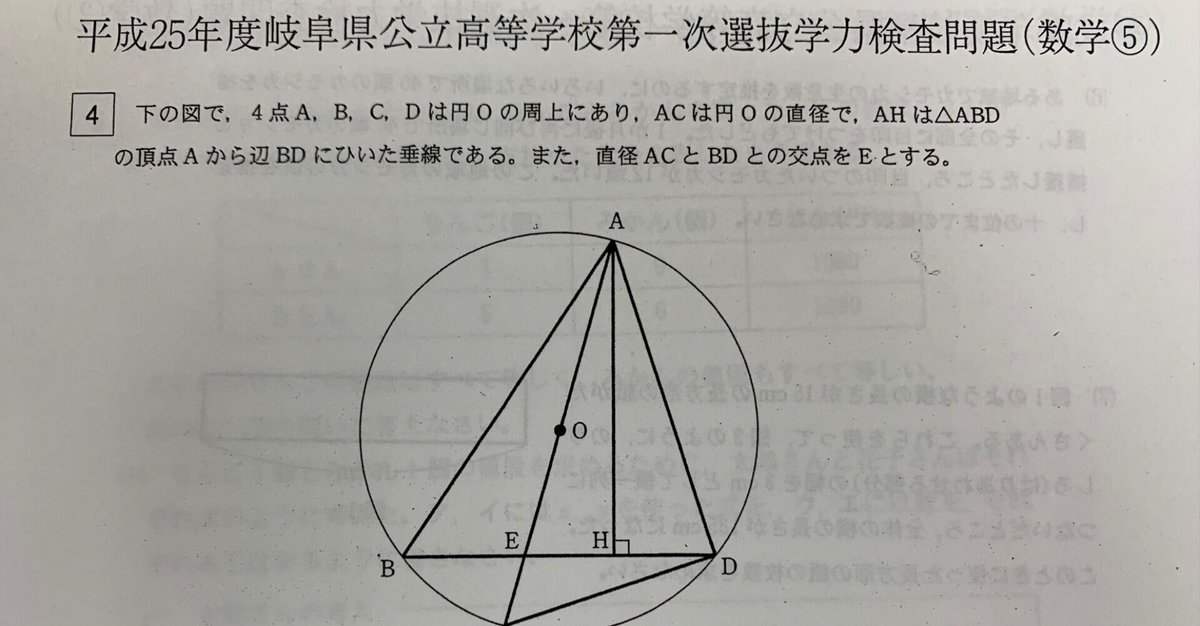
平成25年度　三角形の相似　円周角、直径

平成26年度　三角形の合同　2つの異なる正方形ずらし、（90°−同一角）
平成27年度　三角形の相似　辺の比（長さあり）
平成28年度　三角形の合同　円周角、直径
平成29年度　三角形の相似　長方形折り返し
平成30年度　三角形の合同　2つの異なる正三角形ずらし、（60°＋同一角）

平成31年度　三角形の相似　円周角、平行線の錯角

【令和2〜5年度】

令和2年度　三角形の合同　2つの異なる直角二等辺三角形ずらし、（90°−同一角）
令和3年度　辺の長さが等しい　円と正三角形、三角形の合同を利用
令和4年度　三角形の相似　角の二等分線と辺との交点（BA:BC=AD:CDの利用）
令和5年度　三角形の相似　円周角の定理、平行線の錯角

【まとめ】

昭和末期から平成前半にかけては、辺の長さや角の大きさ、ひし形や平行四辺形の証明、4点同一円周上の証明などバラエティに富んでおり、三角形の合同や相似そのものの証明は20年間で5回にとどまっている。

一方で、平成後半からは、三角形の合同や相似そのものの証明の出題が大半となり、特に、平成20年度以降、令和2年度まで13年連続で合同と相似の証明が交互に出題された。

令和3年度に、平成16年度以来17年ぶりに辺の長さが等しいことを証明する問題が出題されたが、こちらの証明は三角形の合同を利用するものであった。令和2年度が三角形の合同の出題だったことから、合同と相似が交互に出題されてきた傾向からも外れたことになる。令和4年度、令和5年度は連続して三角形の相似を証明する問題が出題された。相似の証明が連続して出題されるのは、平成12年度、13年度以来のことだった。

受験生諸君は「ヤマ張り」などせずに、広く学習に取り組んでほしい。特に証明は10点問題なので、確実に得点できるようにしてほしい、⑵のイが例年難問なため、最難関を受験する場合でも、即答が困難なら、捨てて次へ向かう方が賢明だろう。特に、平成25年度や平成30年度レベルの問題が出た場合、取捨選択の判断をできるのも実力だと言えよう。

すべての受験生のみなさん、最後まで準備を怠らず、できる限りの全力で取り組んでほしい