
1分で解ける?令和3年度 岡山高等学校入試問題ー図形ー
令和3年度 岡山高等学校入試の問題です。

右の図の円 O について,∠𝑥 の大きさを求めなさい。 ただし,AB は直径である。
定理で解く
この問題はタレスの定理を使って解きます。円の直径に対する円周角は直角です(タレスの定理)。
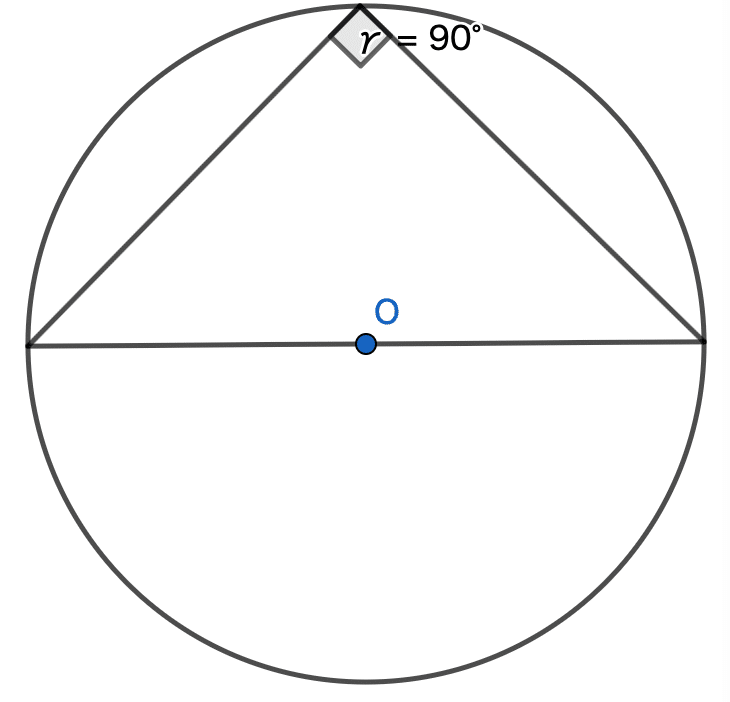
タレスの定理から,角 ACB は直角,90°です。αは 80°ですから,α以外の角度は 90° - 80°で 10°です。
弧が同じであれば,円周角の大きさも同じになります。ですから,x は 10°。答えは10°です。
タレスの定理
円の直径に対する円周角は、直角
円の直径というのは,次の赤い線分のことをいいます。

円周角は,円の周りにある角のことをいいます。この角の角度が直角,90°というのがタレスの定理です。

タレスの定理の証明
【図4】のように補助線を引きます。二つの三角形ができます。いずれも二等辺三角形です。二辺が円の直径だからです。
二等辺三角形ですので,ふたつの底角は同じ大きさになります。底角というのは頂角以外のふたつの角のことです。頂角とは同じ長さの二つの線分にはさまれてできた角度のことです。

簡単のために,丸印で示した角を a,バツ印で示した角を b としましょう。
三角形の内角の和は180°ですから,次のように書くことができます。
$$
a + a + b + b = 180 \\
2a + 2b = 180 \\
a + b = 90
$$
$${a+b=90}$$ ということは,丸印の角度とバツ印の角度を足すと90°,直角になるということです。これでタレスの定理が成り立つことがわかりました。
タレスの定理は,円周角の定理から導かれます。円周角の定理については別のところで触れたいと思っています。
