
中学の数学 文を式に (3) マイナスとマイナスでプラスになるのはなぜ?
今日の目的
マイナスで数の何を操作しているのか理解できる
理解度の確認
$${2-(-3)}$$ を計算できる
前回の復習
前回,マイナスは「戻る」操作だと勉強しました。
次の式をみてください。
$${2-3}$$
$${2}$$ というは,正負の記号をつけたら,$${+2}$$ です。
プラスというのは,数直線でいうと右の方向を見ているということです。図でいうと以下のようになります。画像は「ドット絵ダウンロードサイト DOTOWN」(https://dotown.maeda-design-room.net) のものです。

$${-}$$ は「戻る」ということです。戻るとは,数直線でいうと,次のようなことです。右の方向を見ていたひとが左の方向を向くことです。

そして,次に$${3}$$ とあります。そのまま $${3}$$ 進みます。

すると,今経っているのは $${-1}$$ の位置です。$${2-3}$$の答えは,$${-1}$$です。
2-(-3) はどう考える?
$${2-(-3)}$$ はどうなるのでしょう。
ひとつひとつ見ていきましょう。
$${2}$$。まず,数直線のうえで右の方をむいてひとが立っています。
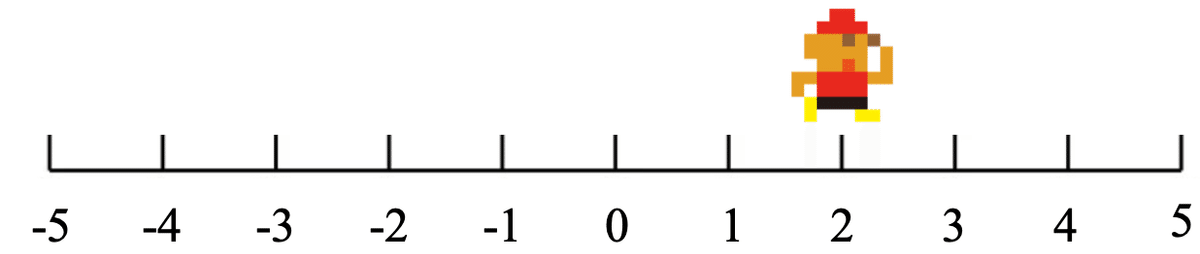
$${-}$$。左の方に向きを変えます。

$${(-3)}$$。まず$${-}$$があるので,再び,右の方に向きを変えます。

$${3}$$。そして3つ進みます。どこにいますか。
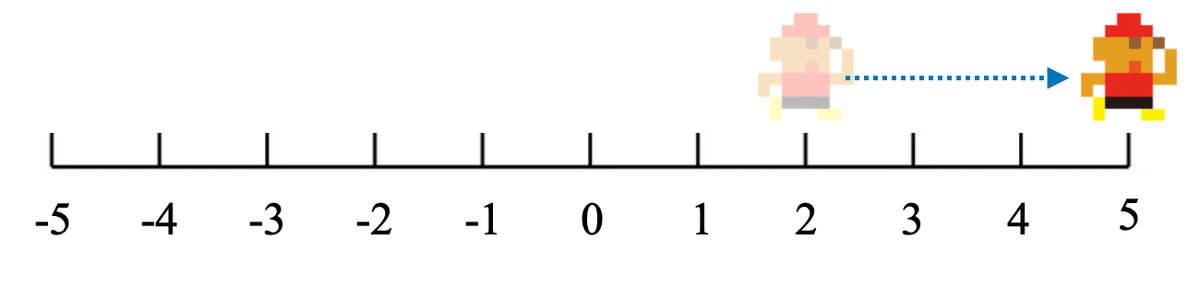
そうです。5 の位置にいます。
マイナスが続くとプラスになる
$${2-(-3)}$$ のようにマイナスが2個続くとプラスになります。なぜ?と思うひとも多いと思かったでしょう。
今日の勉強で理解できたのではないでしょうか。
マイナスは「戻る」,つまり,くるりと向きを変えることです。くるりと向きをかえて,また,くるりと向きを変えたら,最初と同じプラスの方向をみていますね。
ですから,マイナスが2個続くとプラスになります。
練習
こんな計算をする必要はありませんが,練習のためしてみましょう。
問題 1 $${1-2}$$
問題 2 $${1-(-2)}$$
問題 3 $${1-(-(-2))}$$
問題 4 $${1-(-(-(-2)))}$$
解説
問題 1 $${1-2}$$はそのまま$${1-2=-1}$$。
問題 2 $${1-(-2)}$$は$${1+2}$$に直せます。$${1+2=3}$$。
問題 3 $${1-(-(-2))}$$は$${1-2}$$に直せます。$${1-2=-1}$$。
問題 4 $${1-(-(-(-2)))}$$は$${1+2}$$に直せます。$${1+2=3}$$。
おすすめの書籍
マイナスとマイナスが続くと,プラスとする。
なぜ?
先生に聞くと,そういうふうに覚えなさいと言われるかもしれません。
なぜ先生がそういうふうにいうのでしょう。
ひとつは面倒だから,もうひとつはひとつひとつを丁寧にしていると前に進めないからです。
しかし,世の中には理屈がわからないと絶対に前に進めないひともいます。そのひとは確かに進む速さはかなり遅いでしょう。
しかし,もしかすると,何年後には数学が得意になり,数学を使って将来仕事をしているかもしれません,仕事で使うまでになるには,やはり意味がわかってないと難しいです。
ちょっとくらい理解が遅いと思っていても気にしなくてもよいでしょう。先生のいうように暗記しておこうと自分で考えない限り,そのうち数学って何をしているのかわからなくなると思います。たぶん応用問題を解くのは難しいんじゃないかな。
大人になって考える力がついてから,学び直すとよくわかるということはよくあります。
