色を科学する　その⑤ 色はベクトルー＞

　RGBやXYZといった三刺激値は、グラスマンの法則にあるように、加法則や比例則が成り立つので、線形代数学の対象として扱うことができ、色は、RGBまたはXYZといった原刺激を空間の軸（基底）とした3次元空間内のベクトルとして表現できます。

等色関数をベクトルで表すと

　「色を科学する　その②」でも書きましたが、等色関数は別名「スペクトル三刺激値」、つまり、単色光（スぺクトル）をマッチングするのに必要な三原色の量です。XYZ表色系ならば、三刺激値と呼ばれる（X, Y, Z）という3つの数で色を表現します。

　そこでXYZという原刺激が”張る"（空間の軸となる）空間において、各単色光の（X, Y, Z）＝等色関数をベクトルとして表現すると↓のようになります。見慣れた「波長に対する折れ線グラフ」とは、全然見え方変わりますね。

全ての色はベクトルである

　単色光以外の任意の色（Cとします）も同様にこの空間内のベクトルとして表現でき、ベクトルの方向、すなわち（Xc, Yc, Zc）の比率が色み（色相と彩度）を表し、長さが明るさを、、、といたいところですが、XYZ表色系では、Yに明るさ情報をすべて詰め込んでいるので、高さが明るさを表します（RGB表色系では「長さが明るさ」といえます）。

　なので、Y=0であるXZ平面上の色はすべて明るさが0です（その下は明るさがマイナス！）。そんな色は存在しない（虚色）なのですが、440nmあたりの青の単色光はこの面スレスレのベクトルとしてぐいっと伸びています。つまり、明るさはほぼ0なんだけど、色みとしては強い、ちょっと不思議な色です。RGB表色系の輝度の計算式において、435.8nmの単色光であるBの係数が0.0601と異常に小さいのもこのためです。

等色関数のマイナスをベクトルで表現

　ここで、すべての単色光のベクトルは、X、Y、Zがすべて手前側の正の領域にあることがわかると思います。これは、等色関数にマイナス(負)の部分ががないためです。

　一方RGB表色系の等色関数をRGBの空間に描くと、↓のようになり、440nm～540nmのベクトルが、大きく後ろに反り返っており、Rがマイナスになっています。

加法混色はベクトル合成

　ベクトルといえば、ベクトル合成の図が思い浮かびます。

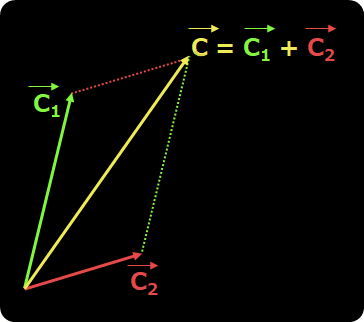
　色(光)もこのような合成ができます、それが加法混色です。色C1と色C2を合成＝加法混色し、色Cとなったことをベクトル合成で表すと↓のようになります。加法混色なので、色Cの輝度Ycは、C1とC2の輝度の和（Yc1+Yc2）になります。

　そもそも、下図↓のように色Cは色Xc、Yc、Zcの合成＝加法混色結果でもあります。

　次はいよいよ「色度図」に触れたいと思います！