早慶には「附属校プレミアム」が存在するが、MARCHには存在しない ※修正中
駿台全国模試の判定偏差値の設定基準を私が勘違いしていたことがわかりました。現在、過去の分析を再分析中です。以下の記事内容は今後修正の予定です。修正前の記事としてご覧下さい。(2024.10.12)
私が愛読しているイブリースさんの記事で、「偏差値キルヒホッフの法則」という概念が提唱されています。具体的には以下のように定義されています。
こう考えると、新たな原理が思い浮かぶ。それは「どのルートで入学したとしても、得られる学歴が同等であれば、そこまで乗り越えるべき関門は変わらない」という原理だ。偏差値の高い学校というのは例えるならば水位が高いような状態であり、そこまで至る過程の標高差は変わらないということだ。まるで物理学の保存力とか、キルヒホッフの法則のようである。
なかなか興味深い法則です。この法則が成立するなら、早慶MARCHの大学に入学するには、中学受験や高校受験で附属校に進学するのも、大学受験で勝負するのも同じ難易度ということになります。そこで、今回はこの法則が成立するのかを定量分析してみます。なお、今回もデータの取得時期が一致していませんので、分析結果の数値は厳密なものではなく、概算として捉えて下さい。
0. まとめ
早慶本命率、難関大学進学率から分析すると、早慶の大学合格では「偏差値キルヒホッフの法則」は成立しない。
早慶入学は大学受験よりも中学受験・高校受験の方が難易度が高く、早慶の附属中高の合格には「附属校プレミアム」が必要となる(偏差値で+2相当)。
一方、MARCHの大学合格に関しては、中学受験/高校受験/大学受験で難易度はほぼ同等であり、「偏差値キルヒホッフ」の法則が成立している。逆に言えば、MARCHの「附属校プレミアム」はゼロである。
1. 早慶MARCHの合格難易度
①大学受験の難易度
一般入試を対象として、駿台全国模試の偏差値を比較指標として採用します。前回の記事で作成した表(早慶のみ)にMARCHを加えると、表1になります。私立高校の受験との比較のため、3科目・文理差なしの補正を入れています。MARCHのA判定推定は、B判定+3で行っています。その他の補正ロジックは早慶と同じです。合格者平均は過去の分析の結果から、B判定偏差値−3としています。
計算の結果、大学入試の難易度は、駿台全国模試の偏差値(3科目・文理補正後)で、早慶の合格者平均は56.2、MARCH平均は47.9となりました。

②高校受験の難易度
一般入試を対象として、駿台中学生テストの偏差値を比較指標として採用します。可能圏(60%)と確実圏(80%)の判定偏差値(2022年冬調査)を集計すると、表2となります。合格者平均については、高校別の合否偏差値分布を掲載していたブログがあり、それを眺めると、概算で合格者平均=確実圏−6/可能圏−2でした。今回は双方の平均値を合格者平均として採用しています。
計算の結果、高校入試の難易度は、駿台中学生テストの偏差値(3科目)で、早慶の合格者平均は59.4、MARCH平均は49.1となりました。

③中学受験の難易度
志望校判定サピックスオープン(以下、SAPIX)の偏差値を比較指標として採用します。80%偏差値は2024年4月の数字です。合格者平均については、開成と桜蔭の合否偏差値分布のグラフを掲載しているブログがあったので、その分布のピークを見て80%偏差値−2で計算しています。
計算の結果、中学入試の難易度は、SAPIXの偏差値で、早慶の合格者平均は57.4、MARCH平均は47.1となりました。

2. 模試間の偏差値の比較
本来なら上記で分析に用いた3つの模試は、受験時期も母集団も違うので同列で比較できません。ただ、3つの模試の母集団の学力レベルが同等なら、その同等な母集団内の相対分布を示す偏差値は同じになるはずなので、3つの模試の偏差値の変換モデルは構築可能です。
この考え方で、3つの模試の間でに偏差値変換モデルを前回に検討しました。導出された変換式は「駿台全国模試の偏差値≒駿台中学生テストの偏差値≒志望校判定SAPIXオープンの偏差値+α(αは0〜1)」となりました。このうち、SAPIXにつくαは誤差として、0の場合と1の場合の2種類で計算します。
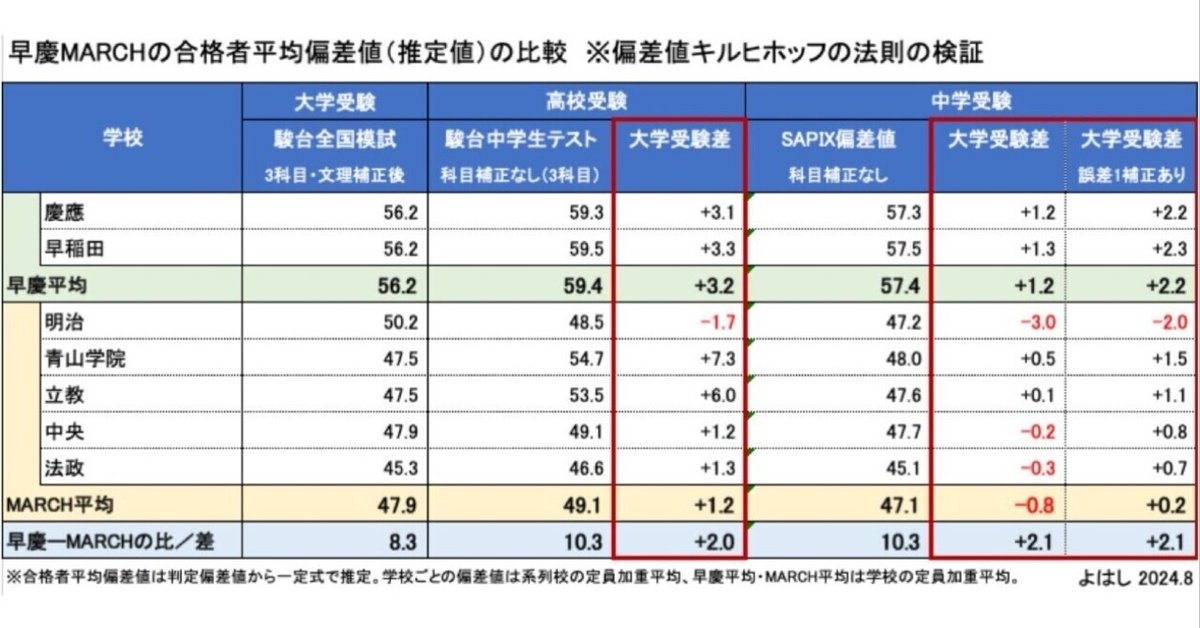
この変換式を用いて、大学受験、高校受験、中学受験の早慶MARCHの合格者平均を比較すると表4となります。

例えば、慶應大の合格者の駿台全国模試の平均偏差値は一番左上の56.2です。慶應附属高校の合格者の駿台中学生テストの平均偏差値はその隣の59.3となります。先の変換式では駿台全国模試=駿台中学生テストであり、それぞれの偏差値は同列で扱えるので、単純に差を取ると、慶應附属高校の合格者は慶應大合格者よりも平均偏差値で3.1高いことがわかります。
一方、中学との対比でも、駿台全国模試≒SAPIXです。同様に単純に差を取ると、慶應附属中学の合格者は慶應大合格者よりも平均偏差値で1.2高いことがわかります。誤差1を加味(駿台全国模試≒SAPIX+1)するなら、差は+2.2となります。
この計算を早慶MARCHの大学それぞれに実施し、早慶とMARCHでそれぞれ定員加重平均を取ると、早慶平均がグリーン列、MARCH平均がイエロー列となります。早慶とMARCHの格差が一番したのブルー列です。
3. 偏差値キルヒホッフの法則の検証
それでは表4の数字を見ながら、偏差値キルヒホッフの法則を検証していきます。
①早慶
高校受験の早慶附属の難易度は、大学受験の早慶の難易度よりも偏差値で+3.2も高いです。中学受験でも+1.2〜2.2となっています。中高を平均すると、+2.2〜2.7です。偏差値が4〜5違うと学校のランクが1つ変わるので、偏差値2.2〜2.7の差は0.5ランクぐらいの差があります。これは大学受験だと早慶と上智・東京理科大・ICUくらいの差です。
感覚的ではありますが、0.5ランクの差があると、早慶の大学の難易度と附属中高の難易度は同等とは判断しづらく、偏差値キルヒホッフの法則は早慶では成立しないと言わざる得ません。
逆に言えば、附属中高に出る偏差値+2.2〜2.7(0.5ランク)のアップ分は、早慶の大学への入学を先に確保するための権利見合いが附属中高の合格には必要となっている、とも言えます。ファイナンスの世界では、買収時の将来利益の伸びの期待値を株価に上乗せする分をプレミアムと呼ぶので、それに習って、この附属中高側に出る偏差値の差分を「附属校プレミアム」と呼ぶことにします。
②MARCH
高校受験の早慶附属の難易度は、大学受験の早慶の難易度よりも偏差値で+1.2あります。一方、中学受験では-0.8〜+0.2とほぼゼロです。中高平均で+0.2〜0.7とわずかな数字です。これくらいの差なら、MARCHでは大学の合格者平均と附属中高の合格者平均は等しいとしても問題ないと考えます。つまり、MARCHでは偏差値キルヒホッフの法則が成立し、附属校プレミアムはゼロである、と言えます。
この場合、MARCHの附属校プレミアムがゼロなのは悪いことではないです。MARCHの附属校合格者は、余計な追加コストを支払わずに、MARCHの大学受験を回避して入学する権利を入手したと解釈できます。その意味では、MARCHの附属校合格はコストパフォーマンスが高いと言えます。
③早慶ーMARCH差
一番下のブルーの列が、それぞれの受験での早慶とMARCHの合格者平均偏差値の差です。大学受験では8.3の差があるのが、高校受験と中学受験では10.3の差に拡大しています。これは、MARCHの附属校プレミアムがゼロなのに対し、早慶には+2.2〜2.7の附属校プレミアムが存在するため、その分が拡大していると解釈できます。
このことは時系列で考えれば、中学受験で早慶附属校に合格した際に支払う附属校プレミアム(偏差値2相当)は、高校にエスカレーターで進学した際にも留保され、大学受験時に権利行使の対価として解消されると理解できます。高校受験で早慶附属校に合格した場合でも、同等の附属校プレミアムを支払うことになります。早慶の附属校プレミアムは大学受験回避の価値の先払いなので、中学受験でも高校受験でも等価で偏差値+2相当と考えるのが妥当です。
4. 最後に
イブリースさんの理論はこれまでも検証分析を行ってきましたが、これまでは理論を肯定する結果が裏付けする結果が出ていました。今回の偏差値キルヒホッフの法則は、MARCHでは大学と附属校の間で成立したのですが、残念ながら早慶では成立しませんでした。むしろ、早慶の附属校の合格には「附属校プレミアム(偏差値+2相当)」が必要というのが考察結果です。
イブリースさんは東大進学率10〜20%の進学校を基準にして、偏差値キルヒホッフの法則を導出されていたので、大学での早慶合格ではセグメントの違いが出ている可能性があります。この辺りは、もう一段の分析を行いたいところです。
また、附属校プレミアムは早慶では確認できたのに、MARCHではほぼ確認できなかった理由も解き明かせていません。これも興味がある分析対象です。
そもそもの、模試間の偏差値変換が正しいのかという前提の疑問はありますが、今回の分析はここまでとします。
