
早慶本命率の推定の誤差(残差)についての分析
noteに投稿していた記事を、X連携機能を試しに使ってXにポストしてみたところ、1ヶ月以上も音沙汰なかったのですが、最近になってリポストしてくれる人が初めて出ました。感謝です。
リポスト先では、統計用語の私の記憶違い(恥ずかしい限りです)や分析内容についてのコメントをもらいました。そのコメントの中に、複数の推定を組み合わせた結論は誤差が拡大しているのではないか、という指摘がありました。確かにその通りです。
これまでの分析は私の納得が得られるレベルの精度があれば十分と考えて、精度を上げること、つまり残差の評価は目を瞑ってました。ただ、思い返せば、大学時代に社会科学系で統計学を実習する授業(計量経済学とか地域分析とか)では、残差の評価をかなりやった記憶があります。
そこで、考えを改めて、たまには残差の評価もやってみます。残差の評価対象は直近で回帰分析を行なった早慶本命率と難関大学進学率の推定です。まず今回は早慶本命率の推定の残債の分析を行います。
1. 早慶本命率の回帰分析結果
過去に導出した早慶本命率の1次回帰式はこのようになります。本命率=進学者÷合格者です。これらの回帰式からの予測値と実測値の残差を見ていきます。なお、以降で扱うのはいずれも現役のデータなので、推定値は正しくは現役本命率となります。
【高校受験モデル】高校の大学受験時の早慶本命率=-0.0161 × 駿台中学生テスト確実圏偏差値 + 1.3419(決定係数:0.5070)
【中学受験モデル】中学の大学受験時の早慶本命率=-0.0124× 駿台中学生テスト確実圏偏差値 + 1.0554(決定係数:0.4468)
前回分析時のデータにいくつか転記ミスが見つかりました。以降は修正後のデータで再計算しています。なお、全体に与える影響は軽微のため、元記事は後日修正します。
2. 回帰式の残差の分析
①高校受験モデルの残差
高校受験モデルの対象46校について、回帰式からの早慶本命率の推定値と実際の本命率との残差は、この表のようになります。標本の選定背景は、上記の前回記事をご参照ください。後述する残差の異常値にはオレンジ色をつけています。

この残差の分布をグラフにすると、このようになります。上が横軸を確実圏偏差値にしたグラフで、下が横軸を早慶本命率(実値)にしたグラフです。

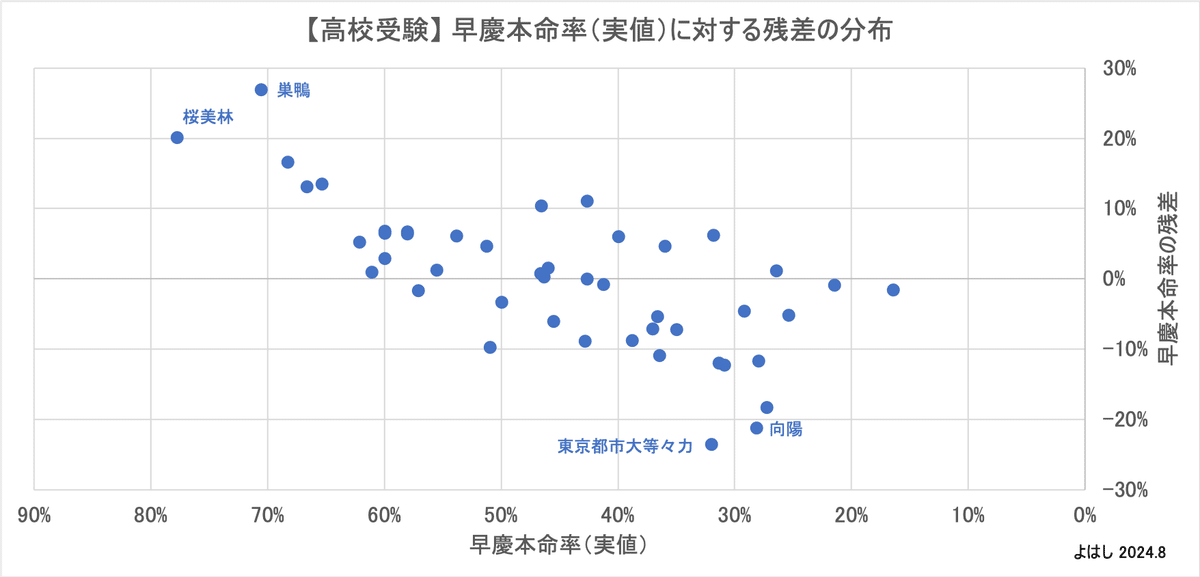
どちらのグラフも概ね早慶本命率0%前後に分布していますが、いくつか異常値が見られます。高校の名前を見ても、異常値が出た理由は思い当たりません。
ヒストグラムにすると、こんな感じです(グラフ3)。上下の異常値が多少歪みを作っていますが、中央は正規分布に近い分布イメージです。

四分位点を計算すると、第一四分位点が▲6.8%、中央値が0.6%、第三四分位点が+6.2%でした。残差の中央値は理論値のゼロにかなり近い値であり、2つの四分位点がほぼ上下対称であることが確認できます。
②中学受験モデルの残差
中学受験は過去の分析の蓄積がないので、データ数は少ないです。22件なので、統計分析のデータ数としては少ないですが、趣味のレベルなのでこれで分析しています。
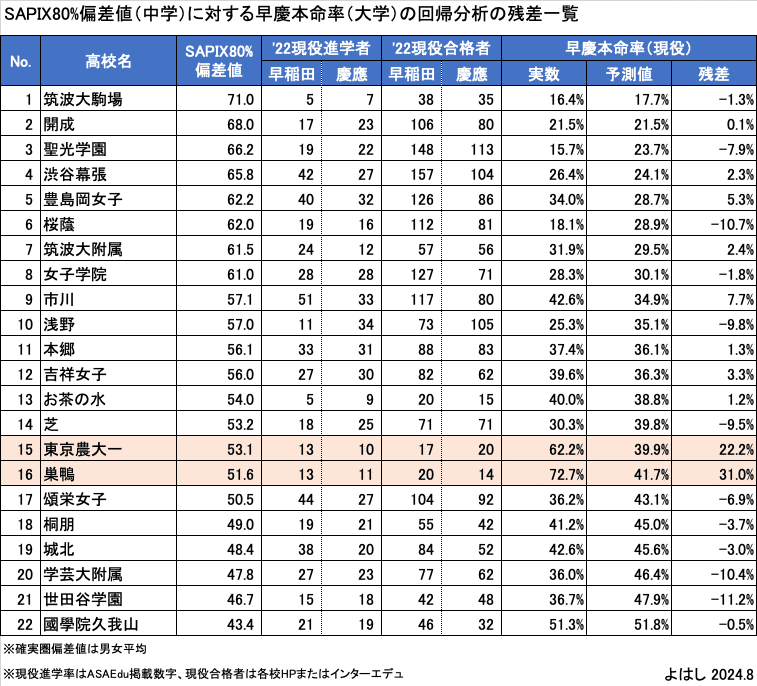
高校の分析と同じようにグラフにすると、このようになります。



こちらも異常値が目立ちます。巣鴨と東京農大一です。東京農大一は受験科目が少ないようで、それがSAPIX偏差値を押し上げている可能性はありますが、それにしても残差が20%超となるのは不可解です。巣鴨は相変わらず理由はわかりません。
ただ、ヒストグラム(グラフ6)を見ると、20%以上の2つを除くと、残差は±10%に入っています。四分位点を計算すると、第一四分位点が▲7.7%、中央値が0.9%、第三四分位点が+2.3%でした。残差の中央値は理論値のゼロにかなり近い値ですが、分布は正規分布ではなさそうです。正規分布にならない理由が何かあるのかもしれませんが、データ数が少ないことに起因している可能性もあります。
3. 残差の評価
高校受験モデルも中学受験モデルも異常値は見られました。異常値を除いて決定係数を計算すると、高校モデルは0.5070から0.6492に上昇し、中学モデルは0.4468から0.6700に上昇します。本来なら異常値を除いて回帰分析する方が良かったかもしれません。
ただ、ヒストグラムや四分位点を見ると、どちらも本命率の残差は±10%に治まっています。早慶本命率の標本平均は高校受験モデルで45%、中学受験モデルで33%でした。ここから±10%ズレるとすると、残差の相対量は±0.22〜0.30です。
この早慶本命率は難関大学進学者を推定する際に用います。前回記事で分析した早慶進学者数の定員比は標本平均で18.5%です。これに対する残差が相対量で±0.22〜0.30ズレる可能性があるなら、早慶本命率の誤差は難関大学進学率に対して±3〜5%程度の誤差を生む可能性があります。
前回の分析対象の高校の難関大学進学率は20〜80%くらいに分布していました。この誤差の規模(±3〜5%/20〜80%)は、高校によってはインパクト大きいかもしれません。もう少し精度に拘って、回帰分析した後に残差分析もちゃんとやっておくべきだったと、少し反省です。
4. 最後に
今回の残差分析にあたり、統計のテキストを読むと、真の回帰モデルの導出が次にやることでした。たぶん、学生時代には余裕で理解していたはずです。ただ、今となると、何のことやら直感的にわかりません。
また、誤差と残差の用語の使い分けは正しくできているか自信ないです。大学時代には理解していたはずなのですが。
どうもこれ以上の深掘りはできそうにないです。
そのため、早慶本命率の誤差(残差)の分析は一旦ここまでとして、次回は難関大学進学率の誤差(残差)をもう一段分析してみます
