
異なる模試の偏差値比較(変換)に関する考察
一般論としては、模試が異なれば母集団が違うので、異なる模試の間では偏差値の比較はできません。ただ、受験生をもつ親としては、子供が違う模試を受験した場合、それぞれの成績表を見て、成績が上がっているのか下がっているのか比較したくなります。そのため、これまでの記事で、異なる模試の偏差値比較(変換)について、いくつか分析してきました。
そうした中、先日にこちらのブログを読んだ際に、「鉄緑会プレミアムを計算できるかも」と思いつきました。
ただ、そのためには異なる模試の偏差値比較(変換)が必要になります。そこで、鉄緑会プレミアムの計算の前に、異なる模試の偏差値の比較は可能なのかどうかの考察を、改めて整理してみます。ちょっと長文です。
1. 筆者の見解
基本的には異なる模試の偏差値の比較や変換はできない。
ただし、同じ受験年度の同じ学年の模試(例:大学受験の駿台全国模試と全統記述模試)であれば、受験生全体の母集団は同じであり、模試によって標本が違うだけなので、異なる模試の偏差値の比較や変換は理論的には可能。ただし、個々の大学・学部・学科ごとの比較には、誤差(残差)が存在する。
一方、異なる受験年度の異なる学年の模試(例:中学受験のSAPIXオープンと高校受験の駿台中学生テスト)は、受験生全体の母集団が異なるので、上記ののロジックは適用できない。しかし、異なる受験年度の異なる学年の模試でも、同一の学力となる標本を定義して、その標本がそれぞれの模試を受験したと仮定することで、異なる模試の偏差値の比較・変換は推定レベルでは可能。
2. 模試間の偏差値を単純比較できない理由
異なる模試の偏差値を比較できない理由については、「母集団が違うため」というのが一般論です。それでは、母集団が違うと何が違うでしょうか? 本当に母集団の違いだけが理由なのでしょうか? まずは、この点を掘り下げて検討してみます。
①判定基準の違い
模試間の偏差値比較についてのブログや掲示板で、実はあまり触れられないのがこの点です。模試によって、合格者平均偏差値に対する合格可能性80%の位置が異なります。
例えば、中学受験の合格力判定SAPIXオープンだと、図1に引用したグラフのように、東邦大学附属東邦中学校の合格可能生80%のラインは、合格者の分布のピーク(中央値)付近に設定されています。
(出典)https://www.sapientica.com/application/mockexam/04/img-map/11.html

ブログを探すと他の中学の合否分布も見つけられました。SAPIXオープンではなく、四谷大塚合不合テストではありますが、開成中学や桜蔭中学では合格者ピーク+1〜2に合格可能生80%ラインがあるようです。
一方、駿台中学生テストでは、公式には合否分布データのサンプルは出ていませんが、過去に出回ったものが、今でもブログや掲示板に少し残っています。それらを見ると、確実圏偏差値(合格可能生80%)からマイナス6〜7くらいに合格者の偏差値のピークがある高校が多いようでした。
さらに、大学受験の模試も見てみます。
駿台全国模試の難関国立大の合格者平均偏差値が、次のホームページで公式に公開されています。ここにある数字を駿台全国模試の合格目標ライン偏差値(合格可能性80%)を比較して、その差の定員加重平均をとると、合格者平均偏差値は目標ライン偏差値マイナス4くらいにあることがわかります。
また、河合塾の全統記述模試についても、いくつかの大学の合格者平均偏差値が掲示板に出ていたことがあります。そこに掲載されていた数字からいくつか計算すると、合格者平均偏差値は、東大ではA判定偏差値マイナス1〜2、一橋大・東工大・東京医歯大(医医)ではA判定マイナス4〜5くらいでした。全体平均すると、難関大学の合格者平均偏差値はA判定偏差値マイナス3〜4ではないかと思われます。
これらについて、式の左右を入れ替えて一覧で整理すると、このようになります。
SAPIXオープンの合格可能性80%ライン=合格者平均偏差値+1〜2
駿台中学生テストの合格可能性80%ライン=合格者平均偏差値+6〜7
駿台全国模試の合格可能性80%ライン=合格者平均偏差値+4
河合塾全統記述模試の合格可能性80%ライン=合格者平均偏差値+3〜4
このように、合格者平均偏差値と合格可能性80%偏差値の位置づけが異なります。つまり、模試の間で合格可能性の判定偏差値で、どちらの模試が上か下かを比較することは意味がありません。同様に、判定偏差値で、模試受験者の母集団の違いを比較することはミスリードすることになります。
なお、この差が生じる理由は、合不合の補足率の違い(不合格の補足率が低いと実態より合格率は高く出る)などが考えられますが、解明には至っていません。
②総合偏差値の計算方法の違い
3教科偏差値や5教科偏差値の計算方法は、模試によって異なります。大学受験で見ると、駿台全国模試は3教科の合計点の偏差値なのに対して、全統記述模試は3教科の偏差値の平均値を採用しているようです。そのため、全ての科目の偏差値が同一でも、全統記述模試の偏差値の方が駿台全国模試よりも総合偏差値は小さくなります。
③時間軸の違い
当たり前ですが、中学受験と高校受験では受験者が重なることはあっても、受験者母集団が一致することはありません。高校受験と大学受験でも受験者母集団は当然異なります。
また、同じ模試でも受験学年が異なると受験生母集団が異なります。例えば、大学受験模試では、高3になると浪人生も受験するため、母集団の学力レベルは上がります。そのため、同じ学力で同じ模試を受験しても、高1〜2の時の偏差値より高3の偏差値は低く出るはずです。
他にも、同じ学年で開催回が違う場合には、塾や学校の単位での一斉受験による構成差が母集団の学力レベルに影響します。ただし、同一学年の同じ模試であれば、開催回が違っても母集団の差は軽微と考えられるので、開催回の差については以下では無視します。
④受験者の学力レベルの違い
ネットで注目されるのはこの点ですが、上記①〜③のような構造的な差異要因がある上で、最後にこの差が出ます。いわゆる、SAPIXオープンは四谷大塚合不合テストよりも受験生の学力レベルが高く、偏差値は低く出るという話です。
それぞれの模試は受験者の学力レベルを想定して、問題の難易度を決めていると考えられます。逆に考えると、それぞれの模試の模試の難易度に応じて、受験者母集団の学力レベルに違いが出ます。その結果として、同じ学力でも模試によって偏差値に違いが出ることになります。
更に、大学受験の大学・学部・学科の判定偏差値は、文系・理系の学力差、国立受験者(4〜5科目)・私立受験者(2〜4科目)の学力差の影響も受けます。これまでの分析から、文系の偏差値=理系の偏差値+2程度、私立大学(3教科)=国立大学(4教科)+1くらいの補正が必要と考えています。
なお、長期的には、同年齢の人口や大学進学率が模試の母集団に影響も受けます。私が大学受験した30年前と現在を比較すると、大学進学率が上がって、全統記述模試の受験者数は増えています。この場合、全統記述模試の受験者の学力レベルは、30年前よりも低下していることになります。ただし、長期比較では学力レベルのマクロ変動を考慮が必要ですが、今回は短期の比較なので、この点は無視することにします。
3. 異なる模試の偏差値を比較・変換のロジック
上記のような4つの要因で模試間で偏差値の違いが出るのであれば、これらの要因を解消するロジックを入れたら、模試間の偏差値の比較や変換ができるはずです。別の言い方をすると、模試の判定偏差値を直接の比較はできなくても、同等の学力の受験者グループ(標本)の模試ごとの偏差値がわかれば、異なる模試の偏差値を間接的に比較・変換できると言えます。
このような考え方で、2つのパターンで、異なる模試の偏差値の比較・変換のロジックを整理してみます。
◆同じ受験生母集団における異なる模試受験者の標本の比較
中学受験のSAPIXオープンと四谷大塚合不合テスト、大学受験の駿台全国模試と河合塾・全統記述模試のように、入試年度が同じ受験生(20XX年の中学受験/大学受験)における異なる模試の比較がこのパターンです。
このパターンでは、受験生全体を母集団とすると、それぞれの模試の受験者はこの母集団の標本という位置づけとなります。同様に、特定の学校の受験生もこの母集団の標本となります。そして、模試受験者の標本と特定の学校の受験生の標本は重なります。大学受験での東大受験を例にすると、このようになります。
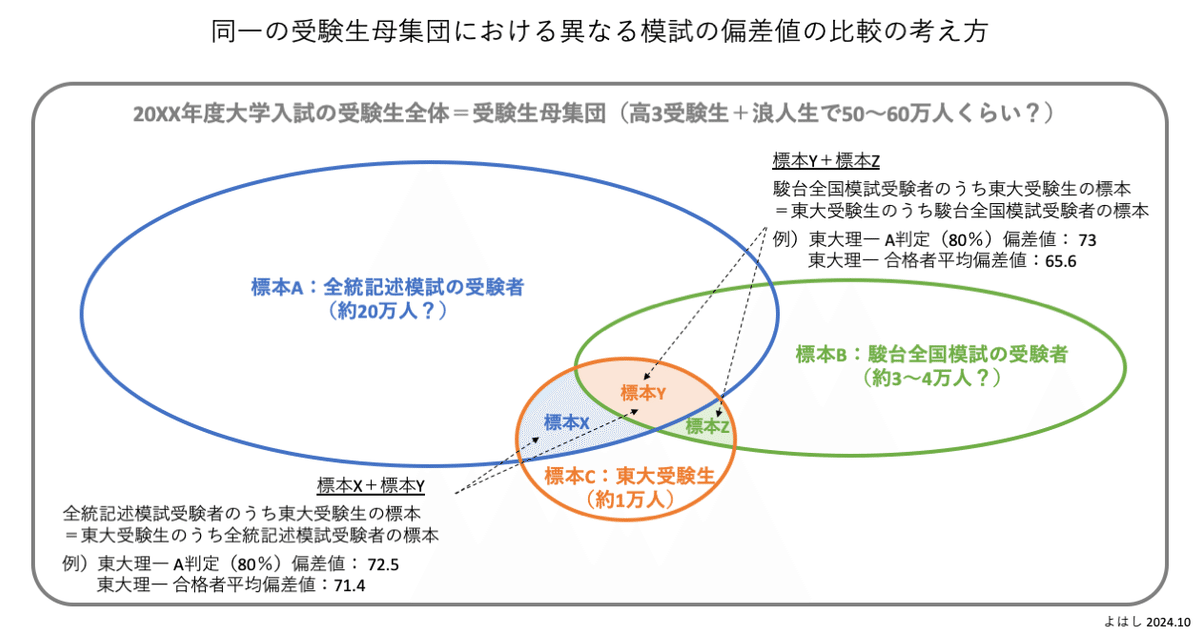
この場合の受験生母集団はグレー枠の20XX年度大学受験の受験生全体となります。この母集団の中、ブルー枠の全統記述模試の受験者の標本A、グリーン枠の駿台全国模試の受験者の標本Bとなります。並行して、この母集団の中にはオレンジ枠の東大受験生の標本Cが存在します。
この時、色を付けている標本X(ブルー)と標本Y(オレンジ)は、全統記述模試の標本Aの中で、東大を受験した標本です。同様に、標本Y(オレンジ)+標本Z(グリーン)は駿台全国模試の標本Bの中で、東大を受験した標本です。模試から見ると、X+YとY+Zは別の模試に属する標本となります。
一方、見方を変えて、東大受験者の標本Cから見てみます。すると、X+Yは東大受験者のうちの全統記述模試の受験者です。Y+Zは東大受験者のうちの駿台全国模試の受験者です。ここから考えると、東大受験者を母集団と見れば、X+Yはその標本であり、Y+Zもその標本となります。よって、東大受験者という同一の母集団の中で、X+YとY+Zは2つの標本として比較可能となります。
ここで、東大理一合格者の平均偏差値は、X+Yの全統記述模試では71.4、Y+Zの駿台全国模試では65.6でした。それぞれの標本に含まれる合格者の平均値は、東大合格者という母集団の中では、中心極限定理によって正規分布していると考えられます。
その際、2つの標本平均と母平均の差も正規分布も正規分布しています。そして、この標本平均と母平均の差は、①判定基準の違い、②総合偏差値の計算方法の違い、④模試受験者の学力レベルの違いに起因すると考えられるため、大学・学部・学科に依存しない定数となるはずです。
このような考え方で、大学・学部・学科の2つの模試の偏差値のデータを一定数集めて、回帰分析を行えば、その定数に①判定基準の違い、②総合偏差値の計算方法の違い、④模試受験者の学力レベルの違いが含まれて、母集団の違いを除去できると考えられます。
このロジックで、全統記述模試と駿台全国模試の偏差値変換をモデル化したのが、こちらの記事です。なお、回帰分析した際には、大学・学部・学科ごとに回帰予測値と実際値の間に残差が生じます。この残差は大学・学部・学科に固有の何かが影響しているものとして扱う必要があります。
◆異なる受験生母集団における異なる模試受験者の標本の比較
模試の偏差値比較ができない4つの要因のうち、3つを解消するロジックは考案できました。残る要因は③時間軸の違いです。具体的には、中学受験と高校受験と大学受験の模試をどう比較するかです。
基本的には時間軸が違うので、正面から考えると、異なる受験生母集団における模試は比較できません。ただ、逆に言えば、異なる受験生母集団においても、学力レベルが同等の標本を特定できれば、その標本が受験する模試の成績は同等のものとして扱えるはずです。
では、中学受験/高校受験/大学受験という異なる受験生母集団において、学力レベルが同等の標本とは何になるのでしょうか? パッと思いつくのは、大学の附属校です。早稲田大と附属高校と附属中学の3つの標本です。これを同等の学力とみなす考え方もブログや掲示板で見かけますが、同等の学力とみなす根拠がなく、ロジックとしては弱いです。
どうしたら同等の学力の標本を定義できるかを試行錯誤する中で思い至ったのが、早稲田と慶応の大学入試での合格者という標本です。早慶の合格者には東大併願の学力最上位層もいれば、MARCH本命で早慶にチャレンジしたら運良く合格した中上位層もいます。この早慶合格者内の学力分布は、東大合格者、早慶合格者、MARCH合格者などが混在する高校の学力分布に近い形になるはずです。
この考察をもう一歩進めると、早慶合格者の平均学力は、早慶進学者が学年中央値付近となる進学校の平均学力に等しくなると考えられます。それぞれで平均より上は早慶に合格しても東京一工などに合格して早慶には進学しない、平均付近は早慶に合格したらMARCHや他の国公立ではなく早慶に進学、平均より下は早慶に不合格でそれ以外に進学、という分布で概念的には一致するはずです。
つまり、大学入試における早慶合格者という標本、高校入試における早慶進学者が学年中央値の高校を集めた標本、中学入試における早慶進学者が学年中央値の中学を集めた標本、この3つの標本は同じ学力の標本と言えます。これを図示すると、このようになります。

右端が大学受験です。ブルー枠の標本Xが入試での早慶合格者です。厳密には指定校推薦とかも含まれますが、今回は一般入試と同じものとして扱います。そして、早慶合格者の枠の中に早慶進学者の標本xが含まれます。一方、早慶合格者の外にグリーンの附属校からの早慶進学者の標本Yが存在します。双方の進学者を合わせた色塗りの部分(標本x+標本Y)が全体の早慶進学者です。なお、附属校の標本Yは大学受験しないので、駿台全国模試の受験者には含まれない部分が大半となります。
中央の高校受験において、早慶進学が学年中央値となる高校を集めたのがオレンジ枠の標本Lです。この中には、大学入試で早慶に進学する標本xの水色部分が含まれます。中央のグリーン枠の標本Mは早慶附属高校の合格者で、この中の附属校進学者の大半が、大学進学時には早慶進学者である標本Yの一部分になります。下段のグリーン枠の標本Nは中学受験で早慶附属中学に入学して、そのまま早慶附属高校に内部進学する標本です。こちらは、高校受験を行わないので、駿台中学生テストの受験者には含まれません。
左端の中学受験でも、高校受験と同じ整理ができます。早慶進学が学年中央値となる中学を集めたのが、イエローの標本Aとなります。そして、早慶附属中の合格者が標本Bです。この中で附属中に進学したのが標本bで、これは高校進学時には標本Nになります。
この場合、中学受験の標本A(イエロー)、高校受験の標本L(オレンジ)、大学受験の標本X(ブルー)は、それぞれの標本平均が早慶合格者平均の同等の学力の標本と見なせます。そうなれば、この3つの標本のそれぞれの模試での平均偏差値を計算することで、中学受験と高校受験と大学受験の模試の偏差値の比較ができるはずです。このロジックで組み立てたのがこちらの記事となります。
4. 最後に
このように模試の間の偏差値を比較・変換するロジックを試行錯誤しながら検討して、到達したのが次の変換式です。
全統記述模試の偏差値が40〜70の範囲で、駿台全国模試(S) ≒ 全統記述模試(K)ー7
※二次回帰式では、S = 0.0191 x K^2 - 1.3153 x S + 62.076(R^2=0.9856)駿台全国模試の偏差値−3≒駿台中学生テストの偏差値≒SAPIXオープンの偏差値+α (αは1程度)
2つ目の変換式については、「SAPIXオープンは駿台全国模試や駿台中学生テストよりも偏差値が低く出るので、母集団は同等ではなくSAPIXオープンの方が上」という見解がネットでは一般論なのは承知しています。ただ、その一般論は合格80%偏差値で比較していることが多く、判定基準の違い(①)を取り除いた合格者平均偏差値で比較すると、SAPIXオープンの母集団(偏差値)は他の2つとほぼ同等か、上であっても+1程度というのが私の分析結果です。「SAPIXの中央値はMARCH」という言説と照らし合わせても、大きくはズレていないのではないかと考えます。
なお、上記はあくまで全体の比較・変換であり、個々の学校(学部・学科)で見ると誤差(残差)が存在します。
以上が偏差値比較の考察のまとめです。次回は冒頭に書いたように、「鉄緑会プレミアム」を計算してみようと思います。
